2020七年级数学下册 第一章 整式的乘除 1 3页

完全平方公式 课题 完全平方公式（1）‎ 课型 新授 教学目标 知识目标：‎ ‎1.完全平方公式的推导及其应用.‎ ‎2.完全平方公式的几何背景.‎ 能力目标：‎ ‎1.经历探索完全平方公式的过程，进一步发展符号感和推理能力.‎ ‎2.重视学生对算理的理解，有意识地培养他们有条理的思考和表达能力.‎ 情感目标：‎ ‎1.了解数学的历史，激发学习数学兴趣.‎ ‎2.鼓励学生自己探索算法的多样化，有意识地培养学生的创新能力.‎ 重点 会用完全平方公式进行简单的计算 难点 理解完全平方公式的结构特征，并灵活运用 教学用具 教学环节 说 明 二次备课 复习 ‎ （一）回顾思考 回顾平方差公式及其应该注意的问题，那么对吗？‎ 新课导入 ‎ （二）观察导入 ‎ 观察下列算式及其运算结果，你有什么发现？‎ ‎（m+3）2 （2+3x）2‎ ‎= (m+3)(m+3) =(2+3x)(2+3x)‎ ‎=m2+‎3m+‎3m+9 =4+2×3x+2×3x+9x2‎ ‎=m2+2×‎3m+9 =4+2×2×3x+9x2‎ ‎=m2+‎6m+9 =4+12x+9x2‎ ‎ 再举两例验证你的发现。‎ ‎ 发现：‎ 3‎ ‎（1）两个算式都是两个数和的平方，结果是三项，都有这两个数的平方；‎ ‎（2）算式都是两个数和的平方，结果是这两个数的平方和，再加上这两个数的乘积的2倍。‎ 课 程 讲 授 ‎（三）探索新知 ‎1.用式子表示这个规律：(a+b)2=a2+2ab+b2 ‎ 语言叙述：两数和的平方，等于它们的平方和加上它们的积的2倍。‎ ‎ 2.你能计算：(a－b)2 吗？‎ ‎ （1）：(a－b)2 = (a－b) (a－b)=a2－2ab+b2。‎ ‎ （2）(a－b)2=[a+(－b) ] 2=a2－‎2a(－b)+b2=a2－2ab+b2。‎ 一个是利用多项式的乘法，一个是利用公式，把差的形式化成了和的形式。用语言描述这个结果：两数差的平方，等于它们的平方和减去它们的积的2倍。我们把这个规律也当成公式，和前面的公式合起来称为完全平方公式。我们把(a+b)2=a2+2ab+b2称为和的完全平方公式，(a－b)2 =a2－2ab+b2称为差的完全平方公式。‎ ‎3. 再识完全平方公式 ‎（1） 结构特点：左边是二项式（两数和或差））的平方；右边是两数的平方和加上（或减去）这两数乘积的2倍。‎ ‎（2）两数和（或差）的平方，等于这两数的平方和加上（或减去）这两数积的2倍。‎ 口诀：首平方，尾平方，积的2倍放中央，是加是减看前方。‎ 这里的加减只是第一步的展开式要保持和前面的加减同步。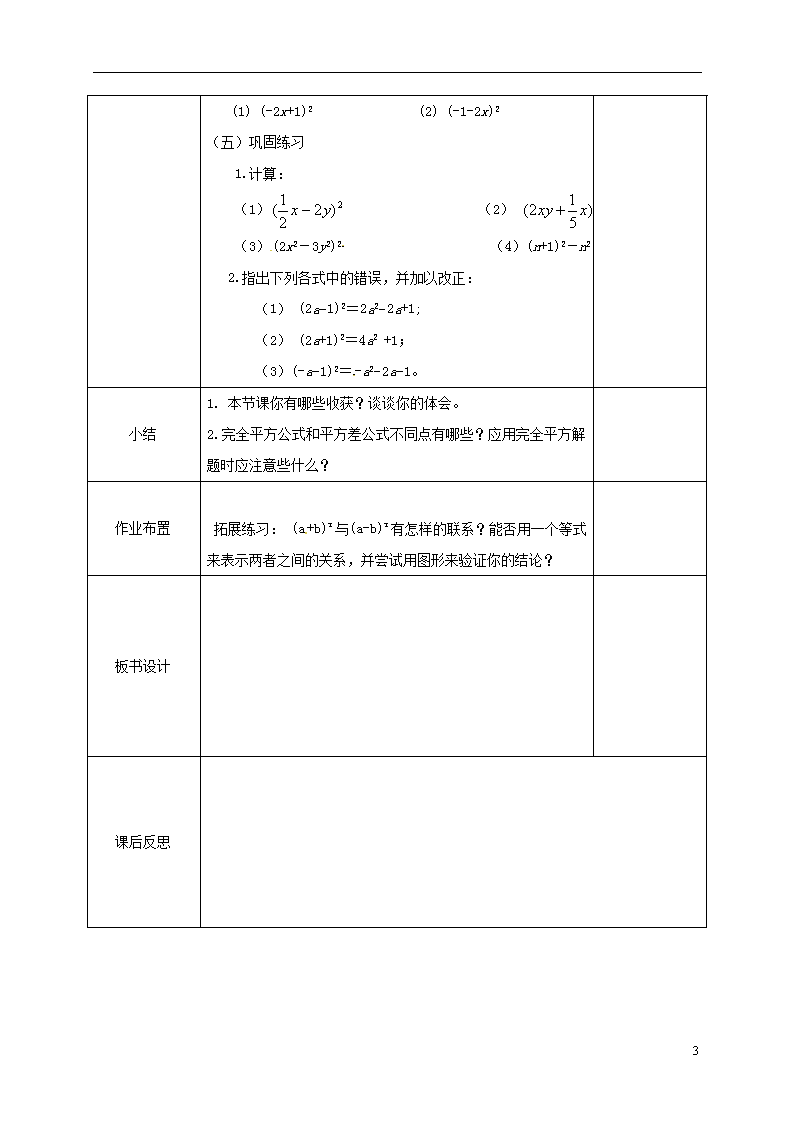（四）知识应用 例1 用完全平方公式计算：‎ ‎ （1）(2x−3)2 (2) (4x+5y)2 (3) (mn−a)2 ‎ 例2 利用完全平方公式计算：‎ 3‎ ‎(1) (-2x+1)2 (2) (-1-2x)2‎ ‎（五）巩固练习 ‎ 1.计算：‎ ‎（1） （2） ‎ ‎（3）(2x2－3y2)2 （4）(n+1)2－n2 ‎ ‎ 2.指出下列各式中的错误，并加以改正：‎ ‎ （1） (‎2a−1)2＝‎2a2−‎2a+1;‎ ‎ （2） (‎2a+1)2＝‎4a2 +1；‎ ‎ （3）(-a−1)2＝-a2−‎2a−1。‎ 小结 ‎1. 本节课你有哪些收获？谈谈你的体会。‎ ‎2. 完全平方公式和平方差公式不同点有哪些？应用完全平方解题时应注意些什么？ ‎ 作业布置 ‎ 拓展练习： (a+b)²与(a-b)²有怎样的联系？能否用一个等式来表示两者之间的关系，并尝试用图形来验证你的结论？‎ 板书设计 课后反思 3‎