七年级上数学课件- 3-1-2 等式的性质 课件（共16张PPT）_人教新课标 16页

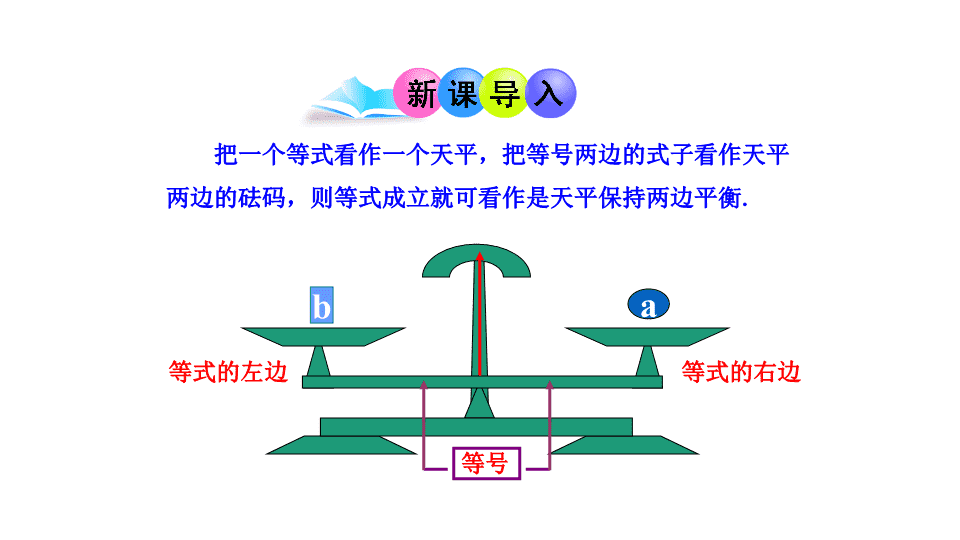
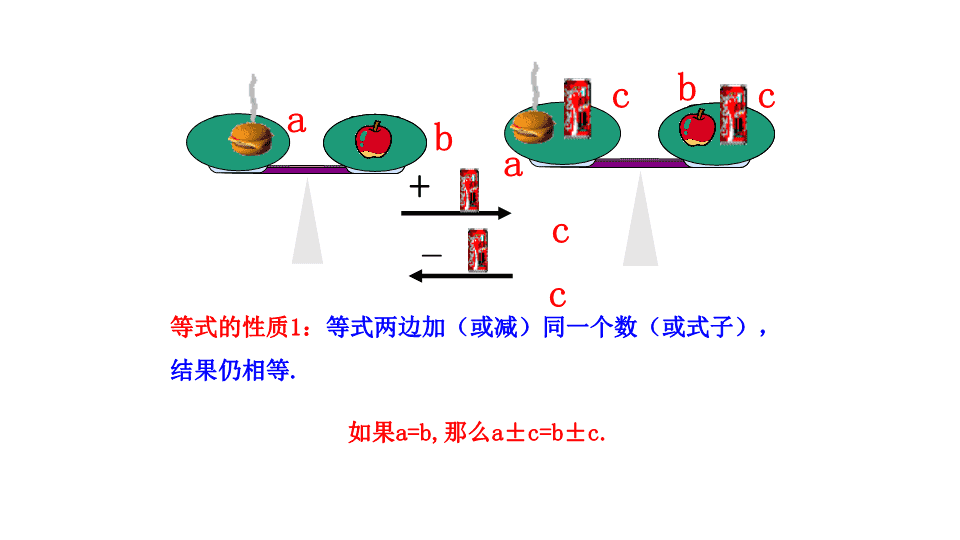
3.1.2 等式的性质 b a 把一个等式看作一个天平，把等号两边的式子看作天平 两边的砝码，则等式成立就可看作是天平保持两边平衡. 等式的左边 等式的右边 等号 + — 等式的性质1：等式两边加（或减）同一个数（或式子）， 结果仍相等. 如果a=b,那么a±c=b±c. c a b a b c cc 等式的性质2：等式两边乘同一个数,或除以同一个不为 0的数，结果仍相等. ×3 ÷3 ? ? 如果a=b,那么ac=bc. 如果a=b(c≠0),那么 a aa a bb bb a b.c c  a b a c b c.   如果 ，那么 【等式性质2】 a b ac bc. 如果 ，那么   a ba b c 0 , .c c   如果 　那么 【等式性质1】 注 意 1.等式两边都要参加运算，并且是作同一种运算.　　　　　　　　　　 2.等式两边加或减,乘或除以的数一定是同一个数 或同一个式子. 3.等式两边不能都除以0，即0不能作除数或分母. 若x=y，则下列等式是否成立，若成立，请指明依据等 式的哪条性质？若不成立，请说明理由. （1）x+ 5＝y+ 5 （2）x - a = y - a （3）（5－a）x＝（5－a）y （4） x y 5 a 5 a   成立，等式性质1 成立，等式性质1 成立，等式性质2 不一定成立，当a=5时等式两边都没 有意义. 思考 1.在下面的括号内填上适当的数或者代数式   xxx xx 2823 823  （2）∵ ∴      xxx xx 9989910 98910（3）∵ ∴ x2 x9 9    4662 462 x x （1）∵ ∴ 6 例1 利用等式的性质解下列方程： (1)x+7＝26 (2)3x＝2x-4 解：给等式两边同时减7， 得 x＋7－7＝26－7， 于是 x＝19 . 解：给等式两边减同时 减2x，得 3x－2x＝2x－2x－4， 于是 x＝－4. 1. 解方程: (1) x-3=-5 (2) -5x=4-6x 7 23 x x 15 5  （ ） x=-2 x=4 x=-1 例2 解方程：-4x＋8＝-5x-1. 解：给等式两边同时减8，得 -4x＋8－8＝-5x-1-8， -4x＝-5x-9， 给等式两边同时加5x，得 -4x+5x＝-5x+5x-9， x=-9. 例2 解方程：－4x＋8＝－5x －1 方程的解是否正确可以检验. 例如：把x=－9代入方程： 左边=－4×（－9）＋8=44； 右边=－5×（－9）－1＝44. 左边=右边 所以x＝-9是方程－4x＋8＝-5x -1 的解. 2.解方程并检验:-6x+3=2-7x. 解：两边减3，得 -6x＝-7x-1 两边加7x，得 x=-1 检验：把x=－1代入方程： 左边=－6×（－1）＋3=9； 右边=2－7×（－1）＝9. 左边=右边， 所以x＝-1是原方程的解. 1.填空，并在括号内注明利用了等式的哪条性 质. （1）如果5+x=4，那么x=____（ ） （2）如果-2x=6，那么x=____ ( ) 2.已知m+a=n+b，根据等式的性质变形为m=n, 那么a、b必须符合的条件是（ ） A.a=-b B. -a=b C.a=b D.a，b可以是任意 数 -1 等式的性质1 -3 等式的性质2 C 3.如果a=b, 且 则c应满足的条件是_________. 4.解方程 （1）4x - 2 = 2 （2） x + 2 = 6 a b c c  1 2 c≠0 x=1 x=8 5.观察下列变形，并回答问题： 3ａ+ｂ-2 ＝2ａ+ｂ-2 3ａ+ｂ＝2ａ+ｂ 第一步 　 3ａ＝2ａ 第二步 　　 3＝2 第三步 上述变形是否正确？若不正确，请指明错在哪一步？原 因是什么？怎么改正？ 解：不正确.错在第三步，两边同除以a时，不能保证a不等 于0. 改正：两边同时减2a,得a=0. 本节课我们学习了： 1.等式的性质，并运用性质进行等式变形. 2.运用等式的性质解简单的方程. 3.对方程的解进行检验.