第六章第21课时6立方根 4页

‎6 ．3实数（第1课时）‎ 一、学习目标：‎ ‎1、了解实数的意义，能对实数按要求进行分类。‎ ‎2、了解实数范围内，相反数、倒数、绝对值的意义。‎ ‎3、了解数轴上的点与实数一一对应，能用数轴上的点来表示无理数。‎ 二、重点与难点 学习重点：理解实数的概念。‎ 学习难点：正确理解实数的概念。‎ 三、 合作探究 ‎（一）学前准备 ‎1、填空：（有理数的两种分类）‎ 有理数 有理数 ‎ ‎ 2、 使用计算器计算，把下列有理数写成小数的形式，你有什么发现？‎ ‎ 3 ， ， ， ， ，‎ ‎（二）、探究新知 ‎1、归纳： 任何一个有理数都可以写成_______小数或________小数的形式。反过来，任何______小数或____________小数也都是有理数 观察 通过前面的探讨和学习，我们知道，很多数的_____根和______根都是____________小数， ____________小数又叫无理数，也是无理数 结论： _______和_______统称为实数 你能举出一些无理数吗？‎ ‎2、试一试 把实数分类 ‎ ‎ 像有理数一样，无理数也有正负之分。例如，，是____无理数，，，是____无理数。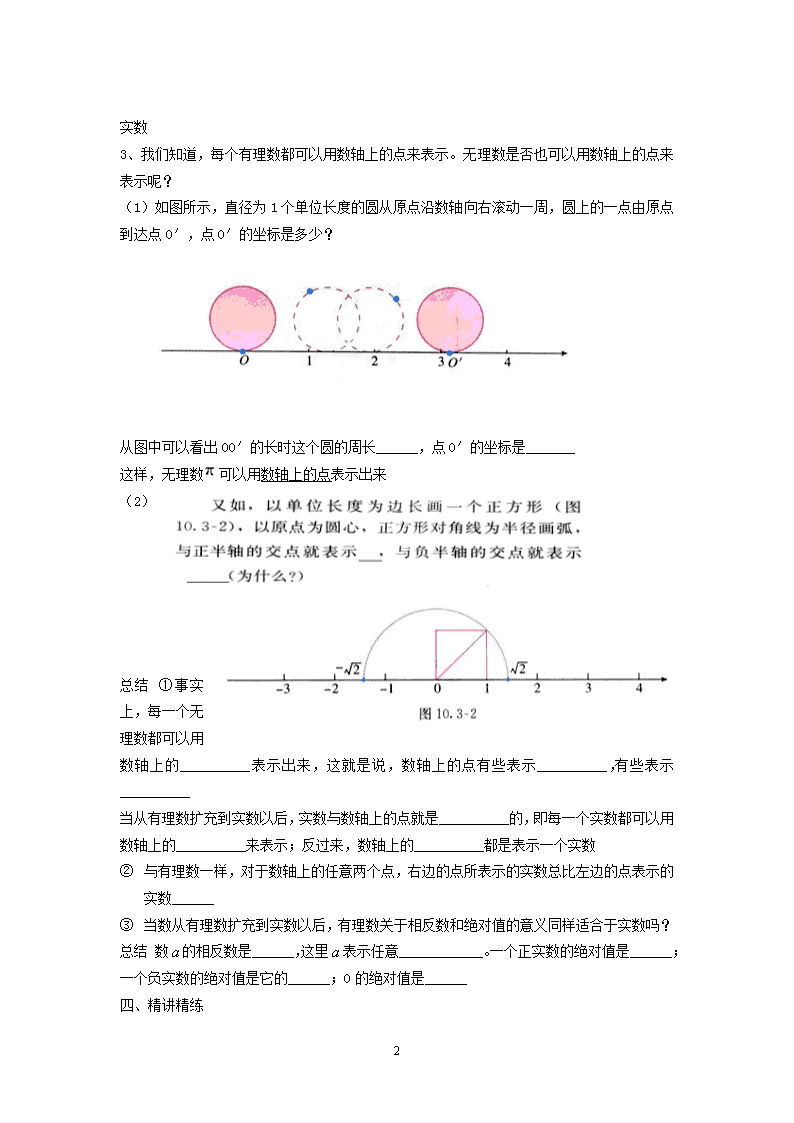由于非0有理数和无理数都有正负之分，所以实数也可以这样分类：‎ 4‎ ‎ ‎ ‎ ‎ 实数 ‎3、我们知道，每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点来表示呢？‎ ‎（1）如图所示，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点到达点O′，点O′的坐标是多少？‎ 从图中可以看出OO′的长时这个圆的周长______，点O′的坐标是_______‎ 这样，无理数可以用数轴上的点表示出来 ‎（2）‎ 总结 ①事实上，每一个无理数都可以用数轴上的__________表示出来，这就是说，数轴上的点有些表示__________，有些表示__________‎ 当从有理数扩充到实数以后，实数与数轴上的点就是__________的，即每一个实数都可以用数轴上的__________来表示；反过来，数轴上的__________都是表示一个实数 ② 与有理数一样，对于数轴上的任意两个点，右边的点所表示的实数总比左边的点表示的实数______‎ ③ 当数从有理数扩充到实数以后，有理数关于相反数和绝对值的意义同样适合于实数吗？‎ 总结 数的相反数是______，这里表示任意____________。一个正实数的绝对值是______；一个负实数的绝对值是它的______；0的绝对值是______‎ 四、 精讲精练 4‎ ‎ ‎ 例1、把下列各数分别填入相应的集合里：‎ ‎ ‎ 正有理数{ } ‎ 负有理数{ }‎ 正无理数{ } ‎ 负无理数{ }‎ ‎2、下列实数中是无理数的为（ ）A. 0 B. C. D. ‎ ‎3、 的相反数是 ，绝对值 ‎ ‎4、绝对值等于 的数是 ， 的平方是 ‎ ‎5、‎ ‎6、求绝对值 练习 ‎(一)、判断下列说法是否正确：‎ ‎1.实数不是有理数就是无理数。 （ ）‎ ‎2.无限小数都是无理数。 （ ）‎ ‎3.无理数都是无限小数。 （ ）‎ ‎4.带根号的数都是无理数。 （ ） ‎ ‎5.两个无理数之和一定是无理数。 （ ）‎ ‎6.所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。（ ）‎ ‎(二)、填空1、 ‎ ‎2、‎ ‎3、比较大小 ‎ ‎4、_________‎ 四、 课堂小结 ‎ ‎ 这节课你有什么新发现？知道了哪些新知识？‎ 4‎ ‎ ‎ 无理数的特征:‎ ‎1．圆周率及一些含有的数 ‎ ‎2．开不尽方的数 ‎3．无限不循环小数 注意:带根号的数不一定是无理数 四、 作业 ‎1、 把下列各数填入相应的集合内：‎ 有理数集合{ } 无理数集合{ }‎ 整数集合{ } 分数集合{ }‎ 实数集合{ }‎ ‎2、下列各数中，是无理数的是（ ）A. B. C. D. ‎ ‎3、已知四个命题，正确的有（ ）‎ ‎⑴有理数与无理数之和是无理数 ⑵有理数与无理数之积是无理数 ‎⑶无理数与无理数之积是无理数 ⑷无理数与无理数之积是无理数 A. 1个 B. 2个 C. 3个 D.4个 ‎4、若实数满足，则（ ）‎ A. B. C. D. ‎ ‎5、下列说法正确的有（ ）‎ ‎⑴不存在绝对值最小的无理数 ⑵不存在绝对值最小的实数 ‎⑶不存在与本身的算术平方根相等的数 ⑷比正实数小的数都是负实数 ‎⑸非负实数中最小的数是0‎ A. 2个 B. 3个 C. 4个 D.5个 ‎6、⑴的相反数是_________ ，绝对值是_________ ‎ ‎ ‎ ‎⑵ ⑶若，则 _________‎ ‎⑷_______‎ ‎7、是实数，则_________ ‎ ‎ ‎ 4‎ ‎ ‎