七年级上第一次月考试卷 (2) 13页

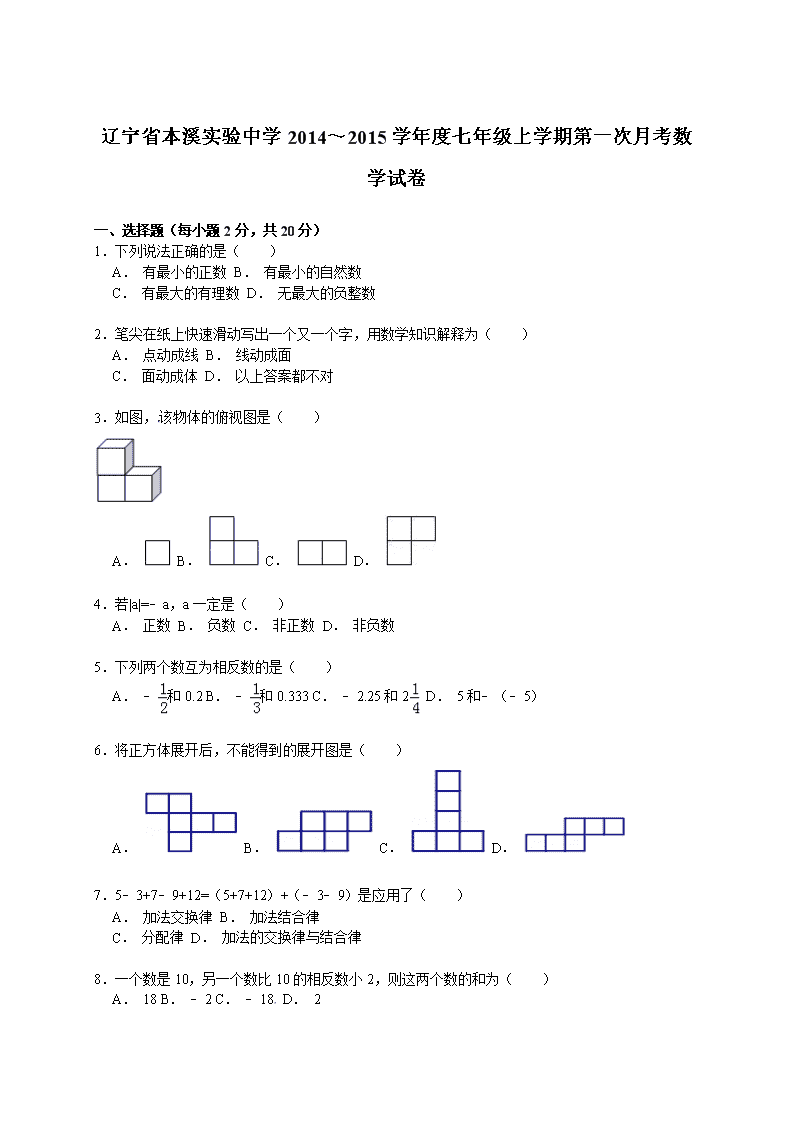
辽宁省本溪实验中学2014～2015学年度七年级上学期第一次月考数学试卷 ‎　‎ 一、选择题（每小题2分，共20分）‎ ‎1．下列说法正确的是（　　）‎ ‎　 A． 有最小的正数 B． 有最小的自然数 ‎　 C． 有最大的有理数 D． 无最大的负整数 ‎　‎ ‎2．笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为（　　）‎ ‎　 A． 点动成线 B． 线动成面 ‎　 C． 面动成体 D． 以上答案都不对 ‎　‎ ‎3．如图，该物体的俯视图是（　　）‎ ‎　 A． B． C． D． ‎ ‎　‎ ‎4．若|a|=﹣a，a一定是（　　）‎ ‎　 A． 正数 B． 负数 C． 非正数 D． 非负数 ‎　‎ ‎5．下列两个数互为相反数的是（　　）‎ ‎　 A． ﹣和0.2 B． ﹣和0.333 C． ﹣2.25和2 D． 5和﹣（﹣5）‎ ‎　‎ ‎6．将正方体展开后，不能得到的展开图是（　　）‎ ‎　 A． B． C． D． ‎ ‎　‎ ‎7．5﹣3+7﹣9+12=（5+7+12）+（﹣3﹣9）是应用了（　　）‎ ‎　 A． 加法交换律 B． 加法结合律 ‎　 C． 分配律 D． 加法的交换律与结合律 ‎　‎ ‎8．一个数是10，另一个数比10的相反数小2，则这两个数的和为（　　）‎ ‎　 A． 18 B． ﹣2 C． ﹣18 D． 2‎ ‎　‎ ‎9．正方体的截面不可能是（　　）‎ ‎　 A． 四边形 B． 五边形 C． 六边形 D． 七边形 ‎　‎ ‎10．如图，数轴上点P表示的数可能是（　　）‎ ‎　 A． ﹣2.66 B． ﹣3.57 C． ﹣3.2 D． ﹣1.89‎ ‎　‎ ‎　‎ 二、填空题（每小题2分，共20分）‎ ‎11．如图所示，电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面，则：‎ A图象是　　　　　　号摄像机所拍，‎ B图象是　　　　　　号摄像机所拍，‎ C图象是　　　　　　号摄像机所拍，‎ D图象是　　　　　　号摄像机所拍．‎ ‎　‎ ‎12．﹣的绝对值是　　　　　　，相反数是　　　　　　．‎ ‎　‎ ‎13．在数轴上A点到原点的距离等于3个单位长，B点到A点的距离等于5个单位长，则B点所表示的数到原点的距离为　　　　　　．‎ ‎　‎ ‎14．|x+3|+|y﹣2|=0，则x﹣y=　　　　　　．‎ ‎　‎ ‎15．如图所示，截去正方体一角变成一个多面体，这个多面体有　　　　　　个面，有　　　　　　条棱，有　　　　　　个顶点．‎ ‎　‎ ‎16．若要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为6，x=　　　　　　，y=　　　　　　．‎ ‎　‎ ‎17．若向南走2m记作﹣2m，则向北走3m，记作　　　　　　m．‎ ‎　‎ ‎18．绝对值大于2且不大于4的所有整数是　　　　　　．‎ ‎　‎ ‎19．有理数中，最大的负整数是　　　　　　，绝对值最小的数是　　　　　　．‎ ‎　‎ ‎20．观察下面的一列数：，﹣，，﹣…请你找出其中排列的规律，并按此规律填空．第5个数是　　　　　　，第10个数是　　　　　　．‎ ‎　‎ ‎　‎ 三、解答题（共6小题）‎ ‎21．把下列各数序号分别填在表示它所在的集合里：‎ ‎①﹣5，②﹣，③2004，④﹣（﹣4），⑤，⑥﹣|﹣1|，⑦﹣0.36，⑧0，⑨6.2，⑩‎ ‎（1）正整数集合{　　　　　　…}‎ 负数集合{　　　　　　…}‎ ‎（3）整数集合{　　　　　　…}‎ ‎（4）分数集合{　　　　　　…}．‎ ‎　‎ ‎22．化简：‎ ‎（1）﹣{+[﹣（+3）]}； ‎ ‎﹣{﹣[﹣（﹣|﹣3|）}．‎ ‎　‎ ‎23．（1）比较有理数的大小：‎ ‎﹣与﹣‎ 在数轴上表示下列各数，并把它们用“＜”号连接起来 ‎2.5，﹣（﹣1），+（﹣4），﹣1，﹣（+3），0．‎ ‎　‎ ‎24．计算下列各题：‎ ‎（1）（﹣12）﹣5+（﹣14）﹣（﹣39）‎ ‎3+（﹣）﹣（﹣）+2‎ ‎（3）2﹣5+4﹣（﹣7）+9﹣6）‎ ‎（4）（﹣1）﹣（+6）﹣2.25+‎ ‎（5）﹣+（﹣）﹣‎ ‎（6）（﹣3）﹣（﹣1.5）﹣（﹣3）+（+3.5）‎ ‎（7）﹣3﹣（﹣4）+（﹣6）﹣3‎ ‎（8）1﹣2+3﹣4+5﹣6+7﹣…﹣98+99﹣100．‎ ‎　‎ ‎25．如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数．请你画出它的主视图与左视图．‎ ‎　‎ ‎26．十一黄金周期间，花果山7天中每天旅游人数的变化情况如下表（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：‎ 日期 1日 2日 3日 4日 5日 6日 7日 人数变化/万人 +0.5 +0.7 +0.8 ﹣0.4 ﹣0.6 +0.2 ﹣0.1‎ ‎（1）请判断7天内游客人数量最多和最少的各是哪一天？它们相差多少万人？‎ 如果9月30日旅游人数为2万人，平均每人消费300元，请问风景区在此7天内总收入为多少万元？‎ ‎　‎ ‎　‎ 辽宁省本溪实验中学2014～2015学年度七年级上学期第一次月考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（每小题2分，共20分）‎ ‎1．下列说法正确的是（　　）‎ ‎　 A． 有最小的正数 B． 有最小的自然数 ‎　 C． 有最大的有理数 D． 无最大的负整数 考点： 有理数．‎ 分析： 根据有理数的分类，利用排除法求解．‎ 解答： 解：既没有最大的也没有最小的正数，A错误；‎ 最小的自然数是0，B正确；‎ 有理数既没有最大也没有最小，C错误；‎ 最大的负整数是﹣1，D错误；‎ 故选B．‎ 点评： 本题主要考查有理数既没有最大也没有最小，但有最小的自然数是0．‎ ‎　‎ ‎2．笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为（　　）‎ ‎　 A． 点动成线 B． 线动成面 ‎　 C． 面动成体 D． 以上答案都不对 考点： 点、线、面、体．‎ 分析： 利用点动成线，线动成面，面动成体，进而得出答案．‎ 解答： 解：笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为点动成线．‎ 故选：A．‎ 点评： 此题主要考查了点、线、面、体，正确把握它们之间的关系是解题关键．‎ ‎　‎ ‎3．如图，该物体的俯视图是（　　）‎ ‎　 A． B． C． D． ‎ 考点： 简单组合体的三视图．‎ 分析： 从上面看到的图叫做俯视图，根据图中正方体摆放的位置判定则可．‎ 解答： 解：从上面看，是横放两个正方体．‎ 故选C．‎ 点评： 本题考查了三视图的知识，俯视图是从物体的上面看得到的视图，解答时学生易将三种视图混淆而错误的选其它选项．‎ ‎　‎ ‎4．若|a|=﹣a，a一定是（　　）‎ ‎　 A． 正数 B． 负数 C． 非正数 D． 非负数 考点： 绝对值．‎ 分析： 根据负数的绝对值等于他的相反数，可得答案．‎ 解答： 解：∵非正数的绝对值等于他的相反数，|a|=﹣a，‎ a一定是非正数，‎ 故选：C．‎ 点评： 本题考查了绝对值，注意负数的绝对值等于他的相反数．‎ ‎　‎ ‎5．下列两个数互为相反数的是（　　）‎ ‎　 A． ﹣和0.2 B． ﹣和0.333 C． ﹣2.25和2 D． 5和﹣（﹣5）‎ 考点： 相反数．‎ 分析： 此题依据相反数的概念作答．相反数的定义：只有符号不同的两个数互为相反数，0的相反数是0．‎ 解答： 解：A、﹣的相反数是，错误；‎ B、﹣的相反数的是，错误；‎ C、﹣2.25和2互为相反数，正确；‎ D、5的相反数是﹣5，5=﹣（﹣5），错误．‎ 故选：C．‎ 点评： 此题关键是看两个数是否“只有符号不同”，并注意分数与小数的转化．‎ ‎　‎ ‎6．将正方体展开后，不能得到的展开图是（　　）‎ ‎　 A． B． C． D． ‎ 考点： 几何体的展开图．‎ 分析： 根据正方体的平面展开图的特征，图形中出现“田”字的不是正方体的展开图．‎ 解答： 解：选项A、C、D都能折叠成正方体，只有选项B中，出现“田”字形，不能折成正方体．‎ 故选：B．‎ 点评： 此题主要考查了几何体的展开图，熟练掌握正方体展开图的特征是解决此类问题的关键．‎ ‎　‎ ‎7．5﹣3+7﹣9+12=（5+7+12）+（﹣3﹣9）是应用了（　　）‎ ‎　 A． 加法交换律 B． 加法结合律 ‎　 C． 分配律 D． 加法的交换律与结合律 考点： 有理数的加法．‎ 分析： 本题需先根据加法的交换律、加法的结合律等知识点进行判断，即可求出答案．‎ 解答： 解：根据意义得：5﹣3+7﹣9+12=（5+7+12）+（﹣3﹣9），‎ 故用了加法的交换律与结合律．‎ 故选D．‎ 点评： 本题主要考查了有理数的加法，在解题时要根据加法的交换律、加法的结合律等知识点进行判断是本题的关键．‎ ‎　‎ ‎8．一个数是10，另一个数比10的相反数小2，则这两个数的和为（　　）‎ ‎　 A． 18 B． ﹣2 C． ﹣18 D． 2‎ 考点： 有理数的减法；相反数；有理数的加法．‎ 分析： 先根据相反数的概念求出10的相反数，再根据有理数的减法求出比10的相反数小2，再把两数相加即可．‎ 解答： 解：∵10的相反数是﹣10，‎ ‎∴比10的相反数小2是﹣12，‎ ‎∴这两个数的和为10+（﹣12）=﹣2．‎ 故选B．‎ 点评： 解答此题的关键是熟知相反数的概念及有理数的加减法则．‎ ‎　‎ ‎9．正方体的截面不可能是（　　）‎ ‎　 A． 四边形 B． 五边形 C． 六边形 D． 七边形 考点： 截一个几何体．‎ 分析： 用平面去截正方体，得的截面可能为三角形、四边形、五边形、六边形，据此判断即可．‎ 解答： 解：用平面去截正方体，得的截面可能为三角形、四边形、五边形、六边形，不可能为七边形，故选D．‎ 点评： 本题考查正方体的截面．正方体有六个面，截面与其六个面相交最多得六边形，不可能是七边形或多于七边的图形．‎ ‎　‎ ‎10．如图，数轴上点P表示的数可能是（　　）‎ ‎　 A． ﹣2.66 B． ﹣3.57 C． ﹣3.2 D． ﹣1.89‎ 考点： 数轴；绝对值；有理数大小比较．‎ 专题： 推理填空题．‎ 分析： 先根据数轴得出P点表示的数的范围，再根据有理数的大小比较法则尽判断即可．‎ 解答： 解：设P表示的数是x，‎ 由数轴可知：P点表示的数大于﹣3，且小于﹣2，即﹣3＜x＜﹣2，‎ A、﹣3＜﹣2.66＜﹣2，故本选项正确；‎ B、﹣3.57＜﹣3，故本选项错误；‎ C、﹣3.2＜﹣3，故本选项错误；‎ D、﹣2＜﹣1.89，故本选项错误；‎ 故选A．‎ 点评： 本题考查了学生的观察图形的能力和辨析能力，注意：两个负数比较大小，其绝对值大的反而小，在数轴上左边的数比右边的数大．‎ ‎　‎ 二、填空题（每小题2分，共20分）‎ ‎11．如图所示，电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面，则：‎ A图象是　2　号摄像机所拍，‎ B图象是　3　号摄像机所拍，‎ C图象是　4　号摄像机所拍，‎ D图象是　1　号摄像机所拍．‎ 考点： 简单组合体的三视图．‎ 分析： 1号机正对壶柄，为D图形；‎ ‎2号机看到的壶柄在右边，为A图形；‎ ‎3号机的位置看不到壶柄，为B图形；‎ ‎4号机看到的壶柄在左边，为C图形．‎ 解答： 解：根据4个机器的不同位置可得到A图象是2号摄像机所拍，B图象是3号摄像机所拍，C图象是4号摄像机所拍，D图象是1号摄像机所拍．‎ 点评： 解决本题的关键是抓住拍摄物体的一个特征得到位于不同位置所得到的不同图形．‎ ‎12．﹣的绝对值是　　，相反数是　　．‎ 考点： 绝对值；相反数．‎ 分析： 根据绝对值的性质和相反数的定义解答即可．‎ 解答： 解：﹣的绝对值是，相反数是．‎ 故答案为：；．‎ 点评： 本题考查了绝对值的性质，相反数的定义，一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．‎ ‎　‎ ‎13．在数轴上A点到原点的距离等于3个单位长，B点到A点的距离等于5个单位长，则B点所表示的数到原点的距离为　8或2　．‎ 考点： 数轴．‎ 分析： 先求出A、B两点所表示的数，再根据各点到原点距离的定义解答即可．‎ 解答： 解：∵数轴上A点到原点的距离等于3个单位长，‎ ‎∴点A表示﹣3或3．‎ ‎∵B点到A点的距离等于5个单位长，‎ ‎∴当点A表示﹣3时，|﹣3﹣B|=5，解得B=﹣8或B=2；‎ 当点A表示3时，|3﹣B|=5，解得B=﹣2或B=8．‎ ‎∵|±8|=8，|±2|=2，‎ ‎∴B点所表示的数到原点的距离，8或2．‎ 故答案为：8或2．‎ 点评： 本题考查的是数轴，根据题意画出图形，利用数形结合求解是解答此题的关键．‎ ‎　‎ ‎14．|x+3|+|y﹣2|=0，则x﹣y=　﹣5　．‎ 考点： 非负数的性质：绝对值；有理数的减法．‎ 分析： 根据非负数的性质列式求出x、y的值，然后代入代数式进行计算即可得解．‎ 解答： 解：由题意得，x+3=0，y﹣2=0，‎ 解得x=﹣3，y=2，‎ 所以，x﹣y=﹣3﹣2=﹣5．‎ 故答案为：﹣5．‎ 点评： 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．‎ ‎　‎ ‎15．如图所示，截去正方体一角变成一个多面体，这个多面体有　7　个面，有　12　条棱，有　7　个顶点．‎ 考点： 截一个几何体；认识立体图形．‎ 分析： 截去正方体一角变成一个多面体，这个多面体多了一个面、棱不变，少了一个顶点．‎ 解答： 解：仔细观察图形，正确地数出多面体的面数、棱数及顶点数，它们分别是7，12，7．‎ 点评： 本题结合截面考查多面体的相关知识．对于一个多面体：顶点数+面数﹣棱数=2．‎ ‎　‎ ‎16．若要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为6，x=　5　，y=　3　．‎ 考点： 专题：正方体相对两个面上的文字．‎ 专题： 数形结合．‎ 分析： 利用正方体及其表面展开图的特点解题．‎ 解答： 解：这是一个正方体的平面展开图，共有六个面，其中面“1”与面“x”相对，面“3”与面“y”相对．‎ 因为相对面上两个数之和为6，所以，x=5，y=3．‎ 故答案为：5，3．‎ 点评： 注意正方体的空间图形，从相对面入手，分析及解答问题．‎ ‎　‎ ‎17．若向南走2m记作﹣2m，则向北走3m，记作　+3　m．‎ 考点： 正数和负数．‎ 专题： 应用题．‎ 分析： 在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．‎ 解答： 解：“正”和“负”相对，所以，向南走2m记作﹣2m，则向北走3m记作+3m．‎ 点评： 解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．‎ ‎　‎ ‎18．绝对值大于2且不大于4的所有整数是　﹣4，﹣3，3，4　．‎ 考点： 绝对值．‎ 分析： 根据绝对值的意义，可得答案．‎ 解答： 解：绝对值大于2且不大于4的所有整数是﹣4，﹣3，3，4，‎ 故答案为：﹣4，﹣3，3，4．‎ 点评： 本题考查了绝对值，注意绝对值不大于4的意思是可以等于4．‎ ‎　‎ ‎19．有理数中，最大的负整数是　﹣1　，绝对值最小的数是　0　．‎ 考点： 绝对值．‎ 分析： 根据有理数的定义和绝对值的性质直接求解．‎ 解答： 解：有理数中，最大的负整数是﹣1，绝对值最小的数是0．‎ 点评： 考查绝对值的性质，0的绝对值是0．‎ ‎　‎ ‎20．观察下面的一列数：，﹣，，﹣…请你找出其中排列的规律，并按此规律填空．第5个数是　　，第10个数是　﹣　．‎ 考点： 规律型：数字的变化类．‎ 分析： 由=，﹣=﹣，=，﹣=…可以发现分子永远为1，分母是两个相邻数的成积，且其中一个为项的序号，奇数项永远为正数，偶数项永远为负数，由此规律推出第5个数和第10个数．‎ 解答： 解：∵=，﹣=﹣，=，﹣=…‎ ‎∴第5个数是=，第10个数是﹣=﹣．‎ 故答案为：；﹣．‎ 点评： 此题主要考查了数字变化规律，通过原来一列数的等价变换，得出各项的变化规律及由变化写出求任意一项时的规律式是解题关键．‎ ‎　‎ 三、解答题（共6小题）‎ ‎21．把下列各数序号分别填在表示它所在的集合里：‎ ‎①﹣5，②﹣，③2004，④﹣（﹣4），⑤，⑥﹣|﹣1|，⑦﹣0.36，⑧0，⑨6.2，⑩‎ ‎（1）正整数集合{　③，④　…}‎ 负数集合{　①，②，⑥，⑦　…}‎ ‎（3）整数集合{　①，③，④，⑥，⑧　…}‎ ‎（4）分数集合{　②，⑤，⑦，⑨　…}．‎ 考点： 有理数．‎ 分析： （1）根据大于零的整数是正整数，可得正整数集合；‎ 根据小于零的数是负数，可得负数集合；‎ ‎（3）根据分母为一的数是整数，可得整数集合；‎ ‎（4）根据分母不为一的数是分数，可得分数集合．‎ 解答： 解：（1）正整数集合{ ③，④…}‎ 负数集合{ ①，②，⑥，⑦…}‎ ‎（3）整数集合{ ①，③，④，⑥，⑧…}‎ ‎（4）分数集合{ ②，⑤，⑦，⑨…}．‎ 点评： 本题考查了有理数，大于零的数是正数，小于零的数是负数，分母为一的数是整数，分母不为一的数是分数．‎ ‎　‎ ‎22．化简：‎ ‎（1）﹣{+[﹣（+3）]}； ‎ ‎﹣{﹣[﹣（﹣|﹣3|）}．‎ 考点： 相反数．‎ 分析： 根据只有符号不同的两个数互为相反数，可得一个数的相反数．‎ 解答： 解：（1）原式=﹣{+[﹣3]}=﹣{﹣3}=3；‎ 原式=﹣{﹣[﹣（﹣3）]}=﹣{﹣[+3]}=﹣{﹣3}=3．‎ 点评： 本题考查了相反数，去小括号、中括号、大括号的顺序，得出答案．‎ ‎　‎ ‎23．（1）比较有理数的大小：‎ ‎﹣与﹣‎ 在数轴上表示下列各数，并把它们用“＜”号连接起来 ‎2.5，﹣（﹣1），+（﹣4），﹣1，﹣（+3），0．‎ 考点： 有理数大小比较；数轴．‎ 分析： （1）直接利用有理数比较大小的方法得出即可；‎ 首先将各数在数轴上表示，进而再比较大小即可．‎ 解答： 解：（1）∵|﹣|=，|﹣|=，‎ ‎∴＞，‎ ‎∴﹣＜﹣；‎ 如图所示：‎ ‎+（﹣4）＜﹣（+3）＜﹣1＜0＜﹣（﹣1）＜2.5．‎ 点评： 此题主要考查了有理数比较大小，利用数形结合得出是解题关键．‎ ‎　‎ ‎24．计算下列各题：‎ ‎（1）（﹣12）﹣5+（﹣14）﹣（﹣39）‎ ‎3+（﹣）﹣（﹣）+2‎ ‎（3）2﹣5+4﹣（﹣7）+9﹣6）‎ ‎（4）（﹣1）﹣（+6）﹣2.25+‎ ‎（5）﹣+（﹣）﹣‎ ‎（6）（﹣3）﹣（﹣1.5）﹣（﹣3）+（+3.5）‎ ‎（7）﹣3﹣（﹣4）+（﹣6）﹣3‎ ‎（8）1﹣2+3﹣4+5﹣6+7﹣…﹣98+99﹣100．‎ 考点： 有理数的加减混合运算．‎ 专题： 计算题．‎ 分析： （1）原式利用减法法则变形，计算即可得到结果；‎ 原式利用减法法则变形，计算即可得到结果；‎ ‎（3）原式利用减法法则变形，计算即可得到结果；‎ ‎（4）原式结合后，相加即可得到结果；‎ ‎（5）原式结合后，相加即可得到结果；‎ ‎（6）原式利用减法法则变形，计算即可得到结果；‎ ‎（7）原式利用减法法则变形，计算即可得到结果；‎ ‎（8）原式结合后，相加即可得到结果．‎ 解答： 解：（1）原式=﹣12﹣5﹣14+39=﹣31+39=8；‎ 原式=3﹣++2=3+3=6；‎ ‎（3）原式=2﹣5+4+7+9﹣6=2；‎ ‎（4）原式=﹣1﹣6﹣2.25+3=﹣4+3=﹣1；‎ ‎（5）原式=﹣﹣﹣==﹣；‎ ‎（6）原式=﹣3+1.5+3+3.5=5；‎ ‎（7）原式=﹣3+4﹣6﹣3=﹣9=﹣9；‎ ‎（8）原式=（1﹣2）+（3﹣4）+…+（99﹣100）=﹣1﹣1…﹣1=﹣50．‎ 点评： 此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎25．如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数．请你画出它的主视图与左视图．‎ 考点： 作图-三视图；由三视图判断几何体．‎ 分析： 主视图有3列，每列小正方形数目分别为3，2，4；左视图有3列，每列小正方形数目分别为2，3，4．依此画出图形即可求解．‎ 解答： 解：如图所示：‎ 点评： 本题考查实物体的三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．本题画几何体的三视图时应注意小正方形的数目及位置．‎ ‎　‎ ‎26．十一黄金周期间，花果山7天中每天旅游人数的变化情况如下表（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：‎ 日期 1日 2日 3日 4日 5日 6日 7日 人数变化/万人 +0.5 +0.7 +0.8 ﹣0.4 ﹣0.6 +0.2 ﹣0.1‎ ‎（1）请判断7天内游客人数量最多和最少的各是哪一天？它们相差多少万人？‎ 如果9月30日旅游人数为2万人，平均每人消费300元，请问风景区在此7天内总收入为多少万元？‎ 考点： 正数和负数．‎ 分析： （1）比较统计表中的数据，即可得出旅游人数最多的是哪天，最少的是哪天，以及它们相差多少万人；‎ 算出黄金周期间的总人数，再乘以60就是总收入．最多一天有出游人数3万人，即：a+2.8=3万，可得出a的值．‎ 解答： 解：（1）游客人数量最多的是3日，最少的是5日，相差1.4万人；‎ ‎0.5+0.7+0.8﹣0.4﹣0.6+0.2﹣0.1=1.1（万人），‎ ‎300×（7×2+1.1）=4530（万元）．‎ 即风景区在此7天内总收入为4530万元．‎ 点评： 考查了正数和负数，解题关键是要读懂题目的意思，根据题目给出的条件，列式计算，注意单位的统一．‎