图形的旋转教案1 4页

‎ ‎ ‎10.3.1 图形的旋转 学习目标：‎ ‎（1）了解生活中旋转现象的广泛存在.（2）掌握旋转的有关概念，理解旋转变换也是图形的一种基本变换.（3）会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋转角.（4）理解图形的旋转变换是由旋转中心、旋转角和旋转方向所决定的，探索和发现旋转后图形上的每一点都绕着旋转中心转动了相同的角度，但图形的形状和大小都没有变化；‎ 本节课数学知识技能虽相对简单，但数学思想方法与旋转变换的内涵十分丰富，应该重视数学方法的渗透。‎ 教学重点与难点：‎ 教学重点：旋转的有关概念及性质。‎ 教学难点：概念的形成过程与性质的探究过 ‎ 教学之前用《图形的旋转》的相关教学材料，找了很多教案和材料作参考，了解教学的重点和难点，确定课堂教学方法和流程。然后根据课堂教学需要，用上搜索下载《图形的旋转 》的文字资料和图片资料，做成PPT课件通过多媒体进行课堂演示，便于学生直观形象感受图形的旋转，理解图形旋转变换中蕴含的数学思想。‎ 一、 教学方法 本节课采用“问题情境——建立模型——解释、应用与拓展”的模式展开，引导学生自己提出问题、解决问题、拓展问题，指导学生用观察、抽象、自主探究为主、合作交流为辅的方法进行学习。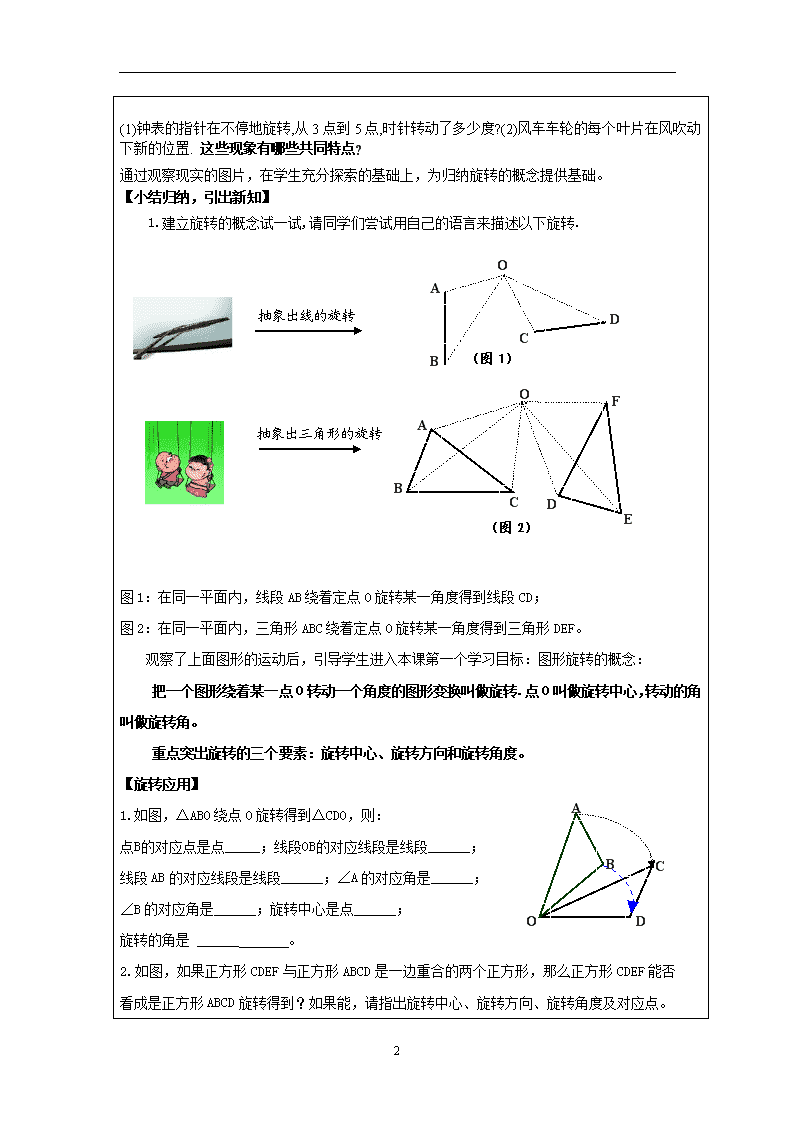‎ 一、 教学过程 ‎【创设情景，激发兴趣】‎ 列举日常生活中的实例：感受旋转 ‎ ‎ ‎ ‎ 4‎ ‎ ‎ ‎(1)钟表的指针在不停地旋转,从3点到5点,时针转动了多少度?(2)风车车轮的每个叶片在风吹动下新的位置. 这些现象有哪些共同特点?‎ 通过观察现实的图片，在学生充分探索的基础上，为归纳旋转的概念提供基础。‎ ‎【小结归纳，引出新知】‎ ‎1.建立旋转的概念试一试,请同学们尝试用自己的语言来描述以下旋转.‎ 抽象出线的旋转 ‎·‎ O A B C D ‎（图1）‎ 抽象出三角形的旋转 ‎·‎ O A B C F D E ‎（图2）‎ 图1：在同一平面内，线段AB绕着定点O旋转某一角度得到线段CD；‎ 图2：在同一平面内，三角形ABC绕着定点O旋转某一角度得到三角形DEF。‎ 观察了上面图形的运动后，引导学生进入本课第一个学习目标：图形旋转的概念：‎ 把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.点O叫做旋转中心，转动的角叫做旋转角。‎ 重点突出旋转的三个要素：旋转中心、旋转方向和旋转角度。‎ C A B O D ‎【旋转应用】‎ ‎1.如图，△ABO绕点O旋转得到△CDO，则：‎ 点B的对应点是点_____；线段OB的对应线段是线段______；‎ 线段AB的对应线段是线段______；∠A的对应角是______；‎ ‎∠B的对应角是______；旋转中心是点______；‎ 旋转的角是 ______ 。‎ ‎2.如图，如果正方形CDEF与正方形ABCD是一边重合的两个正方形，那么正方形CDEF能否 看成是正方形ABCD旋转得到？如果能，请指出旋转中心、旋转方向、旋转角度及对应点。‎ 4‎ ‎ ‎ D C A B E F ‎3.如图，香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中的一瓣经过几次旋转得到的? 旋转角∠AOB多少度？你知道∠COD等于多少度吗？ ‎ ‎·‎ ‎·‎ A B O D C ‎【实践操作，再探新知】‎ 做一做：‎ 如图，在硬纸板上，挖出一个三角形ABC，再挖一个小洞O作为旋转中心，硬纸板下面放 一张白纸。先在纸上描出这个挖掉的三角形图案 ‎·‎ O A B C F D E ‎（△ABC），然后围绕旋转中心转动硬纸板，再 描出这个挖掉的三角形（△DEF），移开硬 纸板。‎ 问题：请指出旋转中心和各对应点，哪一个角 是旋转角？‎ ‎1．从我们看到的旋转现象以及你所完成的实验中，你认为旋转主要因素是什么？‎ ‎2．在图形的旋转过程中，哪些发生了改变？哪些没有发生改变？‎ ‎ 图形的位置 图形的形状和大小 ‎ 量一量线段OA与线段OD的关系怎样（这里包括数量关系和位置关系），线段OB和OE，OC和OF呢？AB与DE呢？‎ ‎3．你能通过度量角的方法得出旋转角度吗？你准备度量哪个角？‎ 教师提供给学生动态的旋转图形，进行指导并参与讨论交流，而后归纳出旋转的特征。‎ 1． 旋转前后的图形全等；‎ 2． 对应点到旋转中心的距离相等；‎ 3． 对应点与旋转中心连线段的夹角等于旋转角。‎ 4‎ ‎ ‎ ‎【巩固新知，形成技能】‎ ‎1．如图，如果把钟表的指针看做四边形AOBC，它绕O点旋转得到四边形DOEF.在这个旋转过程中： ‎ ‎（1）旋转中心是什么? ‎ ‎（2）经过旋转，点A、B分别移动到什么位置？‎ ‎（3）旋转角是什么？‎ ‎（4）AO与DO的长有什么关系？BO与EO呢？‎ ‎（5）∠AOD与∠BOE有什么大小关系？‎ O A B D E C F C A B D E M ‎2．如图,正方形ABCD中，E是AD上一点，将△CDE逆时针旋转后得到△CBM.如连结EM,那么△CEM是怎样的三角形?‎ ‎【回顾反思，深化提高】‎ 学生小结：自主小结和交流知识学习的收获，过程经历的感受，数学思想的感悟，学习方法的体会等，或提出疑问进行讨论；‎ 教师小结：帮助学生整理所学知识，引导学生进一步体会探究学习的过程和方法，领会数学的思想。‎ 教学反思 课堂教学是一个动态过程，学生的思维又常常受到课堂气氛或突发事件的影响，为了达到最佳的教学效果，我一方面采取多媒体辅助教学，旨在呈现更直观的形象，提高学生的积极性和主动性，并提高课堂效率。另一方面采取“问题情境——建立模型——解释、应用与拓展”的学习模式展开，引导学生自己提出问题、解决问题、拓展问题，指导学生用观察、抽象、自主探究为主、合作交流为辅的方法进行学习。‎ 4‎