北师版七年级数学下册-期末检测题 7页

期末检测题 (时间：120 分钟满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．下列图形中，是轴对称图形的是(A) 2．下列运算正确的是(C) A．a2＋a3＝a5B．(a－2)2＝a2－4 C．2a2－3a2＝－a2D．(a＋1)(a－1)＝a2－2 3．某红外线遥控器发出的红外线波长为 0.00000094m，用科学记数法表示这个数据是(A) A．9.4×10－7mB．9.4×107m C．9.4×10－8mD．0.94×10－6m 4．甲、乙、丙、丁四个同学在判断时钟的时针与分针在某一时刻是否互相垂直时，下列 说法正确的是(C) A．甲说 3 点 30 分 B．乙说 12 点 15 分 C．丙说 3 点 D．丁说 6 点 15 分 5．甲、乙、丙 3 人聚会，每人带了一件从外盒包装上看完全相同的礼物(里面的东西只 有颜色不同)，将 3 件礼物放在一起，每人从中随机抽取一件．下列事件是必然事件的是(A) A．乙抽到一件礼物 B．乙恰好抽到自己带来的礼物 C．乙没有抽到自己带来的礼物 D．只有乙抽到自己带来的礼物 6．如图，直线 EF 分别与直线 AB，CD 相交于点 G，H，已知∠1＝∠2＝50°，GM 平 分∠HGB 交直线 CD 于点 M.则∠3 等于(B) A．60°B．65°C．70°D．130° ,第 6 题图) ,第 7 题图) ,第 8 题图) 7．一副分别含有 30°和 45°角的两个直角三角板，拼成如图所示的图形，其中∠C＝ 90°，∠B＝45°，∠E＝30°，则∠BFD 的度数是(A) A．15°B．25°C．30°D．10° 8．如图，点 A 在 DE 上，AC＝EC，∠1＝∠2＝∠3，则 DE 等于(B) A．BCB．ABC．DCD．AE＋AC 9．如图，把一个小球垂直向上抛出，则下列描述该小球的运动速度 v(单位：m/s)与运动 时间 t(单位：s)关系的图象中，正确的是(C) 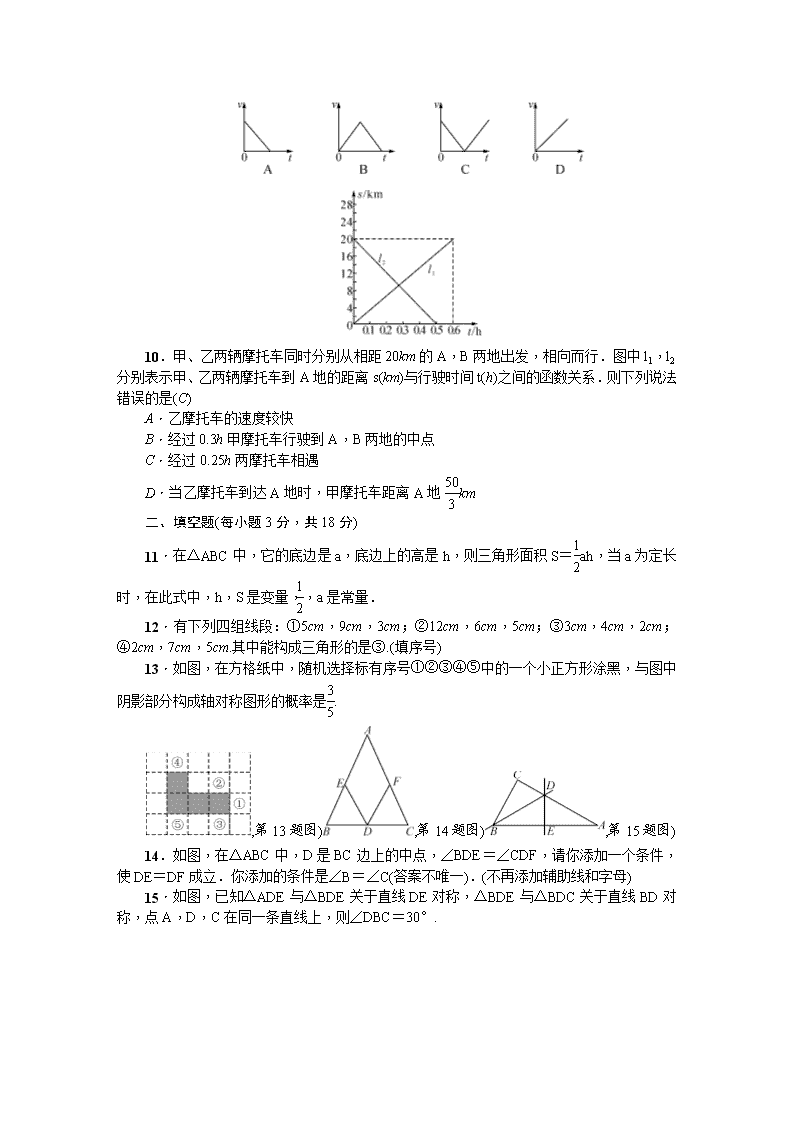10．甲、乙两辆摩托车同时分别从相距 20km 的 A，B 两地出发，相向而行．图中 l1，l2 分别表示甲、乙两辆摩托车到 A 地的距离 s(km)与行驶时间 t(h)之间的函数关系．则下列说法 错误的是(C) A．乙摩托车的速度较快 B．经过 0.3h 甲摩托车行驶到 A，B 两地的中点 C．经过 0.25h 两摩托车相遇 D．当乙摩托车到达 A 地时，甲摩托车距离 A 地 50 3 km 二、填空题(每小题 3 分，共 18 分) 11．在△ABC 中，它的底边是 a，底边上的高是 h，则三角形面积 S＝1 2ah，当 a 为定长 时，在此式中，h，S 是变量，1 2 ，a 是常量． 12．有下列四组线段：①5cm，9cm，3cm；②12cm，6cm，5cm；③3cm，4cm，2cm； ④2cm，7cm，5cm.其中能构成三角形的是③.(填序号) 13．如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中 阴影部分构成轴对称图形的概率是3 5. ,第 13 题图) ,第 14 题图) ,第 15 题图) 14．如图，在△ABC 中，D 是 BC 边上的中点，∠BDE＝∠CDF，请你添加一个条件， 使 DE＝DF 成立．你添加的条件是∠B＝∠C(答案不唯一)．(不再添加辅助线和字母) 15．如图，已知△ADE 与△BDE 关于直线 DE 对称，△BDE 与△BDC 关于直线 BD 对 称，点 A，D，C 在同一条直线上，则∠DBC＝30°. 16．如图，一架梯子 AB 斜靠在与地面 OM 垂直的墙壁 ON 上，梯顶 A 与地面的垂直距 离为 4 米，梯脚 B 与墙角 O 的水平距离为 3 米，若梯子顶端 A 沿 NO 下滑，同时底端 B 沿 OM 向右滑行．设点 A 下滑到点 C，点 B 向右滑行到点 D，并且∠ODC＝∠OAB，则梯子顶 端 A 沿 NO 下滑的距离为 1 米． 三、解答题(共 72 分) 17．(6 分)2－2－(π－3.14)0＋(－0.5)2020×22020. 解：原式＝1 4 －1＋(－0.5×2)2020＝1 4 －1＋1＝1 4 18．(6 分)已知一个纸箱中放有大小相同的 10 个白球和若干个黄球．从箱中随机地取出 一个是白球的概率是2 5 ，再往箱中放进 20 个白球，求随机地取出一个黄球的概率． 解：设黄球有 x 个，根据题意得， 10 10＋x ＝2 5 ，解得 x＝15，则再往箱中放进 20 个白球， 随机地取出一个黄球的概率为 15 10＋15＋20 ＝1 3 19．(6 分)先化简，再求值：(y＋2)(y2－2y＋1)－y(y2＋1)，其中 y＝1 2. 解：(y＋2)(y2－2y＋1)－y(y2＋1)＝y3－2y2＋y＋2y2－4y＋2－y3－y＝－4y＋2，当 y＝1 2 时，原式＝－2＋2＝0 20．(6 分)如图，直线 AB∥CD，EF⊥CD，F 为垂足，∠GEF＝30°，求∠1 的度数． 解：∵EF⊥CD 于点 F，∴∠EFG＝90°，∴∠EGF＝90°－∠GEF＝90°－30°＝60 °，∵∠CGE＋∠EGF＝180°， ∴∠CGE＝180°－60°＝120°， ∵AB∥CD， ∴∠1＝∠CGE＝120°(两直线平行，同位角相等) 21．(8 分)如图，将 Rt△ABC 沿某条直线折叠，使斜边的两个端点 A 与 B 重合，折痕为 DE. (1)如果 AC＝6cm，BC＝8cm，试求△ACD 的周长； (2)如果∠CAD∶∠BAD＝1∶2，求∠B 的度数． 解：(1)由折叠的性质可知，DE 垂直平分线段 AB，根据垂直平分线的性质可得 DA＝DB， ∴DA＋DC＋AC＝DB＋DC＋AC＝BC＋AC＝14cm (2)设∠CAD＝x，则∠BAD＝2x，∵DA＝DB，∴∠B＝∠BAD＝2x，在 Rt△ABC 中， ∠B＋∠BAC＝90°，即 2x＋2x＋x＝90°，解得 x＝18°，∴∠B＝2x＝36° 22．(8 分)如图，在△ABC 中，∠ACB＝90°，AC＝BC，AE 是 BC 边上的中线，过 C 作 CF⊥AE，垂足为 F，过 B 作 BD⊥BC 交 CF 的延长线于 D. (1)试说明 AE＝CD； (2)若 AC＝12cm，求 BD 的长． 解：(1)由△ACE≌△CBD 可得 AE＝CD (2)由(1)得 BD＝EC，由 EC＝1 2BC＝1 2AC 可得 BD＝6cm 23．(10 分)如图，AB∥CD，以点 A 为圆心，小于 AC 长为半径作圆弧，分别交 AB， AC 于 E，F 两点，再分别以 E，F 为圆心，大于 1 2EF 长为半径作圆弧，两条圆弧交于点 P， 作射线 AP，交 CD 于点 M. (1)若∠ACD＝124°，求∠MAB 的度数； (2)若 CN⊥AM，垂足为 N，试说明△CAN≌△CMN. 解：(1)∠MAB＝1 2(180°－124°)＝28° (2)∵AB∥CD，∴∠CMA＝∠MAB， ∵∠MAB＝∠CAM，∴∠CAM＝∠CMA， 又∵CN⊥AM，∴∠CNA＝∠CNM＝90°， 在△CAN 和△CMN 中， ∠CAM＝∠CMA， ∠CNA＝∠CNM＝90°， CN＝CN， ∴△CAN≌△CMN(AAS) 24．(10 分)我国很多城市水资源缺乏，为了加强居民的节水意识，某市制定了每月用水 4 吨以内(包括 4 吨)和用水 4 吨以上两种收费标准(收费标准：每吨水的价格)．某用户每月应 交水费 y(元)与用水量 x(吨)之间关系的图象如图所示． (1)说出自来水公司在这两个用水范围内的收费标准； (2)当 x>4 时，求因变量 y 与自变量 x 之间的关系式； (3)若某用户该月交水费 26 元，求他用了多少吨水？ 解：(1)4 吨以内，每吨为8 4 ＝2(元)；4 吨以上，每吨为错误!＝3(元) (2)当 x＞4 时，y＝8＋3(x－4)＝3x－4，即 y＝3x－4 (3)∵y＝26，∴3x－4＝26，解得 x＝10，则该月他用了 10 吨水 25．(12 分)已知，在△ABC 中，AC＝BC，分别过 A，B 点作互相平行的直线 AM，BN， 过点 C 的直线分别交直线 AM，BN 于点 D，E. (1)如图①，若 AM⊥AB，试说明：CD＝CE； (2)如图②，∠ABC＝∠DEB＝60°，试说明：AD＋DC＝BE. 解：(1)如图①，延长 AC 交 BN 于点 F， ∵AC＝BC，∴∠CAB＝∠CBA， 又∵AB⊥AM，∴∠BAM＝90°， 又∵AM∥BN，∴∠BAM＋∠ABN＝180°， ∴∠ABN＝90°， ∴∠BAF＋∠AFB＝90°，∠ABC＋∠CBF＝90°， ∴∠CBF＝∠AFB， ∴BC＝CF，∴AC＝FC， 又∵AM∥BN，∴∠DAF＝∠AFB， 在△ADC 和△FEC 中， ∠DAC＝∠EFC， AC＝FC， ∠ACD＝∠FCE， ∴△ADC≌△FEC(ASA)，∴DC＝EC (2)如图②，在 EB 上截取 EH＝EC，连接 CH， ∵AC＝BC，∠ABC＝60°，∴△ABC 为等边三角形， ∵∠DEB＝60°，∴△CHE 是等边三角形， ∴∠CHE＝60°，∠HCE＝60°，∴∠BHC＝120°， ∵AM∥BN，∴∠ADC＋∠BEC＝180°， ∴∠ADC＝120°，∴∠DAC＋∠DCA＝60°， 又∵∠DCA＋∠ACB＋∠BCH＋∠HCE＝180°， ∴∠DCA＋∠BCH＝60°，∴∠DAC＝∠BCH， 在△DAC 与△HCB 中， ∠DAC＝∠HCB， ∠ADC＝∠CHB， AC＝CB， ∴△DAC≌△HCB(AAS)， ∴AD＝CH，DC＝BH， 又∵CH＝CE＝HE， ∴BE＝BH＋HE＝DC＋AD