七年级下册数学教案4-4 用尺规作三角形 北师大版 2页

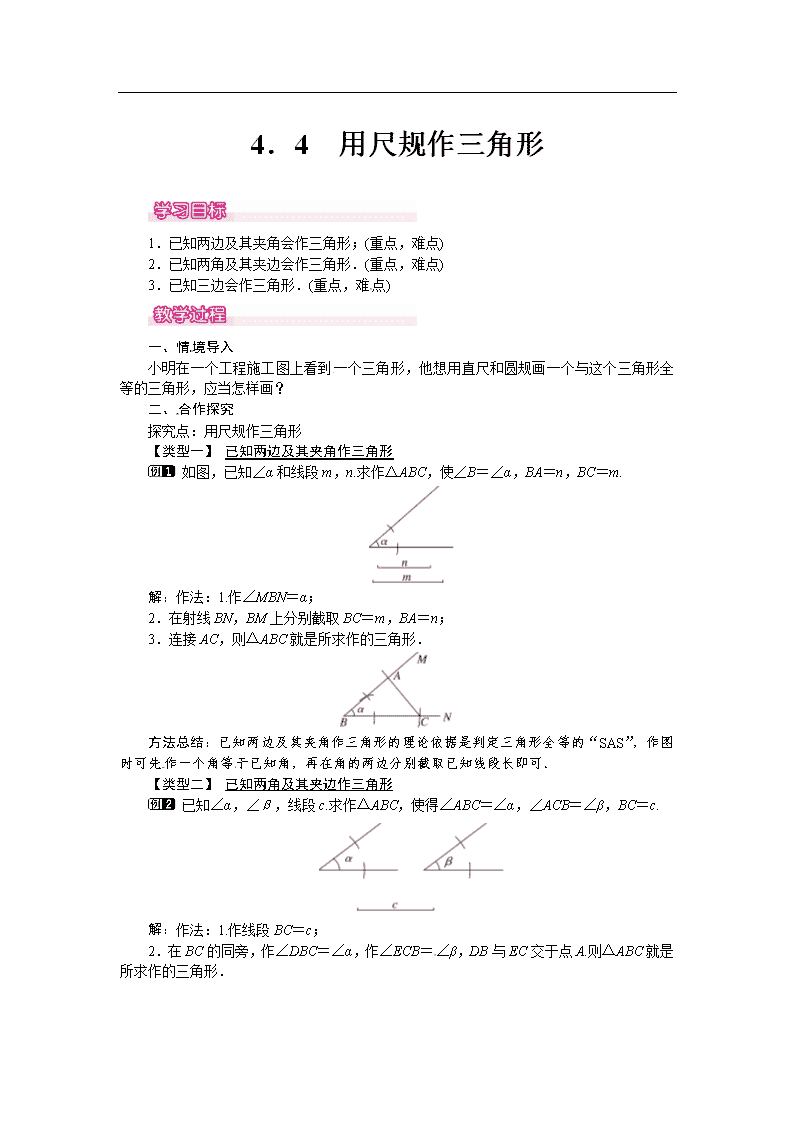
‎4．4　用尺规作三角形 ‎1．已知两边及其夹角会作三角形；(重点，难点)‎ ‎2．已知两角及其夹边会作三角形．(重点，难点)‎ ‎3．已知三边会作三角形．(重点，难点)　　　　　　　　　　　　　　‎ 一、情境导入 小明在一个工程施工图上看到一个三角形，他想用直尺和圆规画一个与这个三角形全等的三角形，应当怎样画？‎ 二、合作探究 探究点：用尺规作三角形 ‎【类型一】 已知两边及其夹角作三角形 ‎ 如图，已知∠α和线段m，n.求作△ABC，使∠B＝∠α，BA＝n，BC＝m.‎ 解：作法：1.作∠MBN＝α；‎ ‎2．在射线BN，BM上分别截取BC＝m，BA＝n；‎ ‎3．连接AC，则△ABC就是所求作的三角形．[来源:Z§xx§k.Com]‎ ‎[来源:学*科*网Z*X*X*K]‎ 方法总结：已知两边及其夹角作三角形的理论依据是判定三角形全等的“SAS”，作图时可先作一个角等于已知角，再在角的两边分别截取已知线段长即可．　　‎ ‎【类型二】 已知两角及其夹边作三角形[来源:学,科,网][来源:学#科#网]‎ ‎ 已知∠α，∠β，线段c.求作△ABC，使得∠ABC＝∠α，∠ACB＝∠β，BC＝c.‎ 解：作法：1.作线段BC＝c；‎ ‎2．在BC的同旁，作∠DBC＝∠α，作∠ECB＝∠β，DB与EC交于点A.则△ABC就是所求作的三角形．‎ 方法总结：已知两角及其夹边作三角形的理论依据是判定三角形全等的“ASA”，作图时可先作一条边等于已知边，再在这条边的同侧，以边的两个端点为顶点作两个角分别等于已知角即可．‎ ‎【类型三】 已知三边作三角形 ‎ 已知三条线段a、b、c，用尺规作出△ABC，使BC＝a，AC＝b、AB＝c.‎ 解：作法：1.作线段BC＝a；‎ ‎2．以点C为圆心，以b为半径画弧，再以B为圆心，以c为半径画弧，两弧相交于点A；‎ ‎3．连接AC和AB，则△ABC即为所求作的三角形，如图所示．[来源:Zxxk.Com]‎ 方法总结：已知三角形三边的长，根据全等三角形的判定“SSS”，知三角形的形状和大小也就确定了．作三角形相当于确定三角形三个顶点的位置．因此可先确定三角形的一条边(即两个顶点)，再分别以这条边的两个端点为圆心，以已知线段长为半径画弧，两弧的交点即为另一个顶点．‎ 三、板书设计 ‎1．已知两边及其夹角作三角形 ‎2．已知两角及其夹边作三角形 ‎3．已知三边作三角形 ‎ 本节课学习了有关三角形的作图，主要包括两种基本作图：作一条线段等于已知线段，作一个角等于已知角．作图时，鼓励学生一边作图，一边用几何语言叙述作法，培养学生的动手能力、语言表达能力