青岛初中数学七年级下册用加减法解二元一次方程 17页

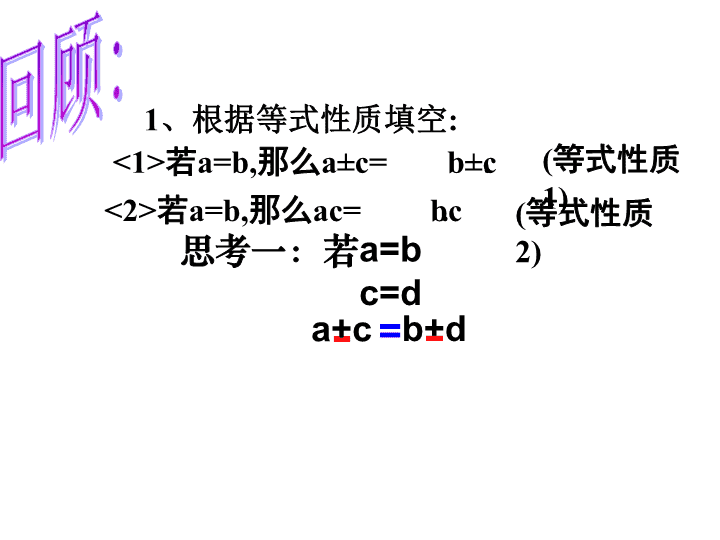
1．会用加减消元法解二元一次方程组． 2．了解解二元一次方程组的消元方法，经历从 “二元”到“一元”的转化过程，体会解二元 一次方程组中化“未知”为“已知”的“转化” 的思想方法． 目标展示 1、根据等式性质填空: b±c bc (等式性质1) (等式性质2)<2>若a=b,那么ac= . <1>若a=b,那么a±c= . b+d 思考一：若a=b c=d =- -a+c 思考二： 3a-2b=1 3a+2b=5 ① ②3a+4b=7 6a = 6 ① ②＋① ②_ -6b = -6 6b = 6 ② ①_ 2、解方二元一次程组的基本思路是什么？ 二元一次方程组 一元一次方程消元 代入法 动动脑(1）方程组中各个未知数的系数有什么特点？ （2）分组讨论看除代入法外还有没有其它的解法？ 我们已经学过了用代入法解下列 二元一次方程组，还有别的方法吗？ x+y=7300 x-y=6100 ① ② x+y=7300 x﹣y=6100｛ ② ① 解: 2x=13400 解得 x=6700 把x=6700代入①,得 6700+y=7300 解得 y=600 所以｛ x=6700 y=600 ① + ② ,得 通过把两个方程 相加或相减消去 一个未知数，从 而转化为解一元 一次方程，方程 组的这种解法叫 做加减消元法， 简称加减法。 分别相加 y 1.已知方程组 x+3y=17 2x-3y=6 两个方程左右两边 就可以消去未知数 分别相减 2.已知方程组 25x-7y=16 25x+6y=10 两个方程左右两边 就可以消去未知数 x ①+② 得：4x=4 把 x=1代入②得： 3x -2 y =-1 ① ②｛例 题 解方程组 x +2 y =5 解得 x=1 1+2y=5 解得：y=2 x=1 y=2 ｛所以 3x + y = 5 ② - ①得：3y=6 解得 y=2 把 y=2代入②得： 3x+2=5 解得：x=1 x=1 y=2 ｛所以 3y=6 在方程组的两个方程中，若某个未知数的 系数互为相反数，则可以直接 若某个未知数系数相等，则可以直接将方程 中 的两边分别 消去这个未知数 把这两个方程的两边分别相加 相减 消去这个未知数 用加减法解下列方程组 2x-y=-4 3x+y=19 1、 2x+y=-7 2x-3y=5 2、 3u-5v=2 3u+2v=9 3、A层 B层 C层 解方程组 5u 10u+4v =-18 ① 3u - 4v = -8 ② +2v = -9 ① ①x2 3u - 4v = -8 ② 6x+21y=27 ① 6x+10y=16 ② 2x+7y=9 ① 3x+5y=8 ② ①x3 ②x2 3 5 8 7 5 2 x y x y      2 3 1 3 5 4 y x x y       2 3 5 3 7 x y x y      ① ② ① ② 1.（ ）用加减消元法解方程组 ，将两个方程相加得（ ） A．3x=8 B．7x=2 C．10x=8 D．10x=10 2.（ ）用加减消元法解方程组 ，①－②得（ ） A．2y=1 B．5y=4 C．7y=5 D．－3y=-3 3.（ ）用加减消元法解方程组 正确的方法是（ ） A．①+②得2x=5 B．①+②得3x=12 C．①+②得3x+7=5 D．先将②变为x－3y=7③，再①－③得x=-2 D C D 5 1 1 2 m x n x m y n y          的 解 是      532 425 yx yx 4.（ ）已知方程组 , 则m= ，n= ． 5.（ ）用加减消元法解方程组 2 3 x=2 y=3 同学们：你从上面的学习中能体会到用 加减法解方程组主要步骤有哪些吗？ 你会用加减法解方程组了么？ 二元一次方程组 一元一次方程代入消元法 加减消元法 作业： A层：必做 P55页 习题 2、(1) (2) 选做：3、（1） B层：必做 P55页 习题 2、(1) (2) 选做：P55练习1、（4） C层：必做 P55页 习题 2、(1) (2) 解方程组      22)(3)1(5 132 yxx yx 教师寄语： 假如生活是一条河流，愿你 是一叶执著向前的小舟；假 如生活是一叶小舟，愿你是 个风雨无阻的水手。