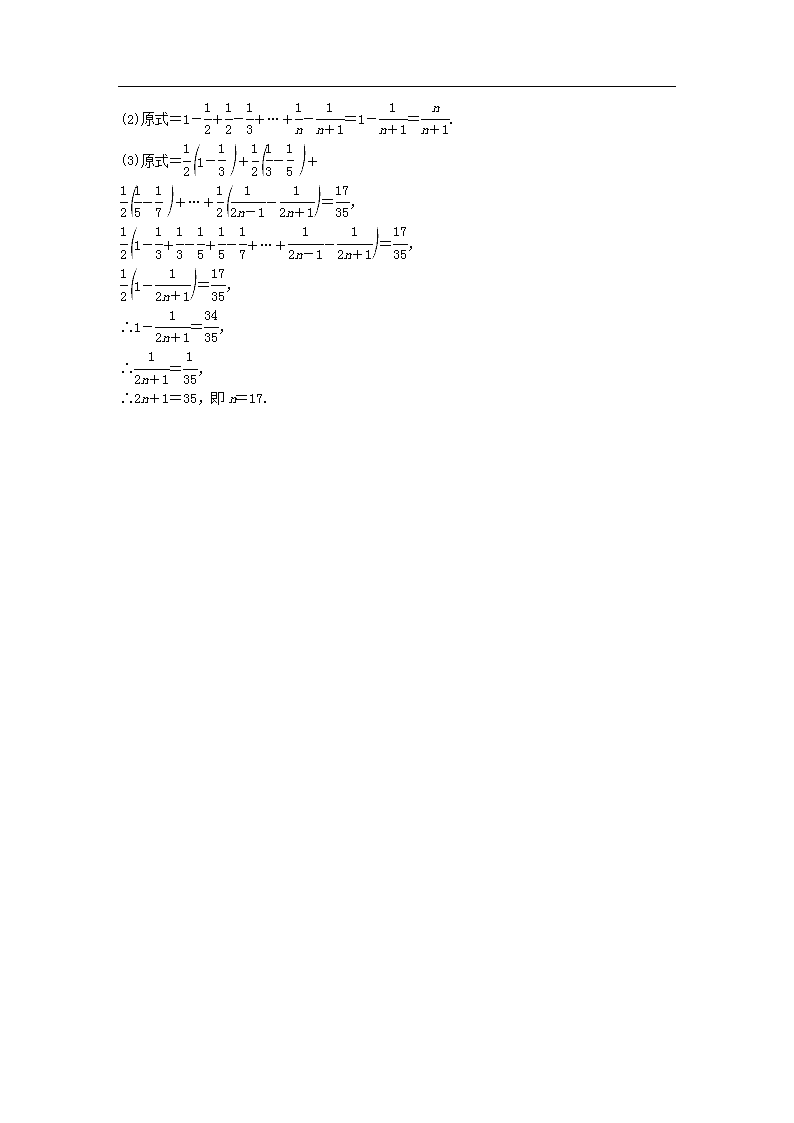浙教版数学七年级上册《用字母表示数》练习题 3页

4．1 用字母表示数 1．用字母表示数，下列书写规范的是(DＸ) ＴA.Ｘa2 ＴB.Ｘ－1x ＴC.Ｘ11 2 a ＴD.Ｘ2a2 2．甲数比乙数的 2 倍大 3，若乙数为 x，则甲数为(BＸ) ＴA.Ｘ2x－3 ＴB.Ｘ2x＋3 ＴC.Ｘ1 2 x－3 ＴD.Ｘ1 2 x＋3 3．已知长方体的长、宽、高分别为 a，b，c，则其表面积 S 的计算公式为(CＸ) ＴA.ＸS＝ab＋bc＋ca ＴB.ＸS＝abc ＴC.ＸS＝2(ab＋bc＋ac) ＴD.ＸS＝6ab 4．小明买了 n(ＴkgＸ)橘子，花了 m 元，则这种橘子的单价是(BＸ) ＴA.Ｘn m 元/Ｔ千克Ｘ ＴB.Ｘm n 元/Ｔ千克Ｘ ＴC.Ｘmn 元/Ｔ千克Ｘ ＴD.Ｘ(m－n)元/Ｔ千克Ｘ 5．一个高为 20 的圆柱的体积是 20S，其中 S 表示(BＸ) ＴA.Ｘ该圆柱的底面半径 ＴB.Ｘ该圆柱一个底面的面积 ＴC.Ｘ该圆柱两个底面的面积之和 ＴD.Ｘ该圆柱的底面直径 6．如果用 m 表示任意实数，那么： (1)m 的相反数可表示为__－m__； (2)m 的绝对值可表示为__|m|__； (3)m 的 2 1 2 倍可表示为__5 2 m__； (4)比 m 大 5 的数可表示为__m＋5__； (5)m 的平方与 8 的差可表示为__m2－8__． 7．三个连续自然数，如果中间的数为 n，那么其余两个数分别是 n－1，n＋1． 8．已知一本书的价格为 x 元，则 0.9x 可解释为该书打九折出售的价格(答案不唯一)． 9．体育委员带了 500 元钱去买体育用品．已知一个足球 a 元，一个篮球 b 元，一个排球 c 元．请说出下列各式所表示的含义： (1)a＋b；(2)500－3b；(3)2(a＋b＋c)． 【解】 (1)买一个足球和一个篮球所需的钱． (2)买三个篮球后剩下的钱． (3)买两个足球、两个篮球、两个排球所需的钱． 10．如图，用字母表示图中阴影部分的面积． (第 10 题) 【解】 1 2 (b－a)h. 11．已知正方体的棱长为 a，当其棱长增加 x 时，体积增加了(CＸ) ＴA.Ｘa3－x3 ＴB.Ｘx3 ＴC.Ｘ(a＋x)3－a3 ＴD.Ｘ(a＋x)3－x3 12．若用 100 元可购买 n 本书，且每本书需另加邮寄费 6 分，则购买 n 本书共需(DＸ) ＴA.Ｘ(100＋0.6)n 元 ＴB.Ｘ(100.06＋n)元 ＴC.Ｘ(0.06＋100n)元 ＴD.Ｘ(100＋0.06n)元 13．若 n 表示一个三位数，现把 2 放在它的右边，得到一个四位数，则这个四位数可表示为 __10n＋2__；若把 2 放在它的左边，则这个新的四位数可表示为__2000＋n__． 【解】 把 2 放在三位数 n 的右边时，2 在个位上，原三位数 n 就扩大了 10 倍，所以是 10n ＋2；把 2 放在三位数 n 的左边时，2 在千位上，所以是 2000＋n. 14．如图是一座楼梯的侧面示意图，如果要在楼梯上铺一条地毯，那么这条地毯至少要多少 长？若楼梯的宽为 b，则地毯的面积为多少？ (第 14 题) 【解】 地毯的长为(a＋h)ＴmＸ. 当楼梯的宽为 b 时，地毯的面积为(a＋h)b＝(ab＋hb)(ＴmＸ2)． 15．先观察下列等式，然后用你发现的规律解答后面的问题： 1 1×2 ＝1－1 2 ， 1 2×3 ＝1 2 －1 3 ， 1 3×4 ＝1 3 －1 4 ，…. (1)计算： 1 1×2 ＋ 1 2×3 ＋ 1 3×4 ＋…＋ 1 9×10 ； (2)探究： 1 1×2 ＋ 1 2×3 ＋ 1 3×4 ＋…＋ 1 n（n＋1） ＝__________(用含 n 的式子表示)； (3)若 1 1×3 ＋ 1 3×5 ＋ 1 5×7 ＋…＋ 1 （2n－1）（2n＋1） ＝17 35 ，求 n 的值． 【解】 (1)原式＝1－1 2 ＋1 2 －1 3 ＋…＋1 9 － 1 10 ＝1－ 1 10 ＝ 9 10 . (2)原式＝1－1 2 ＋1 2 －1 3 ＋…＋1 n － 1 n＋1 ＝1－ 1 n＋1 ＝ n n＋1 . (3)原式＝1 2 1－1 3 ＋1 2 1 3 －1 5 ＋ 1 2 1 5 －1 7 ＋…＋1 2 1 2n－1 － 1 2n＋1 ＝17 35 ， 1 2 1－1 3 ＋1 3 －1 5 ＋1 5 －1 7 ＋…＋ 1 2n－1 － 1 2n＋1 ＝17 35 ， 1 2 1－ 1 2n＋1 ＝17 35 ， ∴1－ 1 2n＋1 ＝34 35 ， ∴ 1 2n＋1 ＝ 1 35 ， ∴2n＋1＝35，即 n＝17.