多边形的内角和与外角和教案2 4页

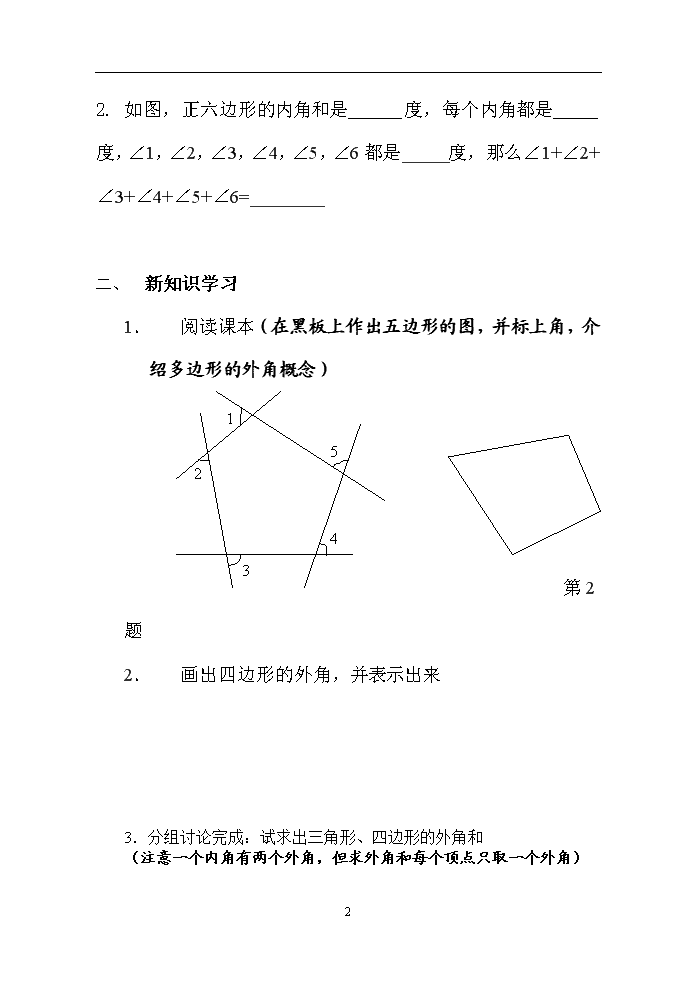
‎ ‎ ‎ 多边形的内角和与外角和 ‎【教学目标】：‎ 1． 了解多边形外角定义，并能准确找出多边形的外角；‎ 2． 掌握多边形的外角和公式，利用内角和与外角和公式解决实际问题；通过对内角、外角之间的关系，体会知识之间的内在联系。‎ 3． 经历多边形外角和的探索过程，培养学生主动探索习惯。‎ ‎【教学重难点】：‎ 重点：理解多边形外角含义，多边形外角和公式 难点：多边形外角和公式的探索过程；利用多边形内角和、外角和公式解决实际问题。‎ ‎【教学过程】：‎ 一、 课前练习（通过课前练习，让学生复习上节课所学知识，回忆本节课涉及到的旧知识）‎ ‎1‎ ‎3‎ ‎2‎ ‎4‎ ‎6‎ ‎5‎ ‎1.五边形的内角和是________________‎ 4‎ ‎ ‎ ‎2. 如图，正六边形的内角和是______度，每个内角都是_____度，∠1，∠2，∠3，∠4，∠5，∠6都是_____度，那么∠1+∠2+∠3+∠4+∠5+∠6=________‎ 一、 新知识学习 1． 阅读课本（在黑板上作出五边形的图，并标上角，介绍多边形的外角概念）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎ 第2题 2． 画出四边形的外角，并表示出来 ‎3．分组讨论完成：试求出三角形、四边形的外角和 ‎（注意一个内角有两个外角，但求外角和每个顶点只取一个外角）‎ 4‎ ‎ ‎ ‎（要求学生在练习本上画出图形，找出外角，动手操作完成。先由较简单的三角形、四边形入手）‎ ‎4．你是怎样得到的？你能想出多少种方法？‎ ‎（让学生介绍方法）‎ ‎（①以小明自身转过的度数计算；②用量角器量出度数后计算；③把各个外角都剪出来，再拼在一起，类似验证三角形内角和的方法；④课本P111方法⑤利用内角和结论推理得出）‎ ‎5．那么五边形、六边形的外角和还会有类似的结论吗？动手试一试。‎ ‎（分组运用之前介绍的方法完成）‎ ‎6．通过多次计算，归纳得出多边形外角和结论 ‎7．“议一议”‎ ‎（1）你能运用多边形内角和结论推导出多边形外角和结论吗？‎ 提示：一个外角和内角和是180°，可以用含有多边形的内角的代数式表示多边形的外角，再得出多边形的外角和，最后得出多边形的外角和结论。‎ 外角=180°-内角 外角和=（180°—内角）·n ‎ =180°·n—外角·n ‎ =180°n—[（n-2）·180°]=360°‎ ‎(板书，从理论上让学生感受多边形外角和公式的成立)‎ 4‎ ‎ ‎ ‎ ‎ ‎（2）反过来，你能运用多边形外角和结论推导出多边形内角和结论吗？‎ 内角=180°-外角 内角和=（180°—外角）·n ‎ =180°·n—外角·n ‎ =180°n-360°‎ ‎ =180°n-180°×2‎ ‎ =（n-2）·180°‎ ‎（充分利用内外角的关系，运用内角和、外角和结论计算，为下面完成例题打下基础）‎ 8． 例题学习：一个多边形的内角和等于它的外角和的3倍，它是几边形？‎ 三、小结：‎ ‎1．多边形一个内角有多少个外角？‎ ‎2．多边形的外角和是多少？‎ ‎3．验证多边形外角和结论有多少种方法？‎ 四、布置作业 ‎ 4‎