北师大版数学七年级下册第三章《变量之间的关系》单元检测2 8页

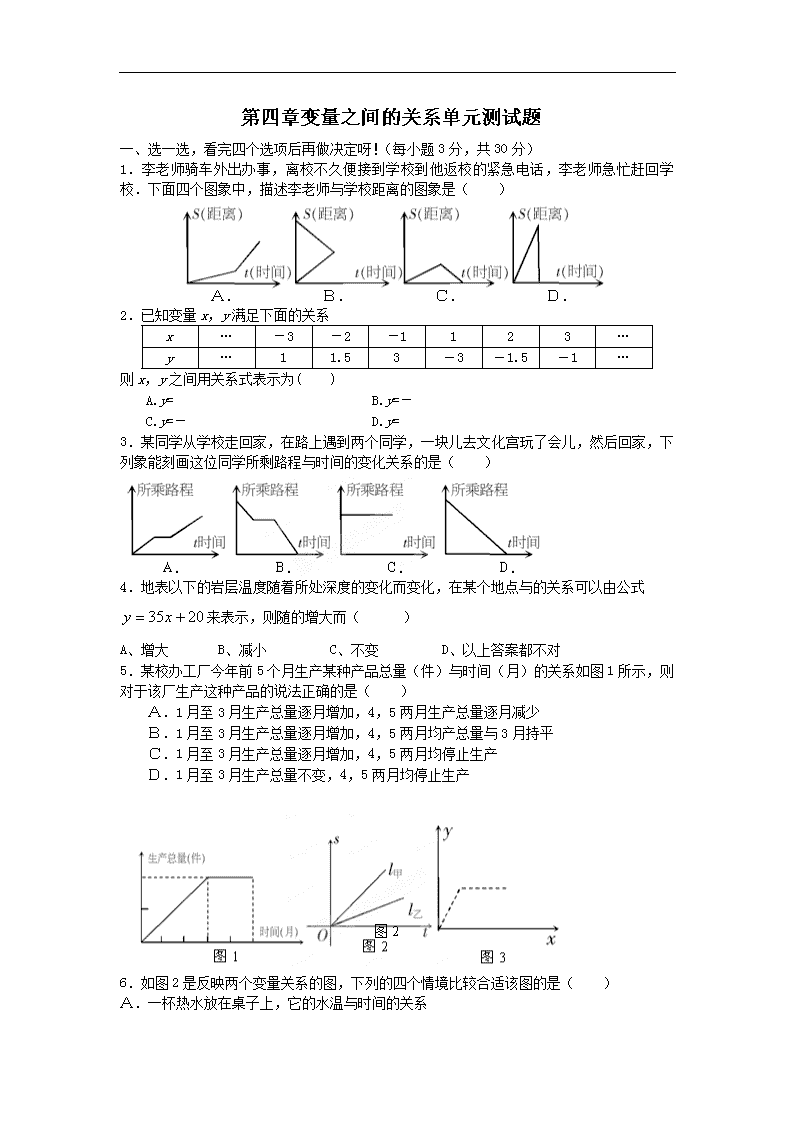
第四章变量之间的关系单元测试题 一、选一选，看完四个选项后再做决定呀！（每小题 3 分，共 30 分） 1．李老师骑车外出办事，离校不久便接到学校到他返校的紧急电话，李老师急忙赶回学校．下 面四个图象中，描述李老师与学校距离的图象是（ ） 2．已知变量 x，y 满足下面的关系 x … －3 －2 －1 1 2 3 … y … 1 1.5 3 －3 －1.5 －1 … 则 x，y 之间用关系式表示为( ) A.y= B.y=－ C.y=－ D.y= 3．某同学从学校走回家，在路上遇到两个同学，一块儿去文化宫玩了会儿，然后回家，下 列象能刻画这位同学所剩路程与时间的变化关系的是（ ） 4．地表以下的岩层温度随着所处深度的变化而变化，在某个地点与的关系可以由公式 2035  xy 来表示，则随的增大而（ ） A、增大 B、减小 C、不变 D、以上答案都不对 5．某校办工厂今年前 5 个月生产某种产品总量（件）与时间（月）的关系如图 1 所示，则 对于该厂生产这种产品的说法正确的是（ ） Ａ．1 月至 3 月生产总量逐月增加，4，5 两月生产总量逐月减少 Ｂ．1 月至 3 月生产总量逐月增加，4，5 两月均产总量与 3 月持平 Ｃ．1 月至 3 月生产总量逐月增加，4，5 两月均停止生产 Ｄ．1 月至 3 月生产总量不变，4，5 两月均停止生产 6．如图 2 是反映两个变量关系的图，下列的四个情境比较合适该图的是（ ） Ａ．一杯热水放在桌子上，它的水温与时间的关系 Ａ． Ｂ． Ｃ． Ｄ． 图 2 Ｂ．一辆汽车从起动到匀速行驶，速度与时间的关系 Ｃ．一架飞机从起飞到降落的速度与时晨的关系 Ｄ．踢出的足球的速度与时间的关系 7．如图 3，射线，分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的关系，则 图中显示的他们行进的速度关系是（ ） Ａ．甲比乙快 Ｂ．乙比甲快 Ｃ．甲、乙同速 Ｄ．不一定 8．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这 个问题中因变量是（ ） A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器 9．长方形的周长为 24 厘米，其中一边为（其中 0x ），面积为平方厘米，则这样的长方 形中与的关系可以写为（ ） A、 2xy  B、  212 xy  C、   xxy  12 D、  xy  122 10 如果没盒圆珠笔有 12 支，售价 18 元，用 y（元）表示圆珠笔的售价，x 表示圆珠笔的支 数，那么 y 与 x 之间的关系应该是（ ） （A）y=12x（B）y=18x（C）y=x（D）y=x 二、填一填，要相信自己的能力！（每小题 3 分，共 30 分） 1．某种储蓄的月利率是 0.2% ，存入100 元本金后，则本息和（元）与所存月数之间的关 系式为____（不考虑利息税）． 2．如果一个三角形的底边固定，高发生变化时，面积也随之发生改变．现已知底边长为10， 则高从变化到10时，三角形的面积变化范围是____． 3．汽车开始行驶时，油箱中有油 40 升，如果每小时耗油升，则油箱内余油量（升）与行驶 时间（小时）的关系式为____，该汽车最多可行驶____小时． 4．某公司销售部门发现，该公司的销售收入随销售量的变化而变化，其中 是自变 量， 是因变量。 5．地面温度为 15 ºC，如果高度每升高 1 千米，气温下降 6 ºC，则高度 h(千米)与气温 t(ºC)之间的关系式为 。 6．汽车以 60 千米/时速度匀速行驶，随着时间 t（时）的变化，汽车的行驶路程 s 也随着 变化，则它们之间的关系式为 。 7．小明和小强进行百米赛跑，小明比小强跑得快，如果 两人同时起跑，小明肯定赢，如图 4 所示，现在小明让小强 先跑 米，直线 表示小明的路程与时间的 关系，大约 秒时，小明追上了小强，小强在这次赛 跑中的速度是 。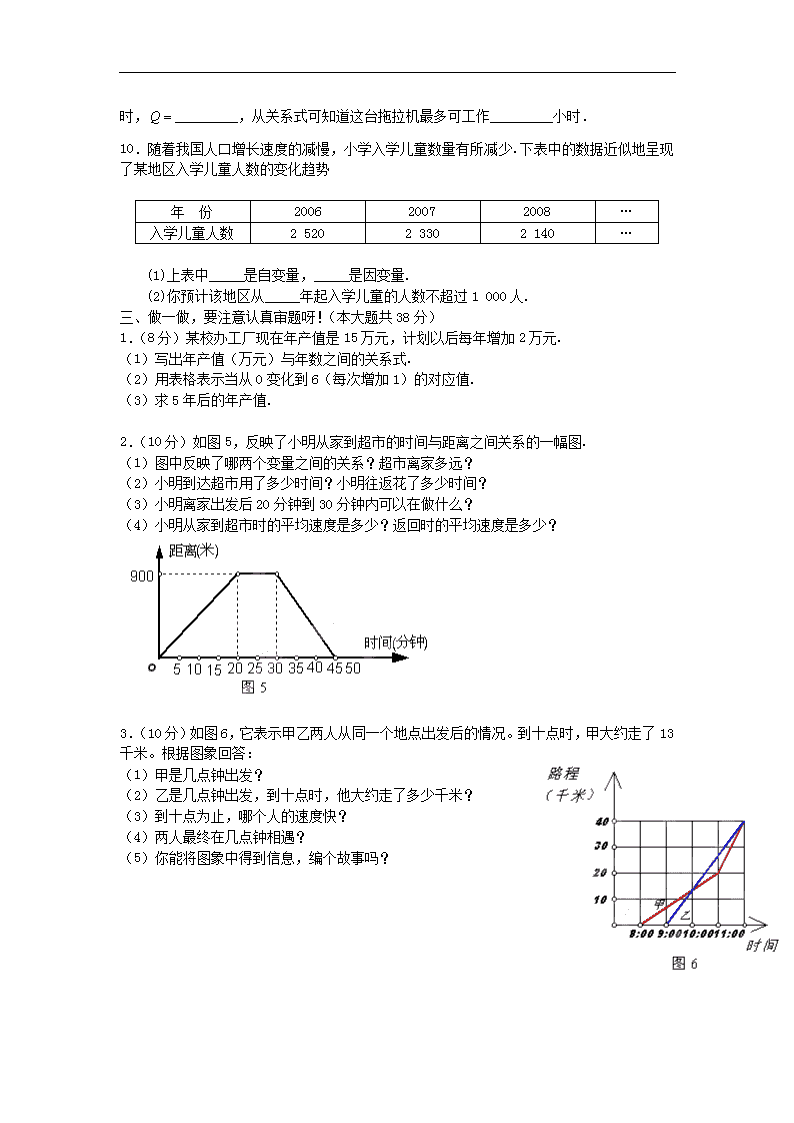 8．小雨拿 5 元钱去邮局买面值为 80 分的邮票，小雨买邮票 后所剩钱数 y（元）与买邮票的枚数 x（枚）之间的关系式 为 9．拖拉机工作时，油箱中的余油量（升）与工作时间（时）的关系式为 40 6Q t  ．当 4t  时， Q  _________，从关系式可知道这台拖拉机最多可工作_________小时． 50 80 t(秒) s(米) l2 l1 0 10 20 30 40 60 70 5 20 图 4 10．随着我国人口增长速度的减慢，小学入学儿童数量有所减少.下表中的数据近似地呈现 了某地区入学儿童人数的变化趋势 年 份 2006 2007 2008 … 入学儿童人数 2 520 2 330 2 140 … (1)上表中_____是自变量，_____是因变量. (2)你预计该地区从_____年起入学儿童的人数不超过 1 000 人. 三、做一做，要注意认真审题呀！（本大题共 38 分） 1．（8 分）某校办工厂现在年产值是 15 万元，计划以后每年增加 2 万元. （1）写出年产值（万元）与年数之间的关系式. （2）用表格表示当从 0 变化到 6（每次增加 1）的对应值. （3）求 5 年后的年产值. 2．（10 分）如图 5，反映了小明从家到超市的时间与距离之间关系的一幅图. （1）图中反映了哪两个变量之间的关系？超市离家多远？ （2）小明到达超市用了多少时间？小明往返花了多少时间？ （3）小明离家出发后 20 分钟到 30 分钟内可以在做什么？ （4）小明从家到超市时的平均速度是多少？返回时的平均速度是多少？ 3．（10 分）如图 6，它表示甲乙两人从同一个地点出发后的情况。到十点时，甲大约走了 13 千米。根据图象回答： （1）甲是几点钟出发？ （2）乙是几点钟出发，到十点时，他大约走了多少千米？ （3）到十点为止，哪个人的速度快？ （4）两人最终在几点钟相遇？ （5）你能将图象中得到信息，编个故事吗？ 4．（10 分）在一次实验中，小明把一根弹簧的上端固定．在其下端悬挂物体，下面是测得 的弹簧的长度与所挂物体质量的一组对应值． 所挂质量 / kgx 0 1 2 3 4 5 弹簧长度 / cmy 18 20 22 24 26 28 （1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ （2）当所挂物体重量为 3 千克时，弹簧多长？不挂重物时呢？ （3）若所挂重物为 7 千克时（在允许范围内），你能说出此时的弹簧长度吗？ 四、拓广探索！（本大题共 22 分） 1．（１０分）小明在暑期社会实距活动中，以每千克 0.8 元的价格从批发市场购进若干千克 瓜到市场上去销售，在销售了 40 千克西瓜之后，余下的每千克降价 0.4 元，全部售完．销 售金额与售出西瓜的千克数之间的关系如图 7 所示．请你根据图象提供的信息完成以下问 题： （1）求降价前销售金额（元）与售出西瓜（千克）之间的关系式； （2）小明从批发市场共购进多少千克西瓜？ （3）小明这次卖瓜赚子多少钱？ ２．（12 分某移动通信公司开设了两种通信业务，“全球通”：使用时首先缴 50 元月租费， 然后每通话 1 分钟，自付话费 0.4 元；“动感地带”：不缴月租费，每通话 1 分钟，付话费 0.6 元（本题的通话均指市内通话），若一个月通话 x 分钟，两种方式的费用分别为 1y 元和 2y 元． （1）写出 1y 、 2y 与 x 之间的关系式； （2）一个月内通话多少分钟，两种移动通讯费用相同？ （3）某人估计一个月内通话 300 分钟，应选择哪种移动通信合算些？） 第四章《变量之间的关系》单元测试卷 (满分：120 分，时间：90 分钟) 一、选择题（每题 3 分，共 24 分） 1、骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，因变量是（ ） 图 7 A、沙漠 B、体温 C、时间 D、骆驼 2、长方形的周长为 24cm，其中一边为（其中 0x ），面积为 2cm ，则这样的长方形中与的 关系可以写为（ ） A、 2xy  B、  212 xy  C、   xxy  12 D、  xy  122 3、地表以下的岩层温度随着所处深度的变化而变化，在某个地点与的关系可以由公式 2035  xy 来表示，则随的增大而（ ） A、增大 B、减小 C、不变 D、以上答案都不对 4、如图 1 所示，OA、BA 分别表示甲、乙两名学生运动 的路程与时间的关系图象，图中和分别表示运动路程 和时间，根据图象判断快者的速度比慢者的速度每秒快 （ ） A、2.5 m B、2 m C、1.5 m D、1 m 5、表格列出了一项实验的统计数据，表示皮球从高度落 下时弹跳高度与 下落高的关系，试问下 面的哪个式子能 表示这种关系（单位 cm ） （ ） 、 2db  、 db 2 、 25 db D 、 2 db  6、弹簧挂上物体后会伸长，测得一弹簧的长度 y（cm）与所挂的物体的重量 x（kg）间有下 面的关系： x 0 1 2 3 4 5 y 10 10.5 11 11.5 12 12.5 下列说法不正确的是（ ） A． x 与 y 都是变量，且 x 是自变量，y 是因变量 B． 弹簧不挂重物时的长度为 0cm C． 物体质量每增加 1kg，弹簧长度 y 增加 0.5cm D． 所挂物体质量为 7kg 时,弹簧长度为 13.5cm 7、在关系式 y=3x+5 中，下列说法：①x 是自变量，y 是因变量；②x 的数值可以任意选择； ③y 是变量，它的值与 x 无关；④用关系式表示的不能用图象表示；⑤y 与 x 的关系还可以 用列表法和图象法表示，其中说法正确的是（ ） A、①②⑤ B、①②④ C、①③⑤ D、①④⑤ 8、张大伯出去散步，从家走了 20 min ，到了一个离家 900m 的阅报亭，看了 10 min 报纸后， 用了 15 min 返回到家，如图 2 图象中能表示张大伯离家时间与距离之间关系的是（ ） 50 80 100 150 25 40 50 75 图 1 二、填空题（每题 3 分，共 24 分） 1、表示函数之间的关系常常用 三种方法． 2、重庆市家庭电话月租费为 25 元，市内通话费平均每次为 0.2 元.若莹莹家上个月共打出 市内电话次，那么上个月莹莹家应付费与之间的关系为 ，若你家上个月共 打出市内电话 100 次，那么你家应付费 元． 3、某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置： 排 数 1 2 3 4 … 座位数 50 53 56 59 … 上述问题中，第五排、第六排分别有 个、 个座位；第排有 个座位. 4、正方形的边长为，那么它的面积与之间的关系式为 ． 5、假定甲、乙两人在一次赛跑中，路程与时间的 关系如图 3 所示，那么可以知道： ① 甲、乙两人中先到达终点的是 . ② 乙在这次赛跑中的速度为 m/s. 6、声音在空气中传播的速度 y(m/s)与气温 x(ºC)之 间在如下关系： 3315 3  xy （1）当气温 x=15 ºC 时，声音的速度 y= m/s． （2）当气温 x=22 ºC 时，某人看到烟花燃放 5s 后才听到声音响，则此人与燃放的烟花所在 地相距 m 7、拖拉机工作时，油箱中的余油量（升）与工作时间（时）的关系式为 40 6Q t  ．当 4t  时， Q  _________，从关系式可知道这台拖拉机最多可工作_________小时． 8、一个长方形周长为 12，一边长为，面积随的变化而变化，则与的关系式是_________．当 2x  时， y  _________． 三、解答题 1、下表是佳佳往妹妹家打长途电话的几次收费记载： 时间／分 1 2 3 4 5 6 7 电话费／元 0.6 1.2 1.8 2.4 3.0 3.6 4.2 （1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ （2）你能帮佳佳预测一下，如果她打电话用时间是 10 分钟，则需付多少电话费？ 图 2 图 3 A B C D 2、如图 4，在一个半径为18cm 的圆面上，从中心挖去一个小圆面，当挖去小圆的半径由小 变大时，剩下的一个圆环面积也随之发生变化． （1）在这个变化过程中，自变量、因变量各是什么？ （2）如挖去的圆半径为（cm），圆环的面积（ 2cm ）与的关系式是_________； （3）当挖去圆的半径由 1cm 变化到 9cm 时，圆环面的面积由_________ 2cm 变化到 _________ 2cm ． 3、洪山县从 2000 年开始实施退耕还休，每年退耕还休的面积如下表： 时间／年 2000 2001 2002 2003 2004 2005 面积／亩 350 380 420 500 600 720 ①上表反映的是哪两个变量之间的关系？哪个是自变量？哪个是因变量？ ②从表中可知，随时间的变化，退耕还林面积的变化趋势是什么？ ③从 2000 年到 2005 年底，洪山县已完成退耕还林面积多少亩？ 4、已知长方形的相邻两边的长分别是 cmx 和 4cm ，设长方形的周长为 cmy ． ①试写出长方形的周长与之间的关系式； ②求当长为10cm ，15cm 时的周长； ③求当周长分别为 20cm ，30cm 时的值． 5、小明读七年级，他很想一个人郊外秋游，但妈妈不放心，让他将一天的时间安排做一个 详细计划，于是小明绘制了图 5 交给妈妈，你能根据这幅图想象一下小明的秋游情况吗？ 四、拓广探索（20 分） 1、弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下 表： 物体的质量(kg) 0 1 2 3 4 5 弹簧的长度(cm) 12 12．5 13 13．5 14 14．5 (1) 上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量? (2) 当物体的质量为 3kg 时,弹簧的长度怎样变化? (3) 当物体的质量逐渐增加时,弹簧的长度怎样变化? (4) 如果物体的质量为 xkg,弹簧的长度为 ycm,根据上表写出 y 与 x 的关系式; (5) 当物体的质量为 2.5kg 时,根据(4)的关系式,求弹簧的长度. 图 4 图 5 2、如图 6,长方形 ABCD 的边长分别为 AB=12cm,AD=8cm,点 P、Q 都从点 A 出发，分别沿 AB-CD 运动，且保持 AP=AQ，在这个变化过程中，图中的阴影部分的面积也随之变化． 当 AP 由 2cm 变到 8cm 时，图中阴影部分的面积是增加了，还是减少了？增加或减少了多少 平方厘米？ 提升能力 超越自我 1、如图 7，表现了一辆汽车在行驶途中的速度随时间的变化情况． （1）A、B 两点分别表示汽车是什么状态？ （2）请你分段描写汽车在第 0 分到第 19 分的行驶状况． （3）司机休息 5 分钟后继续上路，加速 1 分钟后开始以 60km/h 的速度匀速行驶，5 分钟后 减速，用了 2 分钟汽车停止，请在原图上画出这段时间汽车速度与时间的关系图 2、某中学校长决定带领市级“三好学生”去北京旅游，甲旅行社承诺：“如果校长买全票一 张，则学生可享受半价优惠”；乙旅行社承诺：“包括校长在内所有人按全票的 6 折优惠”．若 全票价为 240 元 （1）设学生数为 x，甲、乙旅行社收费分别为 甲y （元）和 乙y （元），分别写出两个旅行 社收费的表达式． （2）哪家旅行社收费更优惠？ 时间(min) 速度(km/h) 0 30 60 90 120 3 6 9 12 15 18 21 24 27 30 33 A B 图 6 图 7