北师大版数学七年级下册第三章《变量之间的关系》单元检测1 5页

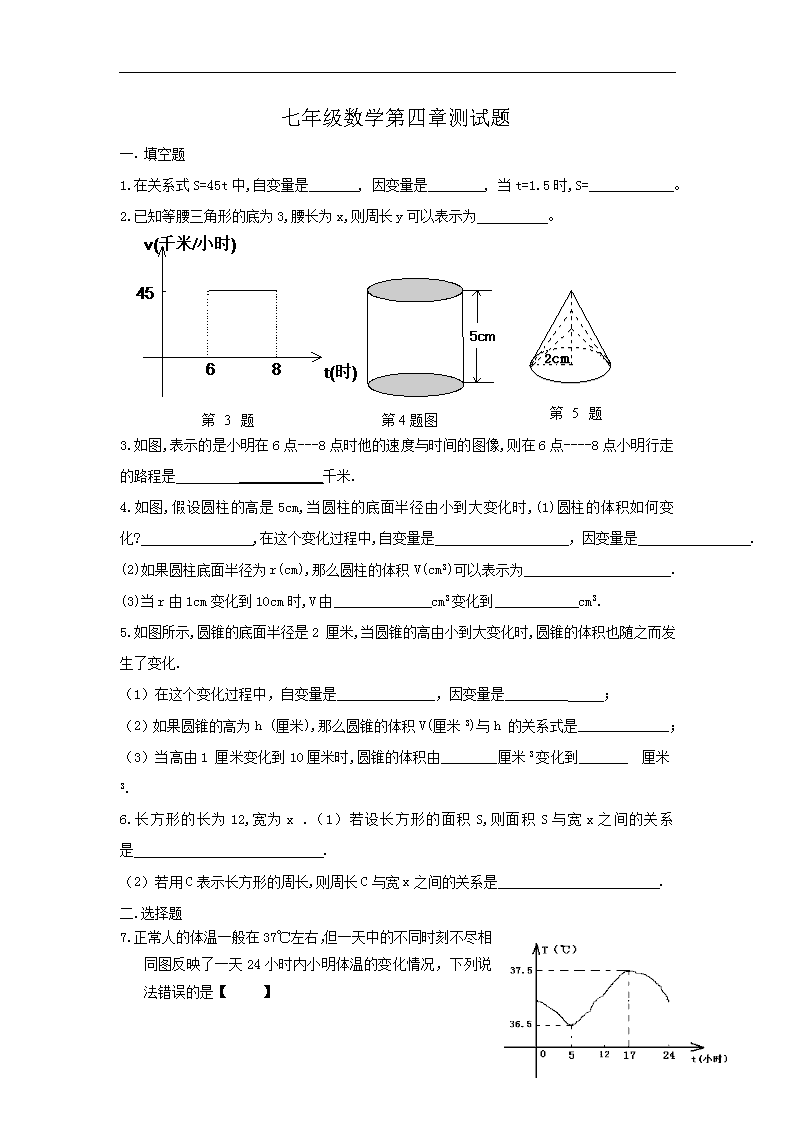
七年级数学第四章测试题 一. 填空题 1.在关系式S=45t中,自变量是 , 因变量是 , 当t=1.5时,S= 。 2.已知等腰三角形的底为 3,腰长为 x,则周长 y 可以表示为 。 45 6 8 v(千米/小时) t(时) 5cm 3.如图,表示的是小明在 6 点---8 点时他的速度与时间的图像,则在 6 点----8 点小明行走的 路程是 ____________千米. 4.如图,假设圆柱的高是 5cm,当圆柱的底面半径由小到大变化时,(1)圆柱的体积如何变 化? ,在这个变化过程中,自变量是 ，因变量 是 . (2)如果圆柱底面半径为 r(cm),那么圆柱的体积 V(cm3)可以表示为 . (3)当 r 由 1cm 变化到 10cm 时,V 由 cm3 变化到 cm3. 5.如图所示,圆锥的底面半径是 2 厘米,当圆锥的高由小到大变化时,圆锥的体积也随之而 发生了变化. （1）在这个变化过程中，自变量是______________，因变量是_________ ； （2）如果圆锥的高为 h (厘米),那么圆锥的体积 V(厘米 3)与 h 的关系式是_____________； （3）当高由 1 厘米变化到 10 厘米时,圆锥的体积由________厘米 3 变化到_______ 厘米 3. 6.长方形的长为 12,宽为 x .（1）若设长方形的面积 S,则面积 S 与宽 x 之间的关系 是 . （2）若用 C 表示长方形的周长,则周长 C 与宽 x 之间的关系是 . 二.选择题 7.正常人的体温一般在 37℃左右，但一天中的不同时刻不尽 相同图反映了一天 24 小时内小明体温的变化情况，下列 说法错误．．的是【 】 第3题图 第 4 题图 第5题图 A．清晨 5 时体温最低 B．下午 5 时体温最高 C．这一天中小明体温 T(单位：℃)的范围是 36.5≤T≤37.5 D．从 5 时至 24 时，小明体温一直是升高的。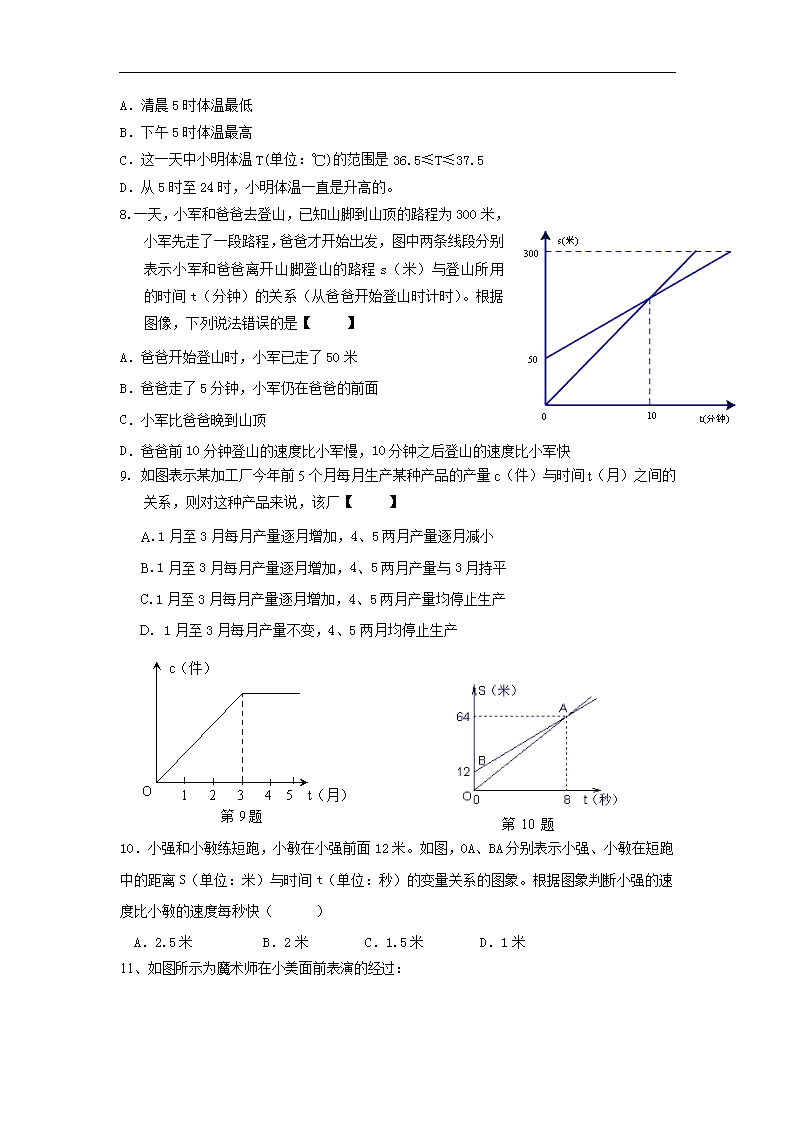 8.一天，小军和爸爸去登山，已知山脚到山顶的路程为 300 米， 小军先走了一段路程，爸爸才开始出发，图中两条线段分别 表示小军和爸爸离开山脚登山的路程 s（米）与登山所用的 时间 t（分钟）的关系（从爸爸开始登山时计时）。根据图 像，下列说法错误．．的是【 】 A．爸爸开始登山时，小军已走了 50 米 B．爸爸走了 5 分钟，小军仍在爸爸的前面 C．小军比爸爸晚到山顶 D．爸爸前 10 分钟登山的速度比小军慢，10 分钟之后登山的速度比小军快 9. 如图表示某加工厂今年前 5 个月每月生产某种产品的产量 c（件）与时间 t（月）之间的 关系，则对这种产品来说，该厂【 】 A.1 月至 3 月每月产量逐月增加，4、5 两月产量逐月减小 B.1 月至 3 月每月产量逐月增加，4、5 两月产量与 3 月持平 C.1 月至 3 月每月产量逐月增加，4、5 两月产量均停止生产 D. 1 月至 3 月每月产量不变，4、5 两月均停止生产 10．小强和小敏练短跑，小敏在小强前面 12 米。如图，OA、BA 分别表示小强、小敏在短跑 中的距离 S（单位：米）与时间 t（单位：秒）的变量关系的图象。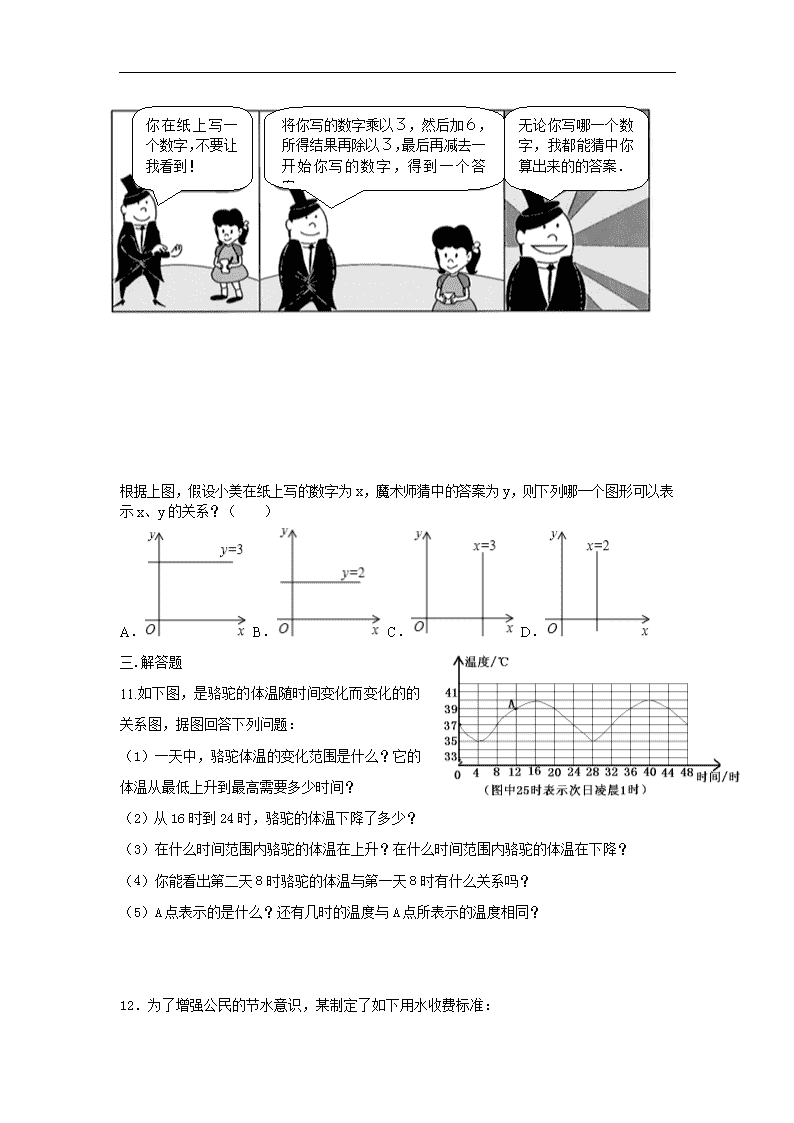根据图象判断小强的速 度比小敏的速度每秒快（ ） A．2.5 米 B．2 米 C．1.5 米 D．1 米 11、如图所示为魔术师在小美面前表演的经过： 第 9 题 1 2 3 4 5 t（月）O c（件） O B A t（秒） S（米） 0 12 64 8 第 10 题 图 根据上图，假设小美在纸上写的数字为 x，魔术师猜中的答案为 y，则下列哪一个图形可以表 示 x、y 的关系？（ ） A． B． C． D． 三.解答题 11.如下图，是骆驼的体温随时间变化而变化的的 关系图，据图回答下列问题： （1）一天中，骆驼体温的变化范围是什么？它的 体温从最低上升到最高需要多少时间？ （2）从 16 时到 24 时，骆驼的体温下降了多少？ （3）在什么时间范围内骆驼的体温在上升？在什么时间范围内骆驼的体温在下降？ （4）你能看出第二天 8 时骆驼的体温与第一天 8 时有什么关系吗？ （5）A 点表示的是什么？还有几时的温度与 A 点所表示的温度相同？ 12．为了增强公民的节水意识，某制定了如下用水收费标准： 无论你写哪一个数 字，我都能猜中你 算出来的的答案． 将你写的数字乘以３，然后加６， 所得结果再除以３，最后再减去一 开始你写的数字，得到一个答案． 你在纸上写一 个数字，不要让 我看到！ 用水量（吨） 水费（元） 不超过 10 吨 每吨 1.2 元 超过 10 吨 超过的部分按每吨 1.8 元收费 （1）该市某户居民 5 月份用水 x 吨（x＞10），应交水费 y（元）应表示为 ； （2）如果该户居民交了 30 元的水费，你能帮他算算实际用了多少的水吗？ 13.某蓄水池开始蓄水，每时进水 20 米 3，设蓄水量为 V（米 3），蓄水时间为 t（时） （1）V 与 t 之间的关系式是什么？ （2）用表格表示当 t 从 2 变化到 8 时（每次增加 1），相应的 V 值？ （3）若蓄水池最大蓄水量为 1000 米 3，则需要多长时间能蓄满水？ （4）当 t 逐渐增加时，V 怎样变化？说说你的理由。 解：（1） （2） 14.一农民朋友带了若干千克的土豆进城出售，为 了方 便，他带了一些零钱备用.按市场售出一些后，又降价出 售.售出土豆千克数 x 与他手中持有的钱数 y（含备用零 钱）的关系如下图所示，结合图像回答下列问题： （1）农民自带的零钱是多少？ （2）降价前他每千克土豆出售的价格是多少？ （3）降价后他按每千克 0.4 元将剩余的土豆售完，这时 他手中的钱（含备用的钱）是 26 元，问他一共带了多少 千克的土豆？ 30 10 5 0 26 20 x（千克） y（元） 第 14 题 15.如图所示，在一个边长为 12cm 的正方形的四个角都剪去一个大小相等的小正方形，当小 正方形的边长由小到大变化时，图中阴影部分的面积也随之发生变化。 （1）在这个变化过程在，自变量、因变量各是什么？ （2）如果小正方形的边长为 xcm，图中阴影部分的面积为 ycm2,写出 y 与 x 的关系式； （3）当小正方形的边长由 1cm 变化到 5cm 时，阴影部分的面积是怎样变化的？ 16、如图 1 是甲、乙两个圆柱形水槽的轴截而示意图，乙槽中有一圆柱形铁块立放其中（圆 柱形铁块的下底面完全落在乙槽底面上）．现将甲槽中的水匀速注人乙槽，甲、乙两个 水槽中水的深度 y（厘米＞与注水时间 x（分钟）之间的关系如图 2 所示．根据图象提 供的信息，解答下列问题： （1）图 2 中折线 ABC 表示 槽中水的深度与注水时间之间的关系，线段 DE 表示 槽中水的深度与注水时间之间的关系（以上两空选塡“甲”或“乙”），点 B 的纵 坐标表示的实际意义是 （2）注水多长时间时，甲、乙两个水槽中水的深度相同？ （3）若乙槽底面积为 36 平方厘米（壁厚不计），求乙槽中铁块的体积；