浙教版七年级数学下册第1章平行线检测卷（新版） 7页

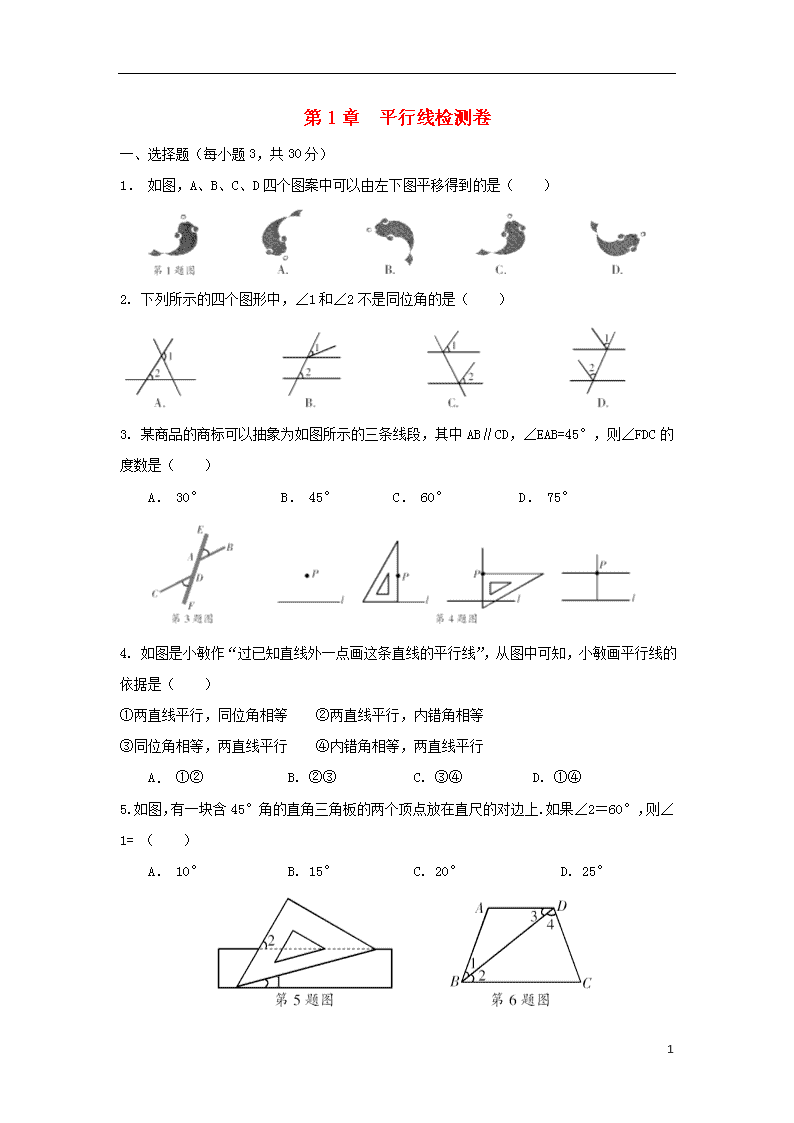
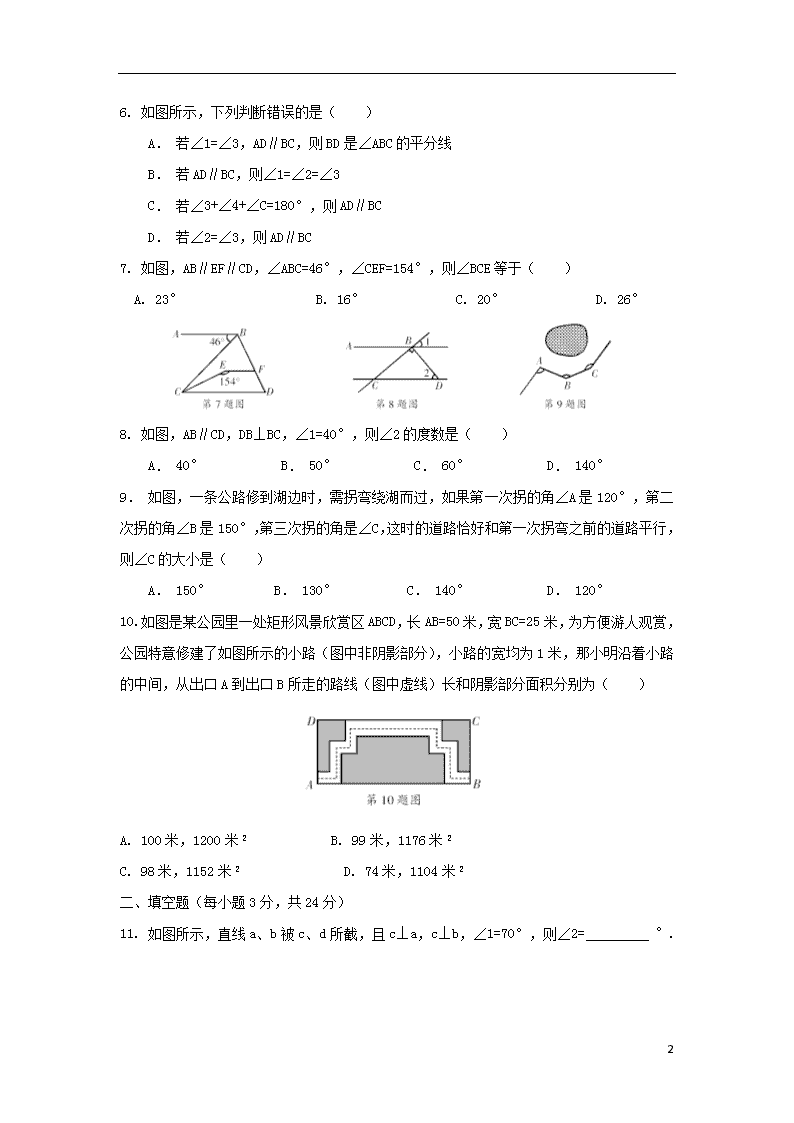
1 第 1 章 平行线检测卷 一、选择题（每小题 3，共 30 分） 1． 如图，A、B、C、D 四个图案中可以由左下图平移得到的是（ ） 2. 下列所示的四个图形中，∠1 和∠2 不是同位角的是（ ） 3. 某商品的商标可以抽象为如图所示的三条线段，其中 AB∥CD，∠EAB=45°，则∠FDC 的 度数是（ ） A． 30° B． 45° C． 60° D． 75° 4. 如图是小敏作“过已知直线外一点画这条直线的平行线”，从图中可知，小敏画平行线的 依据是（ ） ①两直线平行，同位角相等 ②两直线平行，内错角相等 ③同位角相等，两直线平行 ④内错角相等，两直线平行 A． ①② B. ②③ C. ③④ D. ①④ 5. 如图，有一块含 45°角的直角三角板的两个顶点放在直尺的对边上. 如果∠2＝60°， 则∠1= （ ） A． 10° B. 15° C. 20° D. 25° 2 6. 如图所示，下列判断错误的是（ ） A． 若∠1=∠3，AD∥BC，则 BD 是∠ABC 的平分线 B． 若 AD∥BC，则∠1=∠2=∠3 C． 若∠3+∠4+∠C=180°，则 AD∥BC D． 若∠2=∠3，则 AD∥BC 7. 如图，AB∥EF∥CD，∠ABC=46°，∠CEF=154°，则∠BCE 等于（ ） A. 23° B. 16° C. 20° D. 26° 8. 如图，AB∥CD，DB⊥BC，∠1=40°，则∠2 的度数是（ ） A． 40° B． 50° C． 60° D． 140° 9． 如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角∠A 是 120°，第二 次拐的角∠B 是 150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行， 则∠C 的大小是（ ） A． 150° B． 130° C． 140° D． 120° 10. 如图是某公园里一处矩形风景欣赏区 ABCD，长 AB=50 米，宽 BC=25 米，为方便游人观 赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为 1 米，那小明沿着 小路的中间，从出口 A 到出口 B 所走的路线（图中虚线）长和阴影部分面积分别为（ ） A. 100 米，1200 米 2 B. 99 米，1176 米 2 C. 98 米，1152 米 2 D. 74 米，1104 米 2 二、填空题（每小题 3 分，共 24 分） 11. 如图所示，直线 a、b 被 c、d 所截，且 c⊥a，c⊥b，∠1=70°，则∠2= °. 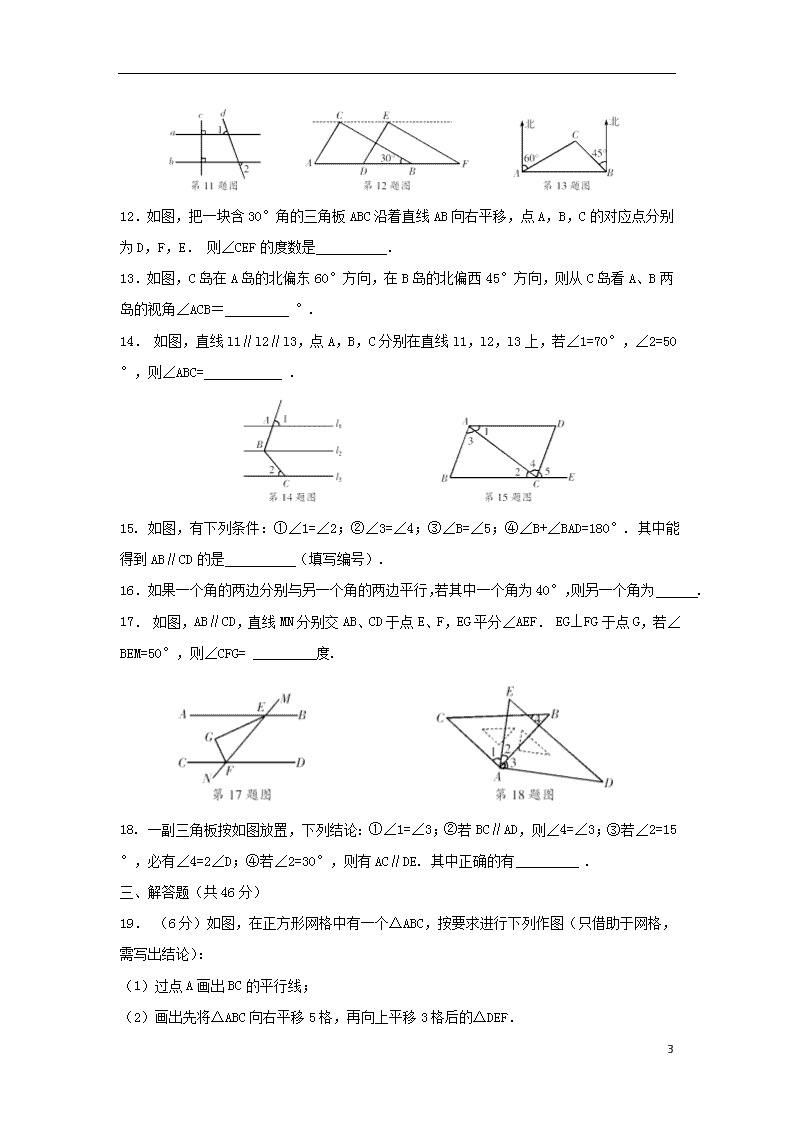3 12． 如图，把一块含 30°角的三角板 ABC 沿着直线 AB 向右平移，点 A，B，C 的对应点分 别为 D，F，E． 则∠CEF 的度数是 ． 13． 如图，C 岛在 A 岛的北偏东 60°方向，在 B 岛的北偏西 45°方向，则从 C 岛看 A、B 两岛的视角∠ACB＝ °. 14． 如图，直线 l1∥l2∥l3，点 A，B，C 分别在直线 l1，l2，l3 上，若∠1=70°，∠2=50°， 则∠ABC= ． 15. 如图，有下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠5；④∠B+∠BAD=180°. 其中能 得到 AB∥CD 的是 （填写编号）. 16． 如果一个角的两边分别与另一个角的两边平行，若其中一个角为 40°，则另一个角 为 . 17． 如图，AB∥CD，直线 MN 分别交 AB、CD 于点 E、F，EG 平分∠AEF． EG⊥FG 于点 G，若 ∠BEM=50°，则∠CFG= 度. 18. 一副三角板按如图放置，下列结论：①∠1=∠3；②若 BC∥AD，则∠4=∠3；③若∠2=15°， 必有∠4=2∠D；④若∠2=30°，则有 AC∥DE. 其中正确的有 . 三、解答题（共 46 分） 19． （6 分）如图，在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格， 需写出结论）： （1）过点 A 画出 BC 的平行线； 4 （2）画出先将△ABC 向右平移 5 格，再向上平移 3 格后的△DEF． 20． （6 分）如图，已知 CD⊥DA，DA⊥AB，∠1=∠2. 试说明 DF∥AE. 请你完成下列填空， 把解答过程补充完整. 解：（1）∵CD⊥DA，DA⊥AB，∴∠CDA=90°，∠DAB=90°（ ）. ∴∠CDA=∠DAB（等量代换）. 又∠1=∠2， 从而∠CDA-∠1=∠DAB- （等式的性质）. 即∠3= . ∴DF∥AE（ ）. 21. （6 分）如图，AB∥CD，BF∥CE，则∠B 与∠C 有什么关系？请说明理由. 22. （8 分）如图，l1∥l2，∠α是∠β的 2 倍，求∠α的度数． 5 23. （8 分）如图，已知 AC⊥BC，DE⊥AC. （1）若 FH⊥AB，∠1 与∠2 互补，则 CD⊥AB 吗？请说明理由； （2）若 DC 是∠BDE 的平分线，∠1=α，求∠BAC（用关于α的代数式表示）. 24. （12 分）如图，直线 AC∥BD，连结 AB，线段 AB、直线 BD、直线 AC 把平面分成①、②、 ③、④四个部分，规定：线上各点不属于任何部分. 当动点 P 落在某个部分时，连结 PA、 PB 构成∠PAC、∠APB、∠PBD 三个角. （提示：有公共端点的两条重合的射线组成的角是 0 度角） （1）当动点 P 落在第①部分时，请说明∠APB＝∠PAC＋∠PBD； （2）当动点 P 落在第②部分时，∠APB＝∠PAC＋∠PBD 是否成立； （3）当动点 P 落在第③部分时，全面探究∠APB、∠PAC、∠PBD 之间的关系，并写出动点 P 的具体位置和相应的结论. 选择一种结论加以说明. 6 参考答案 第 1 章 平行线检测卷 一、选择题 1—5. CCBCB 6—10. BCBAC 二、填空题 11. 70 12. 150° 7 13. 105 14. 120° 15. ②③ 16. 40°或 140° 17. 65 18. ①③④ 三、解答题 19. 略 20. 垂直的意义 ∠2 ∠4 内错角相等，两直线平行 21. ∠B 与∠C 互补. ∵AB∥CD，∴∠B+∠2=180°. ∵BF∥CE，∴∠C=∠2，∴∠B+∠ C=180°. 22. ∵l1∥l2，∴∠1+∠α=180°. ∵∠1=∠β，∴∠α+∠β=180°. ∵∠α=2∠β， ∴2∠β+∠β=180°，∴∠β=60°，∴∠α=2∠β=120°. 23.（1）∵AC⊥BC，DE⊥AC，∴DE∥BC，∴∠1=∠DCB. ∵∠1+∠2=180°，∴∠DCB+∠2=180°， ∴DC∥FH. ∵FH⊥AB，∴DC⊥AB. （2）∵DC 平分∠BDE，∴∠BDE=2∠1=2α，∴∠ADE=180°-2α. ∵DE⊥AC，∴∠AED=90°， ∴∠BAC=180°-90°-（180°-2α）=2α-90°. 24. （1）过 P 作 PE∥AC. ∵AC∥BD，∴PE∥BD. ∴∠PAC=∠APE，∠PBD=∠BPE，∴∠PAC+ ∠PBD=∠APE+∠BPE=∠APB，即∠APB=∠PAC+∠PBD. （2）不成立，这时应该是∠PAC+∠PBD+∠APB=360°. （3）①当 P 在直线 AB 左侧时，∠APB=∠PAC-∠PBD，设 PB 交 AC 于点 E. ∵AC∥BD，∴∠ PEC=∠PBD. ∵∠APB+∠PEC+∠PAE=180°，∠PAE=180°-∠PAC，∴∠APB+∠PBD+（180°- ∠PAC）=180°，∴∠APB=∠PAC-∠PBD. ②当 P 在直线 AB 上时，∠APB=∠PAC-∠PBD， ∠APB=0°，∵AC∥BD，∴∠PAC=∠PBD，∴∠APB=∠PAC-∠PBD=0°. ③当点 P 在直线 AB 右侧时，∠APB=∠PBD-∠PAC，设 PB 交 AC 于点 F. ∵AC∥BD，∴∠PFC=∠PBD. ∵∠APB+∠ PAC+∠PFA=180°，∠PFA=180°-∠PFC=180°-∠PBD，∴∠APB+∠PAC+（180°-∠PBD） =180°，∴∠APB=∠PBD-∠PAC. 综上所述，∠APB= PBDPAC  .