2019七年级数学上册 第6章 图形的初步知识 6角的大小比较 6页

‎6.6　角的大小比较 ‎1．如果两个角的____________，那么我们就说这两个角相等．‎ ‎2．如果两个角的____________，那么我们就说度数较大的角较大．‎ ‎3．____________的角是直角，____________的角是锐角，____________的角是钝角．‎ A组　基础训练 ‎1．下列各角中，不是钝角的是(　　)‎ A.周角 B.平角 C.直角 D.平角 ‎2．两条射线把一个平角分成1∶2∶3三部分，这三部分中，最大的一部分等于(　　)‎ A．80° B．90° C．100° D．120°‎ ‎3．在∠AOB的内部任取一点C，作射线OC，则一定存在(　　)‎ A．∠AOB>∠AOC B．∠AOB<∠BOC C．∠BOC>∠AOC D．∠AOC>∠BOC ‎4．(连云港中考)已知∠α＝17°18′，∠β＝17.18°，∠γ＝17.3°，下列结论正确的是(　　)‎ A．∠α＝∠β<∠γ B．∠α＝∠β>∠γ C．∠α＝∠γ>∠β D．∠α＝∠γ<∠β ‎5．已知∠ABC与∠MNP，若点B与点N重合，BC与MN重合，且BA在∠MNP的内部，则它们的大小关系是(　　)‎ A．∠ABC>∠MNP B．∠ABC<∠MNP C．∠ABC＝∠MNP D．不能确定 6． 如图，比较下列各角的大小，用”>”或”<”填空：‎ 6‎ 第6题图 ‎(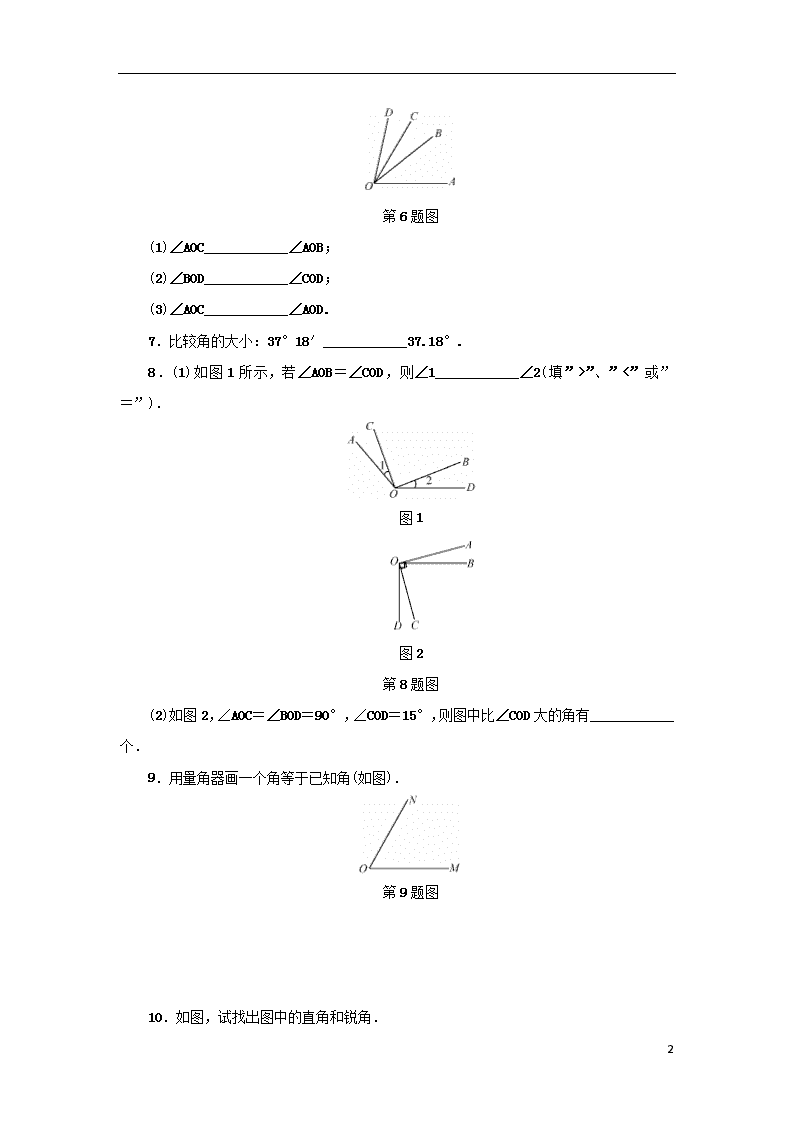1)∠AOC____________∠AOB；‎ ‎(2)∠BOD____________∠COD；‎ ‎(3)∠AOC____________∠AOD.‎ ‎7．比较角的大小：37°18′____________37.18°.‎ ‎8．(1)如图1所示，若∠AOB＝∠COD，则∠1____________∠2(填”>”、”<”或”＝”)．‎ 图1‎ ‎　　　‎ 图2‎ 第8题图 ‎(2)如图2，∠AOC＝∠BOD＝90°，∠COD＝15°，则图中比∠COD大的角有____________个．‎ ‎9．用量角器画一个角等于已知角(如图)．‎ 第9题图 ‎　　　　‎ ‎10．如图，试找出图中的直角和锐角．‎ 6‎ 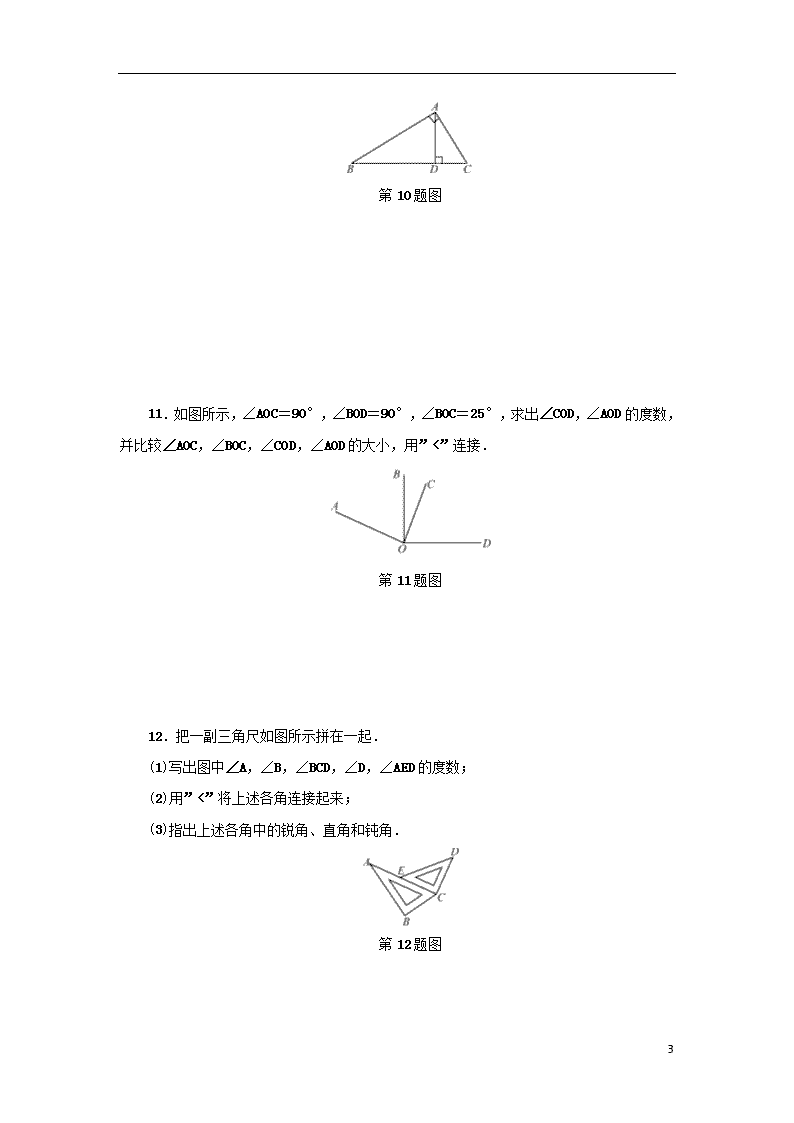第10题图 ‎　　　　‎ ‎11．如图所示，∠AOC＝90°，∠BOD＝90°，∠BOC＝25°，求出∠COD，∠AOD的度数，并比较∠AOC，∠BOC，∠COD，∠AOD的大小，用”<”连接．‎ 第11题图 ‎　　　　‎ ‎12．把一副三角尺如图所示拼在一起．‎ ‎(1)写出图中∠A，∠B，∠BCD，∠D，∠AED的度数；‎ ‎(2)用”<”将上述各角连接起来；‎ ‎(3)指出上述各角中的锐角、直角和钝角．‎ 第12题图 ‎　　　　‎ 6‎ B组　自主提高 ‎13．足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在(　　)‎ 第13题图 A．点C B．点D或点E C．线段DE(异于端点)上一点 D．线段CD(异于端点)上一点 ‎14．已知∠α，∠β都是钝角，甲、乙、丙、丁四人计算(∠α＋∠β)的结果依次是28°、48°、60°、88°，其中只有一人计算正确，他是(　　)‎ A．甲 B．乙 C．丙 D．丁 ‎15．已知下列三个时刻1∶20，9∶30，11∶40的时针与分针所成的角分别是∠α，∠β，∠γ.试比较这三个角的大小，并说明理由．‎ ‎　　　　‎ C组　综合运用 ‎16．如图所示，点P为直线l外一点，过点P画直线PA，PB，PC，…，分别交l于点A，B，C，…，请你用量角器量出∠1，∠2，∠3的度数，并比较它们的大小，用”<”连接，‎ 6‎ 再用刻度尺量出PA，PB，PC的长度，并比较它们的大小，用”<”连接．观察角度和长度之间的关系，你发现了什么结论？‎ 第16题图 参考答案 ‎6．6　角的大小比较 ‎【课堂笔记】‎ ‎1．度数相等　2.度数不相等　3.等于90°　小于直角　大于直角而小于平角 ‎【分层训练】‎ ‎1．D　2.B　3.A　4.C　5.B ‎6．(1)>　(2)>　(3)<‎ ‎7．>‎ ‎8．(1)＝　(2)4‎ ‎9．画图略 ‎10．直角：∠ADB，∠ADC，∠BAC.‎ 锐角：∠B，∠C，∠BAD，∠CAD.‎ ‎11．∠COD＝65°，∠AOD＝155°，‎ 6‎ ‎∠BOC<∠COD<∠AOC<∠AOD.‎ ‎12．(1)∠A＝30°，∠B＝90°，∠BCD＝150°，∠D＝45°，∠AED＝135°.‎ ‎(2)∠A<∠D<∠B<∠AED<∠BCD.‎ ‎(3)∠A与∠D是锐角，∠B是直角，∠AED与∠BCD是钝角．‎ ‎13．C　14.B ‎15．∠α＝80°，∠β＝105°，∠γ＝110°，∠α<∠β<∠γ.‎ ‎16．∠1<∠3<∠2，PB