八年级下数学课件八年级下册数学课件《勾股定理》 人教新课标 (4)_人教新课标 37页

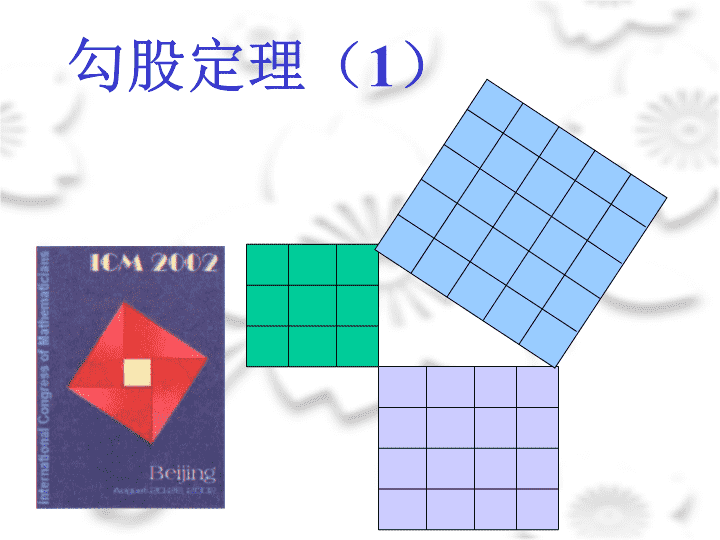
勾股定理人教版八年级（下）第十七章 勾股定理（1） 看一看相传2500年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察下面的图案，看看你能发现什么？ 相传2500年前，毕达哥拉斯有一次在朋友家里做客时，发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系．我们也来观察右图中的地面，看看有什么发现？情景问题 ABCABC（图中每个小方格代表一个单位面积）图2-1图2-2（1）观察图2-1正方形A中含有个小方格，即A的面积是个单位面积。正方形B的面积是个单位面积。正方形C的面积是个单位面积。99918你是怎样得到上面的结果的？与同伴交流交流。 ABCABC（图中每个小方格代表一个单位面积）图2-1图2-2分“割”成若干个直角边为整数的三角形（单位面积） ABCABC（图中每个小方格代表一个单位面积）图2-1图2-2（单位面积）把C“补”成边长为6的正方形面积的一半 ABCABC（图中每个小方格代表一个单位面积）图2-1图2-2（2）在图2-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？（3）你能发现图2-1中三个正方形A，B，C的面积之间有什么关系吗？SA+SB=SC即：两条直角边上的正方形面积之和等于斜边上的正方形的面积 ABC图3-1ABC图3-2分割成若干个直角边为整数的三角形（面积单位）一般的直角三角形三边为边作正方形 ABC图3-1ABC图3-2把C“补”成边长为7的正方形面积加1单位面积的一半（面积单位）思考：面积A，B，C还有上述关系吗？ ABC图3-1ABC图3-2（1）你能用三角形的边长表示正方形的面积吗？（2）你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流。议一议 ABC图1-2ABC图1-32．观察右边两个图并填写下表：A的面积B的面积C的面积图1-2图1-3169254913做一做利用格纸探究 ABCacbSa+Sb=Sc观察所得到的各组数据，你有什么发现？猜想:两直角边a、b与斜边c之间的关系？a2+b2=c2 acb观察所得到的各组数据，你有什么发现？猜想两直角边a、b与斜边c之间的关系？a2+b2=c2Sa+Sb=Sc ┏a2+b2=c2acb命题1：直角三角形两直角边的平方和等于斜边的平方.勾股弦勾股定理(毕达哥拉斯定理) 依据科学理论的证实：我国汉代的数学家赵爽指出：四个全等的直角三角形如下拼成一个中空的正方形。你能用这个图试着证明命题1吗？赵爽弦图cba黄实朱实 ababcabcc2b2a2=+ 赵爽弦图的证法∴c2=a2+b2S大正方形=S小正方形+4S直角三角形C2=（b-a）2+4×cba黄实朱实C2=a2-2ab+b2+2abb-a cabcabcabcab∵(a+b)2=c2+4•ab/2a2+2ab+b2=c2+2ab∴a2+b2=c2大正方形的面积可以表示为；也可以表示为(a+b)2c2+4•ab/2 两千多年前，古希腊有个哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派，1955勾股世界国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。 在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.勾股abc勾股 1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做625576144169 做一做：P62540026xP的面积=______________X=____________225BACAB=__________AC=__________BC=__________251520 比一比看看谁算得快！2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做 11美丽的勾股树 １、如图,一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为()A.3米B.4米C.5米D.6米C３４ ２、湖的两端有A、Ｂ两点，从与ＢA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为()ABCA.50米B.120米C.100米D.130米130120?A 如图，大风将一根木制旗杆吹裂，随时都可能倒下，十分危急。接警后“119”迅速赶到现场，并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域，那么你能确定这个安全区域的半径至少是多少米吗？议一议：9m24m? 1876年4月1日，伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年，伽菲尔德就任美国第20任总统。后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统证法”。 无字证明青出朱方青方朱入朱出青入青入青出青出 abc无字证明①②③④⑤ 青出朱入朱出朱方青方青入青入青出青出华罗庚青朱出入图朱入朱出 对比两个图形,你能直接观察验证出勾股定理吗？两幅图中彩色的四个直角三角形总面积呢？提示：图中的两个大正方形面积相等吗？空白部分的面积呢？那剩余的 小结①本节课学到了什么数学知识？②你了解了勾股定理的发现方法了吗？③你还有什么困惑？作业教材第77页习题18.1第1、2、3题 谢谢！再见！