八年级下数学课件八年级下册数学课件《三角形的中位线》 北师大版 (9)_北师大版 13页

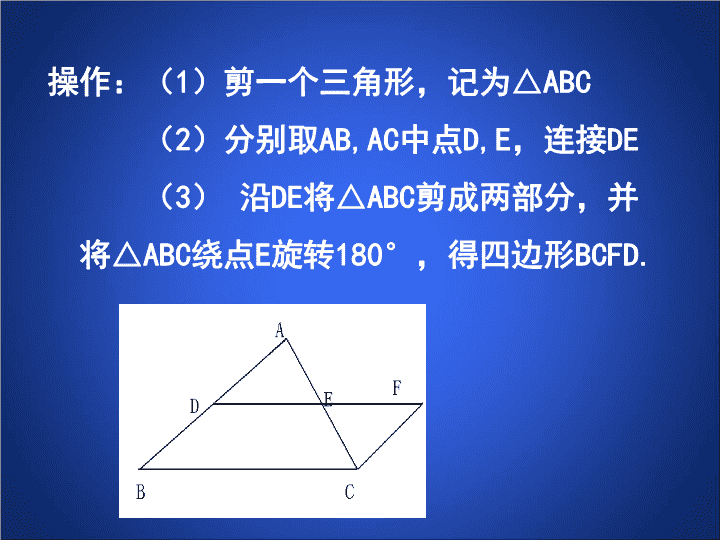
第六章平行四边形3三角形的中位线 创设情景，导入课题思考：怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？ 操作：（1）剪一个三角形，记为△ABC（2）分别取AB,AC中点D,E，连接DE（3）沿DE将△ABC剪成两部分，并将△ABC绕点E旋转180°，得四边形BCFD. 2、思考：四边形BCFD是平行四边形吗？3、探索新结论：若四边形BCFD是平行四边形，那么ＤＥ与ＢＣ有什么位置和数量关系呢？ 三角形的中位线：连接三角形两边中点的线段叫做三角形的中位线。ABCDE三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半.几何表示：∵DE是△ABC的中位线∴DE∥BC,DE=1／2BC教师讲授，传授新知 师生共析，证明定理已知：如图6-20（1），DE是△ABC的中位线.求证:DE∥BC,DE=1／2BC证明:如图6-20(2),延长DE到F,使DE=EF,连接CF.在△ADE和△CFE中∵AE=CE,∠1=∠2,DE=FE∴△ADE≌△CFE∴∠A=∠ECF,AD=CF∴CF∥AB∵BD=AD∴BD=CF∴四边形DBCF是平行四边形∴DF∥BC,DF=BC∴DE∥BC,DE=1／2BC 灵活运用，自我检测如图,任意画一个四边形，顺次连结四边形四条边的中点，所得的四边形有什么特点？请证明你的结论，并与同伴交流。 已知：在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，如图4-94．求证：四边形EFGH是平行四边形．分析：已知四条线段的中点，可设法应用三角形中位线定理，找到四边形EFGH的边之间的关系．而四边形ABCD的对角线可以把四边形分成两个三角形，所以添加辅助线，连结AC或BD，构造“三角形的中位线”的基本图形． 练一练:1、A、B两点被池塘隔开，在没有任何测量工具的情况下，小明通过下面的方法估测出了A,B间的距离：在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN=20m，那么A、B两点的距离是多少？为什么？2．已知:三角形的各边分别为6cm,8cm,10cm，则连结各边中点所成三角形的周长为cm,面积为cm2,为原三角形面积的。 3.如图，在四边形ABCD中，E、F、G、H分别是AB、CD、AC、BD的中点。四边形EGFH是平行四边形吗？请证明你的结论。 回顾小结，共同提升小结：（1）这节课学习了哪些具体内容？（2）用什么思维方法提出猜想的？（3）应注意哪些概念之间的区别？ 分层作业，拓展延伸C组习题6.61,2,3题B组习题6.6问题解决第4题 谢谢！