八年级上数学课件《探索三角形全等的条件》 (4)_苏科版 21页

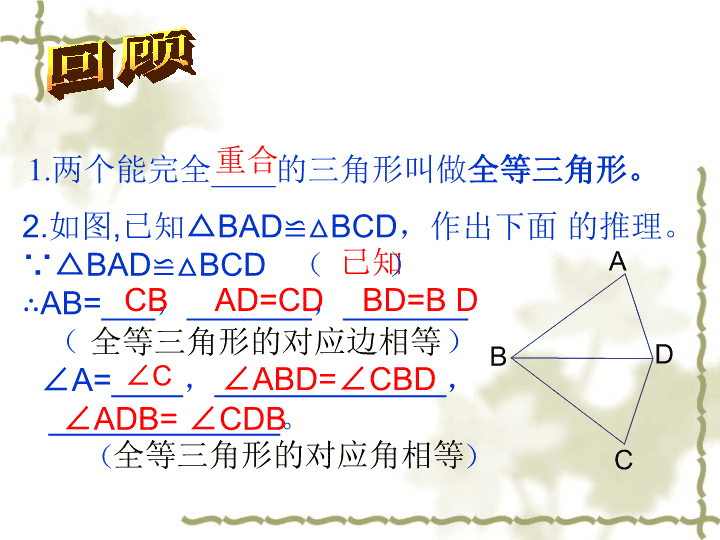
1.3探索三角形全等的条件（1）—SAS（边角边） 回顾1.两个能完全____的三角形叫做全等三角形。重合已知2.如图,已知△BAD≌△BCD，作出下面的推理。∵△BAD≌△BCD（）∴AB=___，_______，_______（）∠A=____，_____________，_____________。（）CBAD=CDBD=BD全等三角形的对应边相等∠C∠ABD=∠CBD∠ADB=∠CDB全等三角形的对应角相等 创设情景小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,小明在另一块没打破的三角形玻璃上该测量哪些数据呢?聪明的你知道吗？ 议一议：(1)只给一个条件：当两个三角形只有1组边或角相等时，它们全等吗？一个角对应相等的两个三角形不一定全等；一条边对应相等的两个三角形不一定全等； 议一议：(2)给出两个条件：当两个三角形有2组边或角相等时，有几种可能的情况？每种情况下作出的三角形全等吗？分别按照下面的条件做一做.①三角形的两个内角分别为30°和50°②三角形的两条边分别为6cm、10cm.③三角形的一个内角为30°，一条边为8cm. 两个角对应相等的两个三角形不一定全等；两条边对应相等的两个三角形不一定全等；一个角和一条边对应相等的两个三角形不一定全等； 我们通过画图、观察、比较知道，只给出一个条件或两个条件时，都不能保证所画出的三角形一定全等.结论 共有4种情况三角形共有6个元素(3条边、3个角)两边一角两角一边边边边角角角两边和它的夹角两边和其中一边的对角议一议：(3)如果给出三个条件:当两个三角形有3组边或角相等时，有几种可能的情况？ 有两条边和它们的夹角对应相等的两个三角形一定全等吗？研究下面的两个三角形：\ ③①活动二：观察下图中的三角形，猜一猜，哪两个三角形是全等三角形？仔细观察②和④，发现他们有什么特征？有两边和其中一边的对角对应相等的两个三角形不一定全等。 拿出按下列步骤画好的三角形1.画∠MAN=50O；2.在AM上截取AB=8cm；在AN上截取AC=6cm；3.连接BC。剪下所得的△ABC，与周围同学所剪的比较一下，它们全等吗？BCAMN50O′活动三: 有________________对应相等的两个三角形全等,简写成_______________我们把这个事实作为两个三角形全等的一个判定方法ABCA’B’C’归纳两边和它们的夹角“边角边”或“SAS”在书写时要注意：1.两个三角形的对应顶点需按同一顺序写2.三个条件按公理名称边-角-边的次序写，3.三个条件中等号两侧分别写同一个三角形的已知元素。 例1如图：AB=AD，∠BAC=∠DAC，△ABC和△ADC全等吗？为什么？解：∵在△ABC和△ADC中AB=AD(已知)∠BAC=∠DAC（已知）AC=AC(公共边)∴△ABC≌△ADC(SAS) 1.如图：AB=AC，AD=AE，△ABE和△ACD全等吗？请说明理由。练一练：解：∵在△ABE和△ACD中AB=AC（已知）∠BAE=∠CAD（公共角）AE=AD（已知）∴△ABE≌△ACD(SAS) 2.已知：如图,AD∥BC，AD=BC问：△ABC和△CDA全等吗？请说明理由。解:∵AD∥BC∴∠1=∠2在△ABC和△CDA中AD=BC(已知)∠1=∠2（已证）AC=CA（公共边）∴△ABC≌△CDA(SAS)12 如图：AD∥BC，AD=BC,AE=CF试说明:(1)△AFD≌△CEB(2)BE∥DF延伸与提高 解:(1)∵AD∥BC∴∠1=∠2∵AE=CF∴AE+EF=CF+EF即AF=CE在△AFD和△CEB中AD=BC∠1=∠2AF=CE∴△AFD≌△CEB(SAS)12(2)∵△AFD≌△CEB(已证)∴∠BEC=∠DFE∴BE∥DF 说一说这节课你学到了什么？ 如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看．AB实践与应用 小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离．请你说明理由．ECADB BECAD∴△ACB≌△DCE(SAS)在△ACB和△DCE中AC=DC∠ACB=∠DCEBC=EC（对顶角相等）∴AB=DE（全等三角形的对应边相等）