八年级下数学课件八年级下册数学课件《多边形的内角和》 北师大版 (8)_北师大版 17页

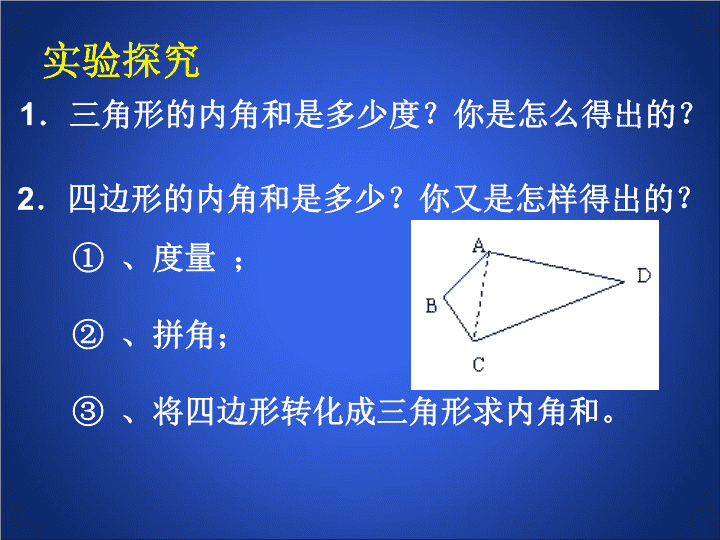
第六章平行四边形4多边形的内角和与外角和(一) 创设现实情境，提出问题1．三角形是如何定义的？2．仿照三角形定义，你能学着给四边形、五边形……边形下定义吗？ 实验探究1．三角形的内角和是多少度？你是怎么得出的？2．四边形的内角和是多少？你又是怎样得出的？①、度量；②、拼角；③、将四边形转化成三角形求内角和。 3．在四边形内角和的探索过程中，用到了几种方法，你认为哪种方法好？请讲述你的理由。4．根据四边形的内角和的求法，你能否求出五边形的内角和呢？ 方法总结： 方法1：如图1，连结AD、AC，五边形的内角和为：3×180°=540°。方法2：如图2，连结AC，则五边形内角和为：360°+180°=540°。方法3：如图3，在AB上任取点F，连FC、FD、FE，则五边形的内角和为：4×180-180°=540°。方法4：如图4，在五边形内任取一点O，连结OA、OB、OC、OD、OE，则五边形内角和为：5×180°-360°=540°。 方法5：如图5，在AB上任取一点F，连结FD，则五边形的内角和为：2×360°-180°=540°。方法6：如图6，在五边开外任取一点O，连结OA、OB、OC、OD、OE，则五边形内角和为：4×180°-180°=540°。小结：纵观以上各种证明思路，其共同点是通过图形分割，把五边形问题转化为熟悉的三角形、四边形问题来解决。 5．小组合作，完成下面的表格：01180°122×180°233×180°344×180°(n-3)(n-2)(n-2)×180° 结论：从多边形的一个顶点可以引出（n-3)条对角线，把n边形分成(n-2)个三角形。从而得出：n边形的内角和是(n-2)·180°。 巩固训练1．如图6-24，四边形ABCD中，∠A+∠C=180°，∠B与∠D有怎样的关系？2．一个多边形的内角和为1440°，则它是几边形？3．一个多边形的边数增加1，则它的内角和将如何变化？ 拓展延伸想一想：观察图中的多边形，它们的边、角有什么特点？正多边形定义：在平面内，每个内角都相等、每条边也都相等的多边形叫做正多边形。 议一议：①一个多边形的边都相等，它的内角一定都相等吗？②一个多边形的内角都相等，它的边一定都相等吗？ 练一练：①正三角形、正四边形（正方形）、正五边形、正六边形、正八边形的内角分别是多少度？②正n边形的内角是多少度？③一个正多边形的每个内角都是150°，求它的边数？ 思维升华议一议:剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流. 知识小结1．过本节课的学习，你学到了哪些知识？有何体会？2．在学习多边形的有关概念时，我们使用了由特殊到一般的数学方法，并运用了类比、转化的思想方法。 作业：C．155页习题6.71,2.3题;B．探究五角星的五个角的度数之和;A.设计一个实验(如剪纸、拼图等），说明四边形的内角和是360°。 谢谢！