八年级下数学课件八年级下册数学课件《二次根式》 人教新课标 (15)_人教新课标 72页

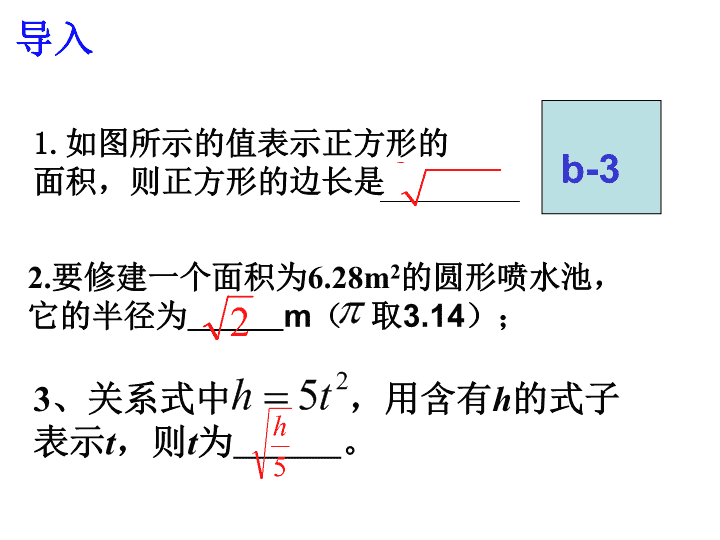
⑵什么是一个数的算术平方根？如何表示？正数的正的平方根叫做它的算术平方根。回忆⑴什么叫做一个数的平方根？如何表示？一般地，若一个数的平方等于a，则这个数就叫做a的平方根。用(a≥0)表示。0的算术平方根平方根是0a的平方根是 复习1、如果，那么；2、如果，那么；3、如果，那么。±2 1.如图所示的值表示正方形的面积，则正方形的边长是b-32.要修建一个面积为6.28m2的圆形喷水池，它的半径为m（取3.14）；3、关系式中，用含有h的式子表示t，则t为。导入 新授:观察以上各式，它们有什么共同特点？表示一些正数的算术平方根 表示一些正数的算术平方根．你认为所得的各代数式有哪些共同特点？被开方数二次根号 归纳:二次根式的定义(默1）一般地，形如的式子叫二次根式。 16.1二次根式 本课学习目标： （1）二次根式的概念(双重非负性)（2）根号内字母的取值范围（3）二次根式的性质(1,2) 请你凭着自己已有的知识,说说对二次根式的认识！?开动你的脑筋,你一定行! 2.a可以是数,也可以是式.3.形式上含有二次根号4.a≥0,≥05.既可表示开方运算,也可表示运算的结果.1.表示a的算术平方根(双重非负性) 如：这类代数式只能称为含有二次根式的代数式，不能称之为二次根式；而这类代数式，应把这些二次根式看做系数或常数项，整个代数式仍看做整式。注意 说一说:下列各式是二次根式吗?(m≤0),(x,y异号)在实数范围内,负数没有平方根火眼金睛 1、判断下列代数式中哪些是二次根式？⑴⑵⑶⑷⑸⑹ 例1x为何值时，下列各式在实数范围内有意义。例题讲解（3）由题意可知：1）由x-5≥0,得x≥5∴当x≥5时，有意义（2）由1-3x≥0得x≤∴当x≤时，有意义∴当-1≤x≤3时，有意义；解：（ 变式：当x取何值时，在实数范围内有意义。（默2）∴当x＞5时，在实数范围内有意义。x-50解：由题意得 5解:由题意得,5555（默3） 求下列二次根式中字母的取值范围（默4）变式：(1)解：字母a的取值范围是全体实数(1)∵无论取何值，都有∴字母的取值范围是全体实数.∴字母的取值范围是全体实数.∵例2(2)变式：(2)解：-(a为任何实数)(a=1)说明:1.当被开方数本身为非负数或能化为非负数形式时，其字母的取值范围为：全体实数；2.当被开方数本身为非正数或能化为非正数形式时，其字母的取值范围为：使被开方数为0的值。(a为任何实数) 求下列二次根式中字母的取值范围：解：（1）由题意得：即当时，有意义.求字母的取值范围的口诀（默5）从左看到右;从上看到下看到分数线,分母不为0（2）(3)为任意实数看到偶次根式,被开方数大于等于0看到0指数,底数不为0最后画数轴,写出解集来 1、x取何值时,下列二次根式有意义?快速口答(7)(8) 参考图1-2,完成以下填空:27性质一:一般地,二次根式有下面的性质:快速判断53a?94161517 一般地，（a≥0）归纳 合作学习请比较左右两边的式子,议一议:与有什么关系?当时,;当时,一般地,二次根式有下面的性质:225500性质二:一般地，根据算术平方根的意义， 大家一起来分辨22-2|-2|=2|2|=2-|-2|=-2 大家抢答 2.从取值范围来看,a≥0a取任何实数1:从运算顺序来看,先开方,后平方先平方,后开方=aa(a≥0)3.从运算结果来看:-a(a＜0)==∣a∣总结规律 比较分析和读法运算顺序a的取值范围运算结果先开方,后平方先平方,后开方a≥0a取全体实数a∣a∣根号a的平方根号下a平方 二次根式的性质及它们的应用:（1）（2）a0-a(a>0)(a=0)(a<0)平方在外面直接去根号平方在里面夹上绝对值分类来讨论口诀（默6） (x﹤y)(x>0)讨论与思考将下列各式化简： 例3、化简及求值：(1)(2)(3)(a＜0,b＞0)其中a=(5) (1)(2)(3)(a＜0,b＞0)其中a=(5) 解：原式==|x-3|+|x+1|∵-10∴原式=(3-x)+(x+1)=4（默7）（默8） 1.若,则x的取值范围为()(A)x≤1(B)x≥1(C)0≤x≤1(D)一切有理数引申—提高A2.实数a、b、c在数轴上的位置如图所示，化简abc 3.已知a，b，c为△ABC的三边长，化简：+-这一类问题注意把二次根式的运算搭载在三角形三边之间的关系这个知识点上，特别要应用好。（默9） 化简4.化简（默10） 归纳二次根式的非负性：二次根式的双重非负性： -13(-5)×2×(-2)=20 3.根据非负数的性质，就可以确定字母的值.2.如果几个非负数的和为零，那么每一个非负数都为零.到现在为止，我们已学过哪些数非负数形式？思考：非负数的性质：1.几个非负数的和、积、商、乘方及算术平方根仍是非负数（默11）（默11）（默11） 例3、当x是怎样的实数时，有最小值？最小值是多少？有什么性质？二次根式的双重非负性：当x=-2时，有最小值02、2+的最小值为＿＿，此时x的值为＿＿。23（默12） 当t是怎样的实数时，有最小值？最小值是多少？当t=0时，有最小值1引申—提高（默13） 小结：1.怎样的式子叫二次根式？2.怎样判断一个式子是不是二次根式？3.如何确定二次根式中字母的取值范围？（1）.形式上含有二次根号（2）.被开方数a为非负数，从左看到右;从上看到下看到分数线,分母不为0看到偶次根式,被开方数大于等于0看到0指数,底数不为0最后画数轴,写出解集来 4.真正理解：这两个性质的概念，我们才能灵活地去解决有关二次根式的问题。解决二次根式类问题时特别注意条件，有时还得挖掘隐含条件。 二次根式的性质及它们的应用:（1）（2）a0-a(a>0)(a=0)(a<0)平方在外面直接去根号平方在里面夹上绝对值分类来讨论口诀 3.根据非负数的性质，就可以确定字母的值.2.如果几个非负数的和为零，那么每一个非负数都为零.到现在为止，我们已学过哪些数非负数形式？思考：非负数的性质：1.几个非负数的和、积、商、乘方及算术平方根仍是非负数 切入点：从字母的取值范围入手。1.已知，你能求出的值吗？3.已知，你能求出a的取值范围吗？2.已知与互为相反数，求、的值.切入点：从代数式的非负性入手。4.已知为一个非负整数，试求非负整数的值切入点：分类讨论思想。探索交流 解:由题意得, 2.已知a,b为实数，且满足，你能求出a及a+b的值吗？若=0，则=_____。3、已知有意义,那A(a,)在象限.二∵由题意知a＜0∴点A(－,＋) 因为难,所以我挑战!12、11、8、3 1、求下列二次根式中字母的取值范围：基础练习（1）（2）（3）（4）(1)解:由题意得,可取全体实数(2)解:由题意得,(3)解:由题意得,(4)解:由题意得, 解:由题意得,综合提高1.求下列各式有意义时的X取值范围：解:由题意得, 当x为怎样的实数时，下列各式有意义？x≥3x≤6∴3≤x≤6x≥1x≤1∴x=1x为任何实数.x为任何实数. 2.数a在数轴上的位置如图,则0-2-11课内练习11.填空 3.实数p在数轴上的位置如图所示，化简 4.若１＜Ｘ＜４，则化简的结果是＿＿＿＿＿5.设a,b,c为△ABC的三边，化简32a+2b+2c 6.x,y取怎样的实数时，下列各式在实数范围内有意义？ 1.（2010·芜湖中考）要使式子有意义，a的取值范围是（）A.a≠0B.a＞-2且a≠0C.a＞-2或a≠0D.a≥-2且a≠0【解析】选D.要使式子有意义，须同时满足a+2≥0，a≠0两个条件，解两个不等式可得a≥-2且a≠0。 2．下列式子一定是二次根式的是（）A．B．C．D．【解析】选C.A中只有当x≤-2时，才是二次根式，故A不一定是二次根式；B中当x≥0时是二次根式，故B不一定是二次根式；C中无论x为何值，x2+2＞0，所以C一定是二次根式；D中当x=0时，不是二次根式，所以D也不正确。 若a.b为实数,且求的值。解:3. 4.．计算：+++…+5.如果+│b-2│=0，求以a、b为边长的等腰三角形的周长。 6.化简：-（）2．分析：本题是化简，说明题中的每一个二次根式均在有意义的范围内，本题有一个隐条件，即2-x≥0,x≤2.7.设等式在实数范围内成立，其中a,x,y是两两不等的实数，求的值。解：∵ 巩固提高：1.分别求下列二次根式中的字母的取值范围（1）（2）（3）2.当x_____时,有意义.=03.化简：=______2a-3b4.要使式子有意义，那么x的取值范围是（）A、x＞0B、x＜0C、x=0D、x≠0C 5.已知,求的值。6.已知，化简：7.已知：，求的值。 练习:1.用心算一算:0.11812 2.计算： 试试你的计算能力:215-5 试试你的计算能力: 把下列各式写成平方差的形式，再在实数范围内分解因式；思路启迪：利用可以把任何一个非负数或非负式子写成完全平方形式． 把下列各式写成平方差的形式，再在实数范围内分解因式； 因为难,所以我挑战!n为2，9，14，17 解:由题意得,