北师大八年级数学（下册）第三章测试卷（附参考答案） 8页

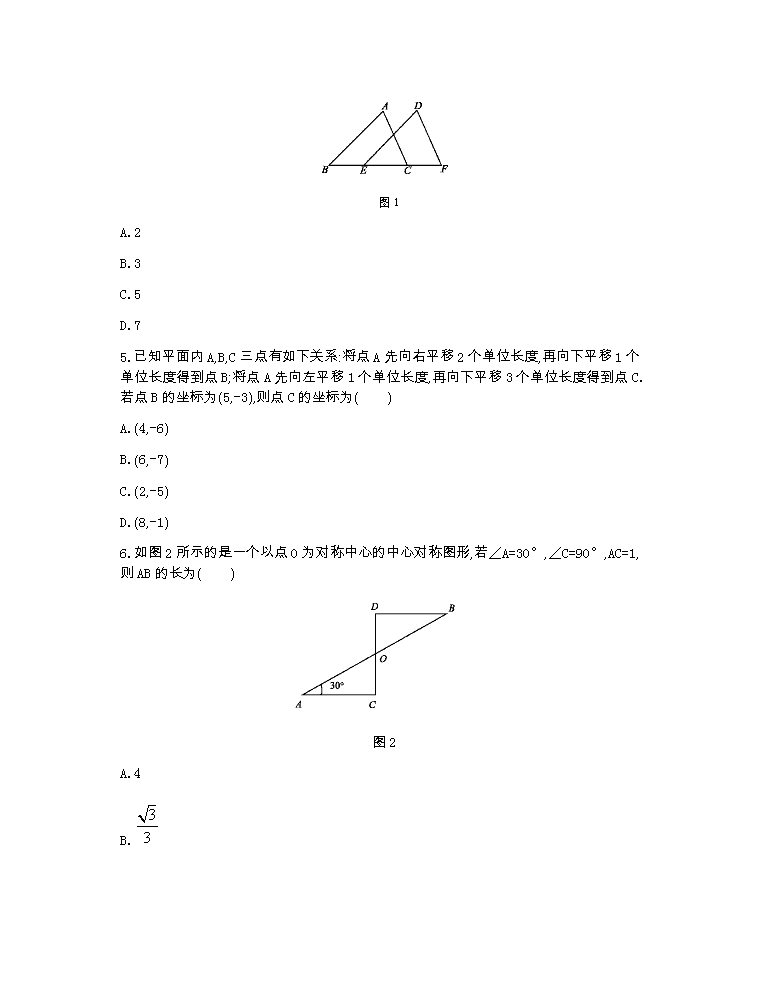
第三章测试卷 （考试时间：90 分钟 满分：100 分） 1.下列现象中,属于平移的是( ) ①温度计中,液柱的上升或下降; ②打气筒打气时,活塞的运动; ③钟摆的摆动; ④传送带上,瓶装饮料的移动. A.②④ B.①③ C.②③ D.①② 2.下列说法正确的是( ) A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小 B.平移和旋转的共同点是改变图形的位置 C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离 D.由平移得到的图形也一定可由旋转得到 3.下列图形中,旋转 120°后能与原图形重合的是( ) A.等边三角形 B.正方形 C.正五边形 D.矩形 4.如图 1,△ABC 沿着由点 B 到点 E 的方向,平移到△DEF,已知 BC=5,EC=3,那么平移的距离 为( ) 图 1 A.2 B.3 C.5 D.7 5.已知平面内 A,B,C 三点有如下关系:将点 A 先向右平移 2 个单位长度,再向下平移 1 个 单位长度得到点 B;将点 A 先向左平移 1 个单位长度,再向下平移 3 个单位长度得到点 C. 若点 B 的坐标为(5,-3),则点 C 的坐标为( ) A.(4,-6) B.(6,-7) C.(2,-5) D.(8,-1) 6.如图 2 所示的是一个以点 O 为对称中心的中心对称图形,若∠A=30°,∠C=90°,AC=1, 则 AB 的长为( ) 图 2 A.4 B. 3 3 C. 2 3 3 D. 4 3 3 7.如图 3 所示,将△ABC 绕点 A 逆时针旋转 80°得到△ADE,连接 BD,则∠ADB 的度数为 ( ) 图 3 A.30° B.50° C.80° D.100° 8.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.如图 4,现有 一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上, 做成一个能绕着小孔平稳旋转的风车.正确的粘合方法是( ) 图 4 A. B. C. D. 9.△A1B1C1 是△ABC 平移后得到的三角形,则△A1B1C1≌△ABC,理由是 . 10.在平面直角坐标系中,点 A(1,2)可由点 B(1,0)向 平移 个单位长度得到. 11.在 26 个大写英文字母中,写出既是轴对称,也是中心对称的字母 、 、 .(写 出 3 个) 12.如图 5,将△ABC 绕点 A 顺时针旋转 60°得到△AED,若线段 AB=3,则 BE= . 图 5 13.如图 6 所示,△ABC 和△DCE 是等边三角形,将△ACE 绕着 点逆时针旋转 度可得 到 . 图 6 14. 如图 7 所示,△ABC 是直角三角形,BC 是斜边,将△ABP 绕点 A 逆时针旋转后,能与△ACP’ 重合,如果 AP=2,那么 PP’= . 图 7 15.作图:(1)如图 8 所示,将字母 A 按箭头所指的方向,平移 3cm,作出平移后的图形;(2)如 图 9 所示,经过平移,△ABC 的顶点 A 移到了点 D,请作出平移后的三角形. 图 8 图 9 16.如图 10 所示的图案可以看成是什么“基本图案”通过怎样的变化得到的? 图 10 17.如图 11 所示,A,B 两点的坐标分别为(2,3),(4,1). (1)求△ABO 的面积; (2)把△ABO 向下平移 3 个单位长度后得到△A’B’O’,求△A’B’O’的 3 个顶点的坐 标. 图 11 18.如图 12 所示,四边形 ABCD 是正方形,AF=AE. (1)可以通过平移、轴对称、旋转中的哪一种方法怎样变化,使△ABE 变到△ADF 的位置? (2)线段 BE 与 DF 之间有怎样的关系,为什么? 图 12 19.如图 13,已知△ABC 三个顶点坐标分别是 A(1,3),B(4,1),C(4,4). (1)请按要求画图: ①画出△ABC 向左平移 5 个单位长度后得到的△A1B1C1; ②画出△ABC 绕着原点 O 顺时针旋转 90°后得到的△A2B2C2. (2)请写出直线 B1C1 与直线 B2C2 的交点坐标. 图 13 20.如图 14①所示,△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共顶点 C,连 接 AF 和 BE. (1)线段 AF 和 BE 有怎样的大小关系?请证明你的结论; (2)将图 14①中的△CEF 绕点 C 旋转一定的角度,得到图 14②,(1)中的结论还成立吗?作出 判断,并说明理由; (3)将图 14①中的△ABC 绕点 C 旋转一定的角度,请你画出一个变换后的图形(草图即可). 此时(1)中的结论还成立吗?作出判断,不必说明理由. ① ② 图 14 参考答案 1.A 2.B 3.A 4.A 5.C 6.D 7.B 8.A 9.平移不改变图形的形状和大小 10.上 2 11.H、I、O 12.3 13.C 60 △BCD 14.2 2 15.解:作图略. 16.解:图案是由△ABC 绕点 O 顺时针(逆时针)旋转三次而形成的,旋转角度依次为 90°,180°,270°. 17.解:(1)S△ABO=3×4- 1 2 ×4×1- 1 2 ×2×2- 1 2 ×2×3=5. (2)△A’B’O’的 3 个顶点的坐标分别为 A’(2,0),B’(4,-2),O’(0,-3). 18.解:(1)旋转方法,△ABE 绕 A 点逆时针旋转 90°,变到△ADF 的位置. (2)BE=DF 且 BE⊥DF.理由如下: 由(1)得△ABE≌△ADF, ∴BE=DF,∠ABE=∠ADF. ∵∠ADF+∠F=90°, ∴∠ABE+∠F=90°,即 BE⊥DF. 19.(1)①如图所示:△A1B1C1 即为所求; ②如图所示:△A2B2C2 即为所求; (2)由图形可知:交点坐标为(-1,-4). 20.解:(1)AF=BE. 证明:∵△ABC 和△CEF 是等边三角形,∴AC=BC,CF=CE, ∠ACF=∠BCE=60 ° . ∴△AFC≌△BEC. ∴AF=BE. (2)成立.理由如下: ∵△ABC 和△CEF 是等边三角形, ∴AC=BC,CF=CE,∠ACB=∠FCE=60 ° . ∴∠ACB-∠FCB=∠FCE-∠FCB, 即∠ACF=∠BCE, ∴△AFC≌△BEC, ∴AF=BE. (3)结论仍成立.作图不唯一,如: