2020八年级数学下册 第17章 勾股定理 3页

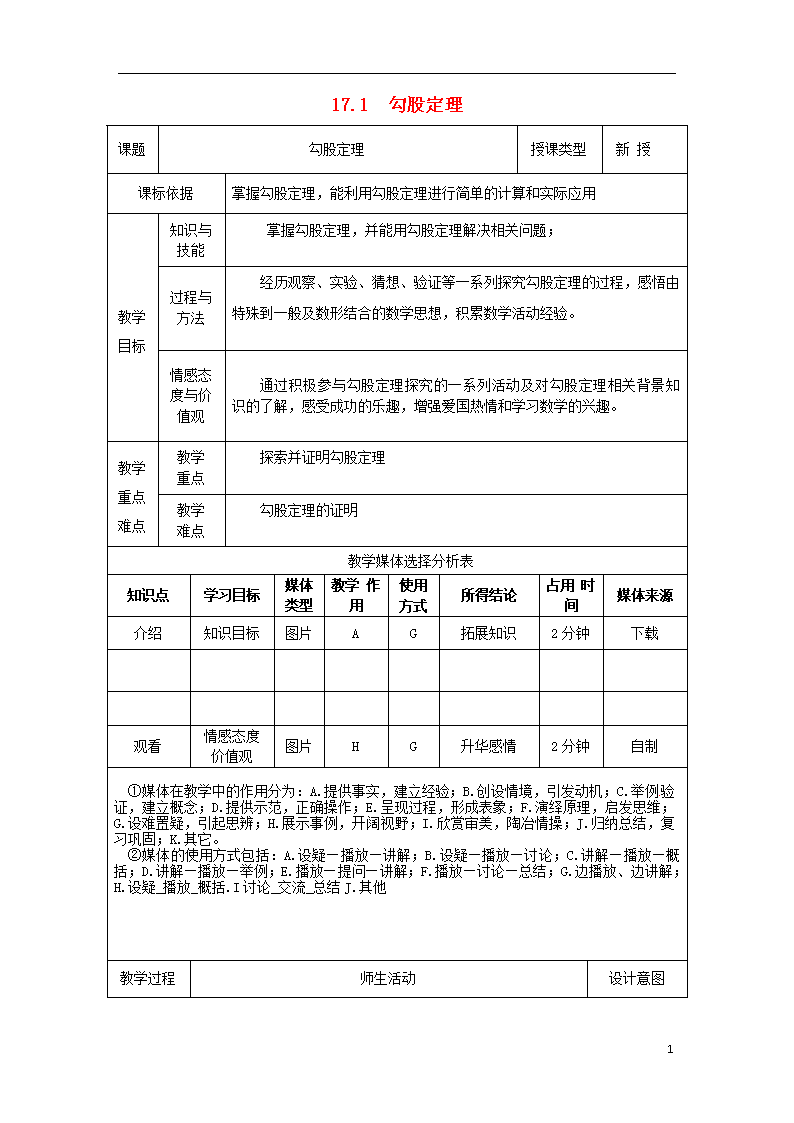
‎17.1 勾股定理 课题 勾股定理 授课类型 新 授 课标依据 掌握勾股定理，能利用勾股定理进行简单的计算和实际应用 教学目标 知识与 技能 掌握勾股定理，并能用勾股定理解决相关问题；‎ 过程与 方法 经历观察、实验、猜想、验证等一系列探究勾股定理的过程，感悟由特殊到一般及数形结合的数学思想，积累数学活动经验。‎ 情感态度与价值观 通过积极参与勾股定理探究的一系列活动及对勾股定理相关背景知识的了解，感受成功的乐趣，增强爱国热情和学习数学的兴趣。‎ 教学重点难点 教学 重点 探索并证明勾股定理 教学 难点 勾股定理的证明 教学媒体选择分析表 知识点 学习目标 媒体类型 教学 作用 使用 方式 所得结论 占用 时间 媒体来源 介绍 知识目标 图片 A G 拓展知识 ‎2分钟 下载 观看 情感态度价值观 图片 H G 升华感情 ‎2分钟 自制 ‎①媒体在教学中的作用分为：A.提供事实，建立经验；B.创设情境，引发动机；C.举例验证，建立概念；D.提供示范，正确操作；E.呈现过程，形成表象；F.演绎原理，启发思维；G.设难置疑，引起思辨；H.展示事例，开阔视野；I.欣赏审美，陶冶情操；J.归纳总结，复习巩固；K.其它。‎ ‎②媒体的使用方式包括：A.设疑—播放—讲解；B.设疑—播放—讨论；C.讲解—播放—概括；D.讲解—播放—举例；E.播放—提问—讲解；F.播放—讨论—总结；G.边播放、边讲解；H.设疑_播放_概括.I讨论_交流_总结J.其他 师生活动 设计意图 3‎ 教学过程设计 一、 创设情境 PPT出示一副2002年在北京召开的第24届国际数学家大会的会徽,教师提问：你见过这个图案吗？它由哪些我们学习过的基本图案组成？‎ 师生活动：‎ 教师引导学生寻找图形中的直角三角形、正方形等，并说明直角三角形的全等关系，指出通过今天的学习，就能理解会徽团的含义。‎ 二、 探究新知 探究1：见PPT，学生观察，发现三个正方形A,B,C的面积有什么关系？‎ 师生活动：学生独立观察图形，分析、思考其中隐含的规律。通过数格子方法或者用割补法将小正方形A,B中的等腰三角形补成一个大正方形，得到结论：小正方形A,B的面积之和等于大正方形C的面积。‎ 追问：由这三个正方形A、B、C的边长构成的等腰直角三角形三条边长之间有怎样的特殊关系？‎ 师生活动：教师引导学生直接由正方形的面积等于边长的平方，归纳出：等腰三角形两条直角边的平方和等于斜边的平方。‎ 探究2：见PPT，在网格中的一般直角三角形，以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系？‎ 师生活动：分别求出A,B,C的面积并寻找它们之间的关系。‎ 追问：正方形A,B,C所围成的直角三角形三条边之间有怎样的特殊关系？‎ 师生活动：学生独立思考后小组讨论，难点是求以斜边为边长的正方形面积，可由师生共同总结得出可以通过割、补两种方法求出其面积，如图4，图5所示。教师在学生回答问题的基础上归纳方法-----割补法。可以求得C的面积为13，教师引导学生直接由正方形的面积等于边长的平方归纳出：直角三角形两条直角边的平方和等于斜边的平方。‎ 探究3：通过去网格我们得出了猜想：直角三角形两条直角边的平方和等于斜边的平方。即如果直角三角形的两直角边长为a,b.斜边长为c.那么:a2＋b2＝c2 。‎ 证明猜想：‎ ‎（1）教师提前拿出准备好的四个全等的直角三角形，抽两名学生拼出一个大正方形，用两种拼法。‎ 师生活动：老师讲拼出来的图形粘贴到黑板上，学生通过独立思考，用“割”或“补”的方法得出勾股定理的证明 本节课是本章的起始课，重视引言教学，从国际数学家大会的会徽说起，设置悬念，引入课题。‎ 从最特殊的等腰直角三角形入手，通过观察正方形面积关系得到三遍关系。‎ 网格中的直角三角形也是直角三角形一种特殊情况，为计算方便，通常将直角边长设定为整数，进一步体会面积割补法，为探究无网络背景下直角三角形三边关系打下基础，提供方法。‎ 通过拼图活动 3‎ 过程，教师板书证明过程。‎ ‎（2）教师重点介绍用“割”的方法拼出来的图形就是我国著名的”“赵爽弦图”，同时向同学们介绍我国古代数学的骄傲。‎ 三、巩固练习（见PPT）‎ 设置了4个不同层次的练习题 四、课堂小结 ‎1.勾股定理的内容是什么？它有什么作用？‎ ‎2.在探索勾股定理的过程中，你经历了怎样的过程？‎ 五、课后作业 必做题：教材第28页习题17.1第1、2、3题 选做题：通过查阅资料写出勾股定理的其他证明方法(一种即可)‎ 板书设计：以课堂生成为准 教学反思：‎ ‎，调动学生思维的积极性，为学生提供从事数学活动的机会，发展学生的形象思维；使学生对定理的理解更加深刻，体会数学中数形结合思想。通过对赵爽弦图介绍，了解我国古代数学家对勾股定理的发现及证明做出的贡献，增强民主自豪感。通过了解勾股定理的证明方法，增强学生学习数学的自信心。‎ 通过练习题的设计，让学生会应用勾股定理。同时通过第四个练习题的设计，让学生感受数学来源于生活，服务于生活。‎ 3‎