人教版八年级数学（下册）期末复习专题卷二（及答案） 13页

人教版八年级数学（下册）‎ 期末复习专题卷二 ‎1.若Rt△ABC中,∠C=90°且c=13,a=12,则b=(　　)‎ A.11‎ B.8‎ C.5‎ D.3‎ ‎2.顺次连接矩形ABCD各边的中点,所得四边形必定是(　　)‎ A.邻边不等的平行四边形 B.矩形 C.正方形 D.菱形 ‎3.如图1所示,菱形中,对角线AC,BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于(　　)‎ A.3.5‎ B.4‎ C.7‎ D.14‎ ‎　 图1‎ ‎4.如图2所示,在Rt△ABC中,∠ACB=90°,若AB=15 cm,则正方形ADEC和正方形BCFG的面积和为(　　)‎ ‎　 图2‎ A.150 cm2‎ B.200 cm2‎ C.225 cm2‎ D.无法计算 ‎5.我国北方某地温度突然下降,某市一小区为帮助老人和孩子安全度过这寒冷的冬季,特在小区建一取暖房,该取暖房的地面是一块长方形,经测量长为40 m,宽为20 m,现准备从对角各引一条通道,则每条通道的长都为(　　)‎ A.5 m B.10 m C.20 m D.30 m ‎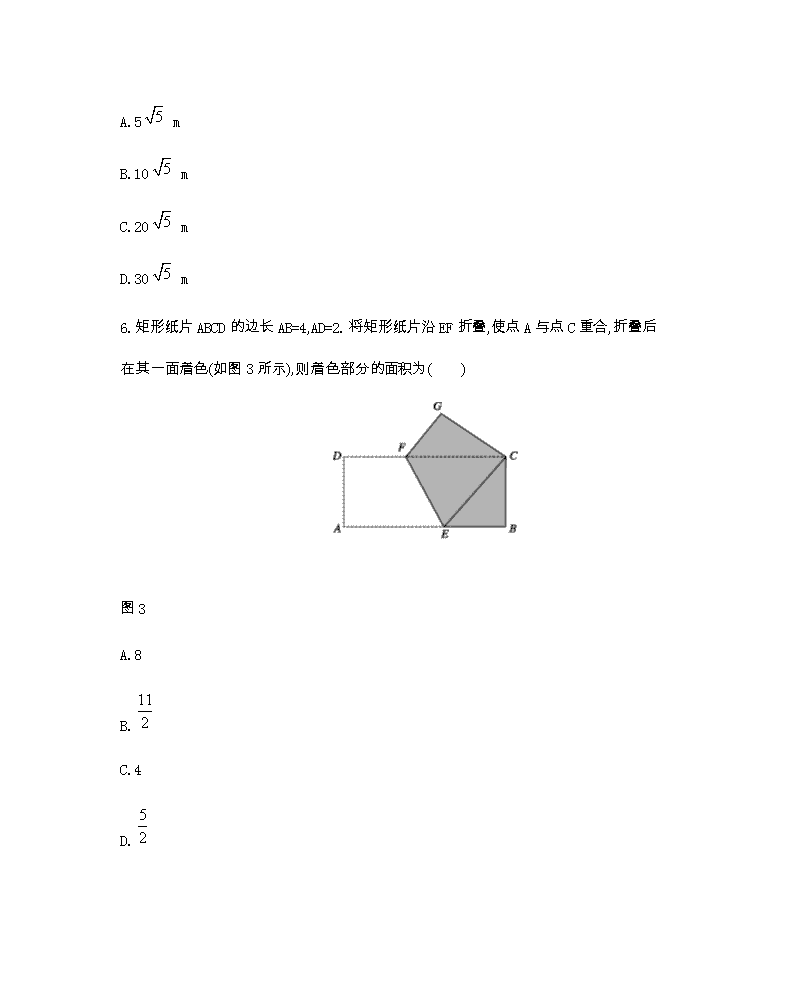6.矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图3所示),则着色部分的面积为(　　)‎ ‎ 图3‎ A.8‎ B.‎ C.4‎ D.‎ ‎7.如图4所示,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是(　　)‎ 图4‎ A.5‎ B.25‎ C.10+5‎ D.35‎ ‎8.如图5所示,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(　　)‎ ‎ 图5‎ A.6‎ B.12‎ C.20‎ D.24‎ ‎9.如图6所示,平行四边形ABCD中,AC,BD交于点O.若再增加一个条件　 　,就可得平行四边形ABCD为矩形.‎ 图6‎ ‎10.若菱形的周长为8,相邻两内角之比为3∶1,则菱形的高是  　.‎ ‎11.小明的爸爸要在高0.9 m,宽1.2 m的栅栏门的相对顶点间加一条加固木板,这条木板需　 　m长.‎ ‎12.如图7所示,在边长为1的正方形ABCD的外侧,作等边△ADE,则△ABE的面积为  　.‎ 图7‎ ‎13.如图8所示,在▱ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是　　　　. ‎ ‎ 图8‎ ‎14.图9中的螺旋形由一系列等腰直角三角形组成,其序号依次为①,②,③,④,⑤,…,则第n个等腰直角三角形的斜边长为  　.‎ ‎ 图9‎ ‎15.已知:如图10所示,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.‎ ‎　 图10‎ ‎16.如图11所示,在正方形ABCD中,E为AB中点,F为AD上一点,且AF=AD,试判断△FEC的形状,并说明理由.‎ ‎　 图11‎ ‎17.如图12所示,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.‎ ‎　 图12‎ ‎(1)求证:△ABE≌△ACE;‎ ‎(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.‎ ‎18.如图13所示,甲、乙两船同时从A港出发,甲船沿北偏东35°的方向,以每小时9海里的速度向B岛驶去,乙船沿南偏东55°的方向,以每小时12海里的速度向C岛驶去,3小时后两船同时到达了目的地.如果两船航行的速度不变且各自从B,C两岛出发相向而行,那么最少还需几小时才能相遇?‎ ‎　 图13‎ ‎19.如图14所示,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG,DE.‎ ‎(1)观察图形,猜想BG与DE之间的大小关系,并证明你的结论;‎ ‎(2)若延长BG交DE于点H,求证:BH⊥DE.‎ ‎　 图14‎ 参考答案 ‎1.C ‎2.D ‎3.A ‎4.C ‎5.C ‎6.B ‎7.B ‎8.D ‎9.∠BAD=90°(答案不唯一)‎ ‎10.‎ ‎11.1.5‎ ‎12. ‎ ‎13.1‎ ‎14.‎ ‎15. 证明:∵四边形ABCD是矩形,‎ ‎∴DC∥AB,DC=AB,‎ ‎∴CF∥AE.‎ ‎∵DF=BE,‎ ‎∴CF=AE,‎ ‎∴四边形AFCE是平行四边形,‎ ‎∴AF=CE.‎ ‎16. 解:△FEC是直角三角形.‎ 设正方形的边长为4a,则AE= BE=2a,‎ 所以AF=a,DF=3a,BC=CD=4a.‎ 由勾股定理,得FE2=5a2,EC2=20a2,CF2=25a2.‎ 所以FE2+EC2=FC2.‎ 所以△FEC是直角三角形.‎ ‎17.解:(1) 证明:∵AB=AC,点D为BC的中点,‎ ‎∴∠BAE=∠CAE,AE=AE,‎ ‎∴△ABE≌△ACE(SAS).‎ ‎(2) 当AE=2AD时,四边形ABEC是菱形.‎ 理由如下:∵AE=2AD,∴AD=DE,‎ 又点D为BC的中点,∴BD=CD,∴四边形ABEC为平行四边形.‎ ‎∵AB=AC,∴平行四边形ABEC为菱形.‎ ‎18. 解:∠BAC=180°-35°-55°=90°.‎ 由题意,知AB=9×3=27(海里),AC=12×3=36(海里).‎ 在Rt△ABC中,由勾股定理,‎ 得BC2=AB2+AC2=272+362=452.‎ ‎∴BC=45海里,‎ ‎∴BC÷(9+12)=45÷21=2(小时),‎ 即两船各自从B,C两岛出发相向而行,最少需2小时才能相遇.‎ ‎19.解:(1) 猜想:BG=DE;‎ ‎∵四边形ABCD与四边形CEFG都是正方形,‎ ‎∴BC=DC,∠BCG=∠DCE=90°,CG=CE,‎ ‎∴△BCG≌△DCE(SAS),‎ ‎∴BG=DE.‎ ‎(2) 证明:∵△BCG≌△DCE,‎ ‎∴∠CBG=∠CDE.‎ ‎∵∠BGD=∠CDE+∠DHG,‎ ‎∠BGD=∠CBG+∠BCG,‎ ‎∴∠DHG=∠BCG=90°,‎ ‎∴BH⊥DE.‎