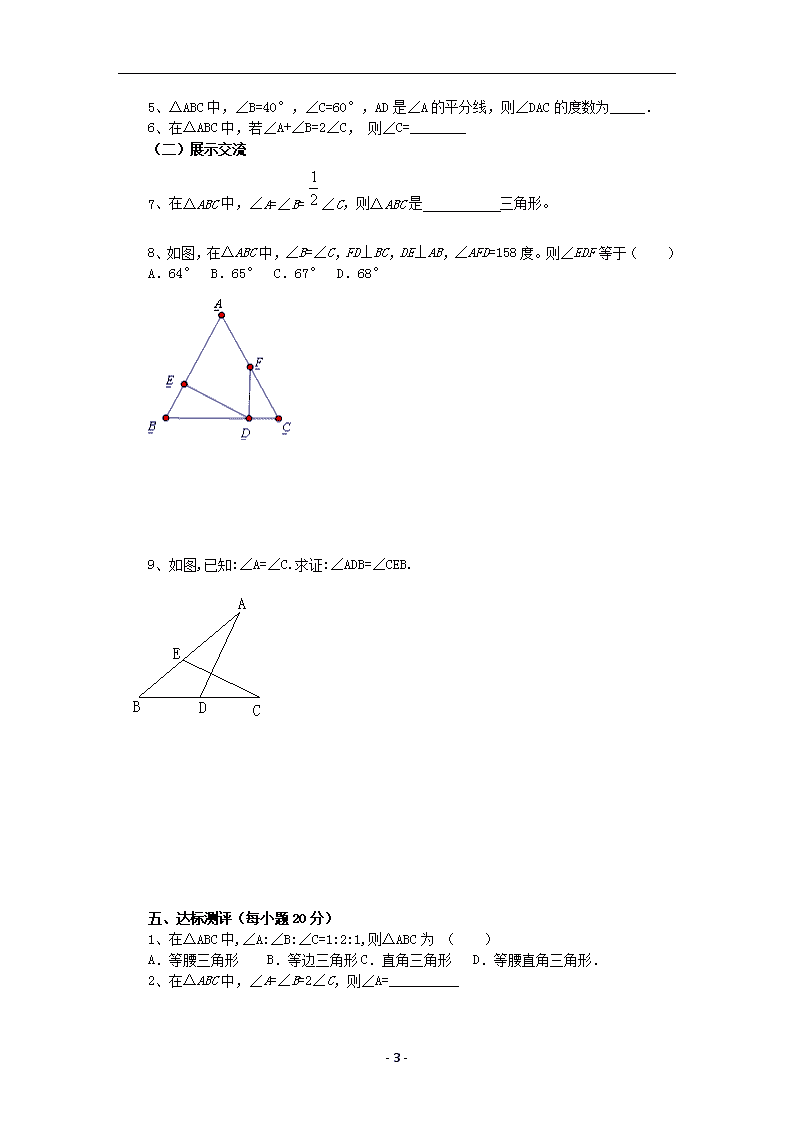- 61.01 KB
- 2021-10-26 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
- 1 -
5.5 三角形内角和定理
学习目标
知识目标:掌握三角形内角和定理的证明和它的简单应用。
能力目标:
1.经历利用剪拼三角形验证三角形内角和定理探索证明思路的过程;
2.初步领会辅助线在证明中的作用。
情感目标:培养学生思维的多样性。
学习重难点
学习重点:三角形内角和定理应用。
学习难点:三角形内角和定理应用;在证明过程中结合具体题型作出简便的辅助线。
自学交流:(通读课本 170 -171 页内容,思考以下几个问题)
1.三角形内角和定理的内容是什么?
2.什么叫辅助线?在画辅助线时有什么需要注意的问题?
3.三角形的一个外角与和它不相邻的两个外角有什么关系?
学习准备:
用纸片做两个三角形。
学习过程:
一、回顾与思考
(1)根据题意, ;
(2)根据题设、结论、结合图形,写出 ;
(3)经过分析,写出 。
二、新知探究
三、动手操作,合作发现
补充定理内容:三角形三个内角的和等于_______________
(一)运用剪拼的方法证明三角形内角和定理
(二)通过推理证明定理
剪拼的方法很简单,那么如何用推理的方法证明这一定理呢?
方法一:结合黑板上学生的展示提问以下两个问题:
1.根据剪拼证明定理,我们发现三角形的各内角做了怎样的移动?
2.如果不做剪拼,在图中你能否想到办法将三个角移到同一个顶点处?
3.根据所给的图,写出已知,求证,并给出证明。
分析:等于 180°的角有___;再有,平行状态下的______。
- 2 -
除了以上的方法,你还能对原三角形进行怎样的处理,从而也能证明三角形的内角和定
理呢?小组讨论完成。
方法二:
证明小结:
例 1 在△ABC 中,∠B=36°,∠C=62°,AD 是△ABC 的角平分线,求∠ADB 的度数。
四、学以致用
(一)基础巩固
1、△ABC 中可以有 3 个锐角吗? 3 个直角呢? 2 个直角呢?若有 1 个直角另外两角有
什么特点?三个内角都能小于 600 吗?
2、三角形的三个内角中,只能有____个直角或____个钝角.
3、任何一个三角形中,至少有____个锐角;至多有____个锐角.
4、若一个三角形三个内角度数的比为 1︰2︰3,那么这个三角形是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等边三角形
- 3 -
5、△ABC 中,∠B=40°,∠C=60°,AD 是∠A 的平分线,则∠DAC 的度数为_____.
6、在△ABC 中,若∠A+∠B=2∠C, 则∠C=________
(二)展示交流
7、在△ABC 中,∠A=∠B= 2
1
∠C,则△ABC 是 三角形。
8、如图,在△ABC 中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158 度。则∠EDF 等于( )
A.64° B.65° C.67° D.68°
9、如图,已知:∠A=∠C.求证:∠ADB=∠CEB.
�
E
�
D
�
C
�
B
�
A
五、达标测评(每小题 20 分)
1、在△ABC 中,∠A:∠B:∠C=1:2:1,则△ABC 为 ( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形.
2、在△ABC 中,∠A=∠B=2∠C,则∠A=__________
- 4 -
3、在△ABC 中,∠A=105°,∠B—∠C=15°,则∠C 的度数为________.
4、△ABC 中,∠C=90°,CD⊥AB,∠B=63°,则∠DCA=________.
5、如图,在△ABC 中,∠ABC=∠C,BD 是 AC 边上的高,∠ABD=20°,
求∠C 的度数。
六、总结归纳
相关文档
- 北师大版数学八年级上册 《课堂设2021-10-263页
- 八年级下册数学教案 1-3 第1课时 2021-10-262页
- 八年级上数学课件《勾股定理的逆定2021-10-2613页
- 人教版八年级上语文同步训练:昆明的2021-10-263页
- 2019-2020学年山东省济南市章丘区2021-10-267页
- 北师大版八年级下册数学同步练习课2021-10-2631页
- 2020学年度八年级物理上册长度和时2021-10-2616页
- 八年级上语文课件《苏州园林》 人2021-10-2633页
- 人教版八年级历史上册战略大决战2021-10-2628页
- 最新湘教版初中地理八年级下册《62021-10-2644页