《同步课时卷》北师版八年级数学（下册）6 6页

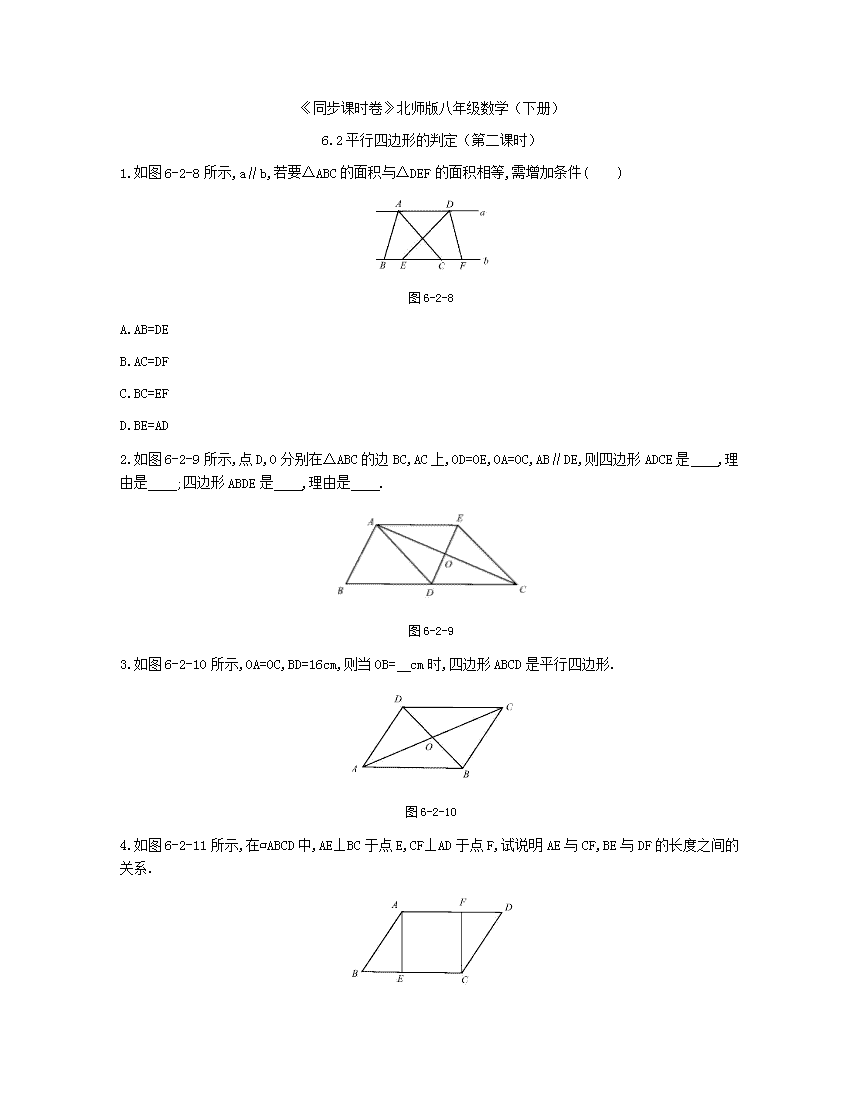
‎《同步课时卷》北师版八年级数学（下册）‎ ‎6.2平行四边形的判定（第二课时）‎ ‎1.如图6-2-8所示,a∥b,若要△ABC的面积与△DEF的面积相等,需增加条件(　　)‎ 图6-2-8‎ A.AB=DE B.AC=DF C.BC=EF D.BE=AD ‎2.如图6-2-9所示,点D,O分别在△ABC的边BC,AC上,OD=OE,OA=OC,AB∥DE,则四边形ADCE是　　,理由是　　;四边形ABDE是　　,理由是　　. ‎ 图6-2-9‎ ‎3.如图6-2-10所示,OA=OC,BD=16cm,则当OB=　cm时,四边形ABCD是平行四边形.‎ 图6-2-10‎ ‎4.如图6-2-11所示,在▱ABCD中,AE⊥BC于点E,CF⊥AD于点F,试说明AE与CF,BE与DF的长度之间的关系.‎ 图6-2-11‎ ‎5.下列命题中,真命题有(　　)‎ ‎①对角线互相平分的四边形是平行四边形;‎ ‎②两组对角分别相等的四边形是平行四边形;‎ ‎③一组对边平行,另一组对边相等的四边形是平行四边形.‎ A.3个 B.2个 C.1个 D.0个 ‎6.如图6-2-12所示,AF∥BG,AB∥CD,CE⊥BG,FG⊥BG,点E,G为垂足,则下列说法错误的是(　　)‎ 图6-2-12‎ A.AB=CD B.EC=FG C.点C到直线BG的距离就是线段CE的长 D.直线AF与直线BG的距离就是线段CD的长 ‎7.平面内与直线l距离为8cm的直线有　　条. 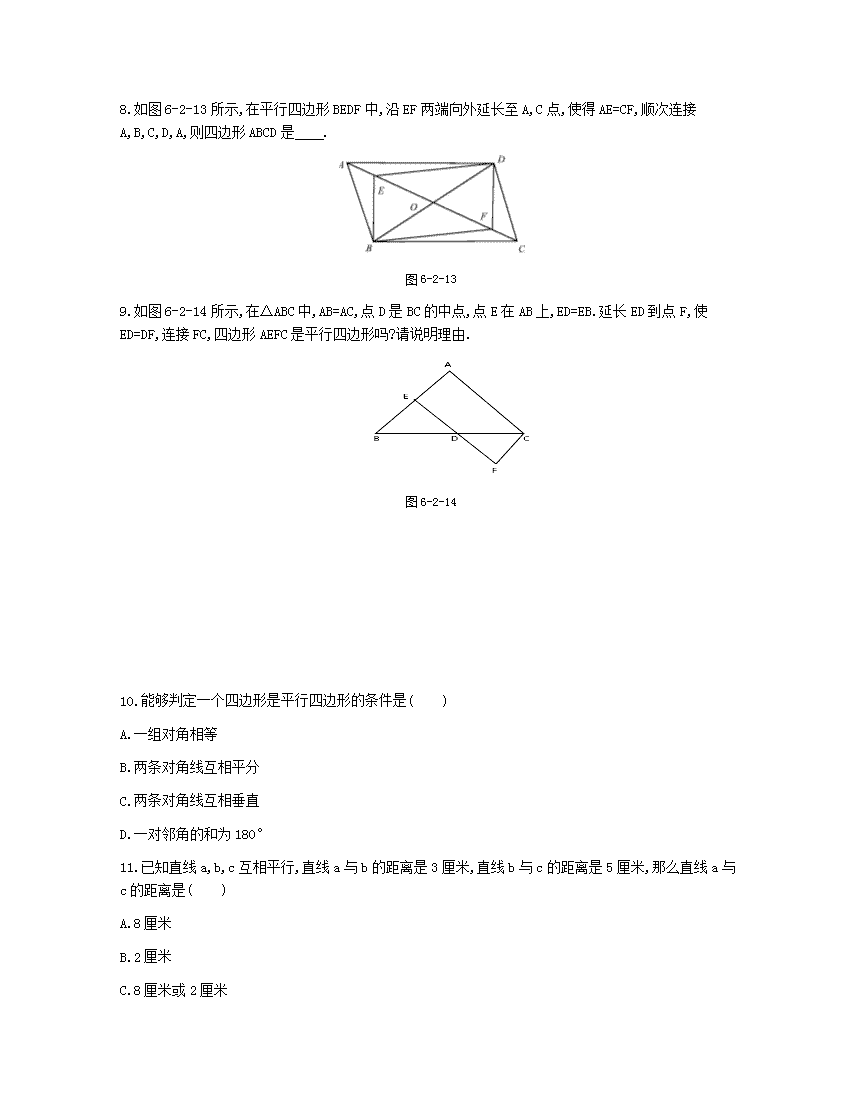‎ ‎8.如图6-2-13所示,在平行四边形BEDF中,沿EF两端向外延长至A,C点,使得AE=CF,顺次连接A,B,C,D,A,则四边形ABCD是　　. ‎ 图6-2-13‎ ‎9.如图6-2-14所示,在△ABC中,AB=AC,点D是BC的中点,点E在AB上,ED=EB.延长ED到点F,使ED=DF,连接FC,四边形AEFC是平行四边形吗?请说明理由.‎ 图6-2-14‎ ‎10.能够判定一个四边形是平行四边形的条件是(　　)‎ A.一组对角相等 B.两条对角线互相平分 C.两条对角线互相垂直 D.一对邻角的和为180°‎ ‎11.已知直线a,b,c互相平行,直线a与b的距离是3厘米,直线b与c的距离是5厘米,那么直线a与c的距离是(　　)‎ A.8厘米 B.2厘米 C.8厘米或2厘米 D.不能确定 ‎12.如图6-2-15,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(　　)‎ 图6-2-15‎ A.6‎ B.12‎ C.20‎ D.24‎ ‎13.如图6-2-16所示,已知直线m∥n,点A,B为直线n上两点,点C,D为直线m上两点,CB与AD相交于点O,请写出图中面积相等的各对三角形　　. ‎ 图6-2-16‎ ‎14.如图6-2-17所示,AB∥EF,且AB=EF,点C,D在BE上,BC=DE,AF与CD相交于点O.求证:AD∥CF.‎ 图6-2-17‎ 参考答案 ‎1.C ‎2.平行四边形对角线互相平分的四边形是平行四边形平行四边形两组对边分别平行的四边形是平行四边形 ‎3.8‎ ‎4.证明:∵四边形ABCD为平行四边形,‎ ‎∴∠B=∠D,AB=CD,‎ 又∵AE⊥BC,CF⊥AD,‎ ‎∴∠AEB=∠CFD=90°,‎ ‎∴△ABE≌△CDF,‎ ‎∴AE=CF,BE=DF.‎ ‎5.B ‎6.D ‎7.2‎ ‎8.平行四边形 ‎9.解:四边形AEFC是平行四边形.理由如下:‎ 连接BF,EC.‎ ‎∵AB=AC,‎ ‎∴∠ABC=∠ACB.‎ ‎∵ED=EB,‎ ‎∴∠ABC=∠EDB.‎ ‎∴∠ACB=∠EDB,‎ ‎∴EF∥AC.‎ ‎∵点D是BC的中点,‎ ‎∴BD=CD.‎ 又∵ED=DF,‎ ‎∴四边形BECF为平行四边形,‎ ‎∴BE∥CF,即AE∥CF.‎ ‎∴四边形AEFC是平行四边形.‎ ‎10.B ‎11.C ‎12.D ‎13.△ABC和△ABD,△AOC和△BOD,△ACD和△BDC ‎14.证明:连接AE,BF,AC,DF.‎ ‎∵AB∥EF,且AB=EF,‎ ‎∴四边形ABFE为平行四边形,‎ ‎∴AO=OF,EO=BO.‎ 又∵BC=DE,‎ ‎∴DO=CO,‎ ‎∴四边形ACFD为平行四边形,‎ ‎∴AD∥CF.‎