八年级下册数学教案19-2-3 一次函数与方程、不等式 人教版 3页

‎19.2.3 一次函数与方程、不等式 学习目标：‎ ‎1、理解一次函数与一元一次方程、一元一次不等式及二元一次方程（组）之间的关系.‎ ‎ 2、能用函数的观点解一元一次方程、一元一次不等式及二元一次方程（组）.‎ ‎3、熟练地掌握用数形结合法解一元一次方程、一元一次不等式及二元一次方程（组）.‎ 重点难点：‎ ‎1、一次函数与一元一次方程、一元一次不等式及二元一次方程（组）之间的关系. 2、用函数的观点解一元一次方程、一元一次不等式及二元一次方程（组）.‎ 学习过程 一、阅读课本[来源:Z&xx&k.Com]‎ 二、自学指导 ‎【活动1】‎ ‎①已知函数y＝2x＋20，当函数y＝0时，求得自变量x＝ .‎ ‎②解方程2x＋20＝0，求得x＝ .‎ ‎①②的联系是：在函数y＝2x＋20中，当y＝0时，该函数就变成了方程 ,所以解方程2x＋20＝0就相当于在 中，已知 ，求 的值.‎ ‎【活动2】‎ ‎①已知函数y＝2x－4，当函数y＞0时，求得自变量x的取值范围是 .‎ ‎②解不等式2x－4＞0,求得x .‎ ‎①②的联系是：在函数y＝2x－4中，当函数y＞0时，该函数就变成了不等式 ，所以解不等式2x－4＞0就相当于在 中，已知 ，求 的取值范围.‎ ‎【活动3】将下列二元一次方程转化成一次函数y＝kx＋b（k,b为常数，k≠0）的形式 ‎① 3x＋5y＝8 ；② 2x－y＝1 .‎ 归纳：任何一个二元一次方程都可转化成 的形式,所以任何一个二元一次方程的图象都是 .‎ ‎【活动4】‎ 解二元一次方程组得 ，所以直线3x＋5y＝8与直线2x－y＝1的交点 坐标为 .‎ 三、知识归纳 ‎1、解方程ax＋b＝0（a,b为常数，a≠0）等同于在一次函数y＝ax＋b（a,b为常数，a≠0）‎ 中 已知 ，求 .‎ ‎2、从“数”的角度看：一元一次不等式kx+b>0（或kx+b<0）的解，就是一次函数 的函数值 （或 ）时，相应的自变量x的取值范围。　‎ ‎3、从“形”角度看：一元一次不等式kx+b>0（或kx+b<0）的解，就是一次函数 的图像在x轴 （或 ）时，相应的自变量x的取值范围。　‎ ‎4、一般地，每个二元一次方程组都对应两个 ，于是也对应两条 .从“数”的角度看，解方程组相当于考虑 ，以及这个函数值是何值；从“形”的角度看，解方程组相当于确定 .即 二元一次方程组的解 两直线交点坐标 ‎5、‎ ‎6、图示理解 两个二元一次方程组成的方程组都对应两个一次函数，于是也对应两条直线。‎ ‎ ‎ 四、 课堂练习 ‎1、在一次函数y＝x－9中，要得到y＝－2，则x应取（ ）‎ A.－7 B.7 C.11 D.－11‎ ‎2、若一次函数y＝kx＋b图象与x轴相交点（3，0），则kx＋b＝0的解为（ ）‎ x y o p ‎·‎ y＝ax＋b y＝kx－c ‎-1‎ ‎-3‎ A.x＝－3 B. x＝3 C. x＝0 D. 不能确定 ‎3、如图，函数y＝ax＋b与y＝kx－c的图象相交于点P，则根据图象 可得二元一次方程组 的解是 .‎ ‎4、如右图所示：是一次函数y＝－的图象，那么不等式 ‎－≤8的解集是（ ）[来源:学.科.网Z.X.X.K]‎ A.x＜ 10 B. x≥ 10 C. x≤ 10 D. 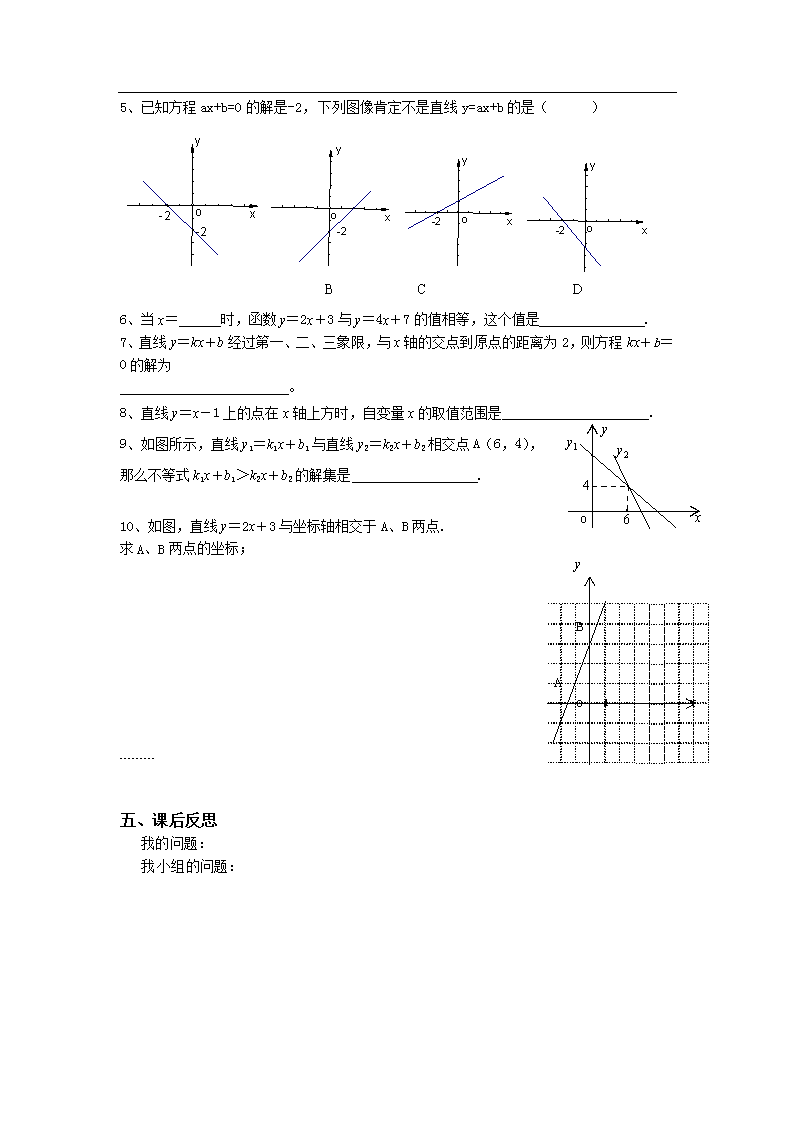x≤13‎ ‎5、已知方程ax+b=0的解是-2，下列图像肯定不是直线y=ax+b的是（ ） [来源:Z|xx|k.Com]‎ D C ‎ B ‎ ‎6、当x＝ 时，函数y＝2x＋3与y＝4x＋7的值相等，这个值是 .‎ ‎7、直线y＝kx＋b经过第一、二、三象限，与x轴的交点到原点的距离为2，则方程kx＋b＝0的解为 ‎ 。‎ x y o ‎·‎ y1‎ y2‎ ‎6‎ ‎4‎ ‎·‎ ‎·‎ ‎8、直线y＝x－1上的点在x轴上方时，自变量x的取值范围是 .‎ ‎9、如图所示，直线y1＝k1x＋b1与直线y2＝k2x＋b2相交点A（6，4），‎ 那么不等式k1x＋b1＞k2x＋b2的解集是 .‎ ‎[来源:学。科。网Z。X。X。K]‎ ‎10、如图，直线y＝2x＋3与坐标轴相交于A、B两点.‎ x y o ‎1‎ B A 求A、B两点的坐标；‎ ‎[来源:学。科。网Z。X。X。K]‎ 五、课后反思 我的问题：‎ 我小组的问题：‎