【精品试题】人教版 八年级下册数学 第十九章 一次函数周周测9（全章）（含答案） 7页

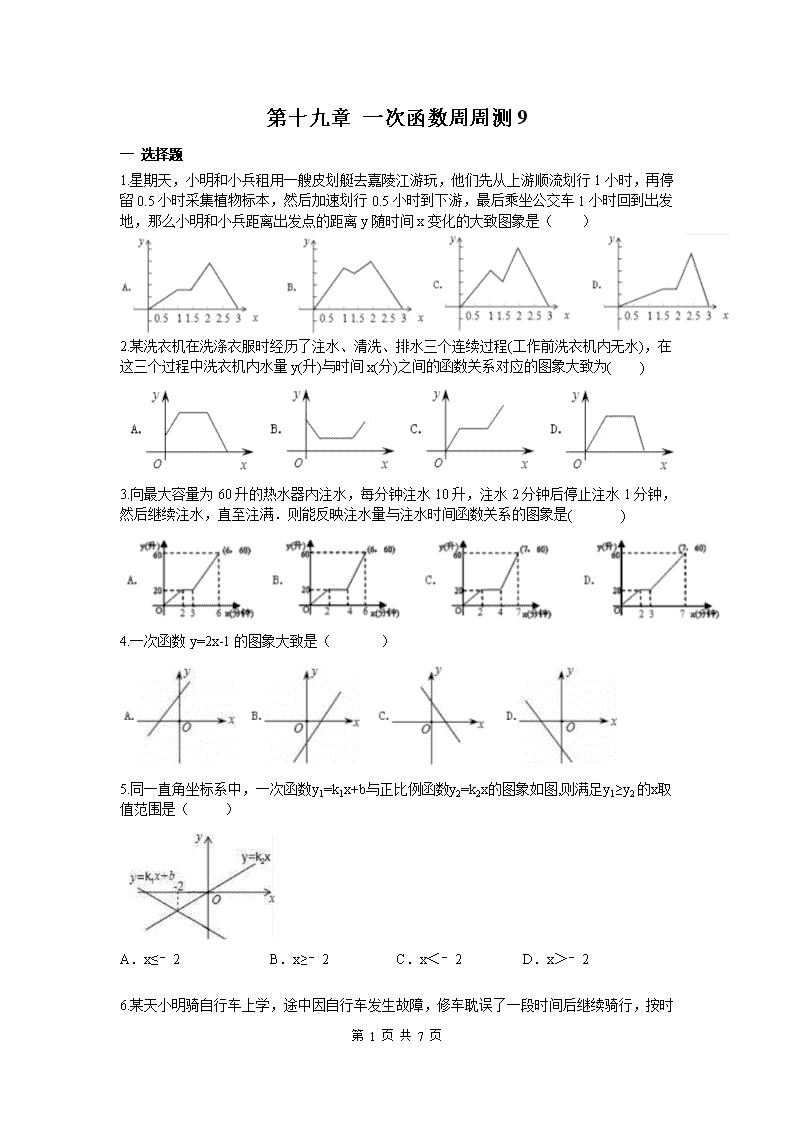
第 1 页 共 7 页 第十九章 一次函数周周测 9 一 选择题 1.星期天，小明和小兵租用一艘皮划艇去嘉陵江游玩，他们先从上游顺流划行 1小时，再停 留 0.5小时采集植物标本，然后加速划行 0.5小时到下游，最后乘坐公交车 1小时回到出发 地，那么小明和小兵距离出发点的距离 y随时间 x变化的大致图象是（ ） 2.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水)，在 这三个过程中洗衣机内水量 y(升)与时间 x(分)之间的函数关系对应的图象大致为( ) 3.向最大容量为 60升的热水器内注水，每分钟注水 10升，注水 2分钟后停止注水 1分钟， 然后继续注水，直至注满．则能反映注水量与注水时间函数关系的图象是( ) 4.一次函数 y=2x-1的图象大致是（ ） 5.同一直角坐标系中，一次函数y1=k1x+b与正比例函数y2=k2x的图象如图,则满足y1≥y2的x取 值范围是（ ） A．x≤﹣2 B．x≥﹣2 C．x＜﹣2 D．x＞﹣2 6.某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时 第 2 页 共 7 页 赶到了学校. 图描述了他上学的情景，下列说法中错误的是( ) A．修车时间为 15分钟 B．学校离家的距离为 2000米 C．到达学校时共用时间 20分钟 D．自行车发生故障时离家距离为 1000米 7.若一次函数 y=ax＋b的图象经过第一、二、四象限，则下列不等式中总是成立的是( ) A．ab＞0 B．a－b＞0 C．a2＋b＞0 D．a＋b＞0 8.在平面直角坐标系中，若直线 y=kx＋b经过第一、三、四象限，则直线 y=bx＋k不经过．．．的 象限是( ) A．第一象限 B．第二象限 C．第三象限 D．第四象限 9.已知一次函数 y=-0.5x+2，当 1≤x≤4时，y的最大值是（ ）． A．2 B．1.5 C．2.5 D．-6 10.在市举办的“划龙舟，庆端午”比赛中，甲、乙两队在比赛时的路程 s（米）与时间 t（分 钟）之间的函数关系图象如图所示，根据图象得到下列结论，其中错误的是（ ） A．这次比赛的全程是 500米 B．乙队先到达终点 C．比赛中两队从出发到 1.1分钟时间段，乙队的速度比甲队的速度快 D．乙与甲相遇时乙的速度是 375米/分钟 11.如图,在平面直角坐标系中,△ABC 的顶点坐标分别为 A(1,1),B(3,1),C(2,2)当直线 y=0.5x+b与△ABC有交点时,b的取值范围是( ) A．-1≤b≤1 B．-1≤b≤0.5 C．-0.5≤b≤0.5 D．-0.5≤b≤1 12.如图，在平面直角坐标系中，直线 y=-3x+3 与坐标轴分别交于 A，B两点，以线 段 AB为边，在第一象限内作正方形 ABCD，将正方形 ABCD沿 x轴负方向平移 a个单位 长度，使点 D恰好落在直线 y=3x-2上，则 a的值为（ ） A．1 B．2 C．﹣1 D．﹣1.5 二 填空题 13.3x﹣y=7中，变量是 ，常量是 ．把它写成用 x的式子表示 y的形式 第 3 页 共 7 页 是 ． 14.已知 y-2与 x成正比,且当 x=1时, y=-6，则 y与 x的关系式是____________。 15.若直线 y=kx+b（k≠0）的图象经过点（0，2），且与坐标轴所围成的三角形面积是 2，则 k的值为 16.一次函数 y=（m+2）x+1，若 y随 x的增大而增大，则 m的取值范围是 ． 17.已知点 P既在直线 y=﹣3x﹣2上，又在直线 y=2x+8 上，则 P点的坐标为 ． 18.如图，直线 与x轴、y轴分别交于点A和B，M是OB上的一点，若将 ABM 沿AM折叠，点B恰好落在x轴上的点 处， 则直线AM的解析式为 . 三 解答题 19.已知把直线 y=kx+b（k≠0）沿着 y轴向上平移 3个单位后，得到直线 y=﹣2x+5． （1）求直线 y=kx+b（k≠0）的解析式； （2）求直线 y=kx+b（k≠0）与坐标轴围成的三角形的周长． 20.为表彰学习进步的同学，某班生活委员到文具店买文具作为奖品．如果买 4个笔记本和 2 支钢笔，则需 86元；如果买 3个笔记本和 1支钢笔，则需 57元． （1）求每个笔记本和每支钢笔的售价． （2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过 10支，那么超出部分可以 享受八折优惠，若买 x(x>0)支钢笔需要花 y元，求 y与 x的函数关系式． 第 4 页 共 7 页 21.我校为开展研究性学习，准备购买一定数量的两人学习桌和三人学习桌，若购买 1张两 人学习桌，1张三人学习桌需 230元；若购买 2张两人学习桌，3张三人学习桌需 590元． （1）求两人学习桌和三人学习桌的单价； （2）学校欲投入资金不超过 6600元，购买两种学习桌共 60张，以至少满足 137名学生的 需求，有几种购买方案？并求哪种购买方案费用最低？ 22.为了贯彻落实市委市政府提出的“精准扶贫”精神．某校特制定了一系列关于帮扶A，B两 贫困村的计划．现决定从某地运送 152箱鱼苗到A，B两村养殖.若用大、小货车共 15辆， 则恰好能一次性运完这批鱼苗，已知这两种大、小货车的载货能力分别为 12箱/辆和 8箱/ 辆，其运往A．B两村的运费如下表： 目的地车型 A村(元/辆) B村(元/辆) 大货车 800 900 小货车 400 600 (1)这 15辆车中大、小货车各多少辆？ (2)现安排其中 10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A．B 两村总费用为y元，试求出y与x的函数表达式； (3)在(2)的条件下，若运往A村的鱼苗不少于 100箱，请你写出使总费用最少的货车调配方案， 并求出最少费用． 23.如图，在平面直角坐标系中，一次函数 y=kx+b的图象与 x轴交于点 A（-3，0），与 y 轴交于点 B，且与正比例函数 的图象交点为 C（m，4）．求： （1）一次函数 y=kx+b 的解析式； （2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，则点D的坐标为 ； 第 5 页 共 7 页 （3）在 x 轴上求一点 P 使△POC 为等腰三角形，请求出所有符合条件的点 P 的坐标． 第十九章 一次函数周周测 9 试题答案 1.A 2.D .3.D 4.B 5.A 6.A 7.C 8.C 9.B 10.C 11.D 12.A 13.x和 y；3和 7；y=3x﹣7． 14.y=-8x+2 15.±1 16.m＞﹣2 17.（-2,4） 18.y=-0.5x+3 19.解：（1）直线 y=kx+b（k≠0）沿着 y 轴向上平移 3 个单位后，得到直线 y=-2x+5， 可得直线 y=kx+b 的解析式为 y=-2x+5-3=-2x+2. （2）在直线 y=-2x+2 中，当 x=0，则 y=2，当 y=0，则 x=1，∴直线 l 与两条坐标轴围成 的三角形的周长为 20. 第 6 页 共 7 页 21.解：（1）设两人桌每张 x元，三人桌每张 y元， 根据题意得， 解得 x=100,y=130. （2）设两人桌 m张，则三人桌（60﹣m）张，根据题意可得 ，解 得 40≤m≤43.∵m为正整数，∴m为 40、41、42、43， 共有 4种方案，设费用为W, W=100m+130（60﹣m）=﹣30m+7800，m=43 时，W最小为 6510元． 22. 解：（1）设大货车用 x 辆，小货车用 y 辆，根据题意得 答：大货车用 8 辆，小货车用 7 辆． （2）y=800x+900（8-x）+400（10-x）+600[7-（10-x）]=100x+9400．（3≤x≤8， 且 x 为整数）． （3）由题意得 12x+8（10-x）≥100，解得 x≥5，又∵3≤x≤8，∴5≤x≤8 且为整数.∵ y=100x+9400，k=100＞0，y 随 x 的增大而增大，∴当 x=5 时，y 最小，最小值为 y=100 ×5+9400=9900（元）． 答：使总运费最少的调配方案是：5 辆大货车、5 辆小货车前往 A 村；3 辆大货车、2 辆小 货车前往 B 村，最少运费为 9900 元． 23.解：（1）∵点 C 在正比例函数图象上， ＝4，m=3.∵点 C（3，4）、A（-3，0） 在一次函数图象上，∴代入一次函数解析式可得 解得 ∴一次函数的解 析式为 . （2）（-2，5）或（-5，3） 解析：如图，过点 D1 作 D1E⊥y 轴于点 E，过点 D2 作 D2F ⊥x 轴于点 F，∵点 D 在第二象限，△DAB 是以 AB 为直角边的等腰直角三角形，∴AB=BD2. 第 7 页 共 7 页 ∵∠D1BE+∠ABO=90°，∠ABO+∠BAO=90°，∴∠BAO=∠EBD1. ∵在△BED1 和△AOB 中， ∴△BED1≌△AOB（AAS），∴BE=AO=3， D1E=BO=2，即可得出点 D 的坐标为（-2，5）.同理可得出：△AFD2≌△AOB，∴FA=BO=2， D2F=AO=3，∴点 D 的坐标为（-5，3）．综上可知点 D 的坐标为（-2，5）或（-5，3）． （3）当 OC 是腰，O 是顶角的顶点时，OP=OC，则 P 的坐标为（5，0）或（-5，0）； 当 OC 是腰，C 是顶角的顶点时，CP=CP，则 P 与 O 关于 x=3 对称，则 P 的坐标是（6， 0）；当 OC 是底边时，设 P 的坐标为（a，0），则（a-3）2+42=a2，解得 a= ，此时 P 的坐标是（ ，0）；综上可知 P 的坐标为（5，0）或（-5，0）或（6，0）或（ ， 0）．