- 79.04 KB
- 2021-10-27 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
- 1 -
13.3 等腰三角形
第 3 课时
教学目的
1、使学生熟练地运用等腰三角形的性质求等腰三角形内角的角度。
2、熟识等边三角形的性质及判定.
3、通过例题教学,帮助学生总结代数法求几何角度,线段长度的方法。
教学重点:
等腰三角形的性质及其应用。
教学难点:
简洁的逻辑推理。
教学过程
一、复习巩固
1.叙述等腰三角形的性质,它是怎么得到的?
等腰三角形的两个底角相等,也可以简称“等边对等角”。把等腰三角形对折,折叠两
部分是互相重合的,即 AB 与 AC 重合,点 B 与点 C 重合,线段 BD 与 CD 也重合,所以
∠B=∠C。
等腰三角形的顶角平分线,底边上的中线和底边上的高线互相重合,简称“三线合一”。
由于 AD 为等腰三角形的对称轴,所以 BD= CD,AD 为底边上的中线;∠BAD=∠CAD,
AD 为顶角平分线,∠ADB=∠ADC=90°,AD 又为底边上的高,因此“三线合一”。
2.若等腰三角形的两边长为 3 和 4,则其周长为多少?
二、新课
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。
我们把三条边都相等的三角形叫做等边三角形。
等边三角形具有什么性质呢?
1.请同学们画一个等边三角形,用量角器量出各个内角的度数,并提出猜想。
2.你能否用已知的知识,通过推理得到你的猜想是正确的?
等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到∠A=∠B=C
又由∠A+∠B+∠C=180°,从而推出∠A=∠B=∠C=60°。
3.上面的条件和结论如何叙述?
等边三角形的各角都相等,并且每一个角都等于 60°。
等边三角形是轴对称图形吗?如果是,有几条对称轴?
等边三角形也称为正三角形。
例 1.在△ABC 中,AB=AC,D 是 BC 边上的中点,∠B=30°,求∠1 和∠ADC 的
度数。
分析:由 AB=AC,D 为 BC 的中点,可知 AB 为 BC 底边上的中线,由“三线合一”
可知 AD 是△ABC 的顶角平分线,底边上的高,从而∠ADC=90°,∠l=∠BAC,由于∠
C=∠B=30°,∠BAC 可求,所以∠1 可求。
问题 1:本题若将 D 是 BC 边上的中点这一条件改为 AD 为等腰三角形顶角平分线或底
- 2 -
边 BC 上的高线,其它条件不变,计算的结果是否一样?
问题 2:求∠1 是否还有其它方法?
三、练习巩固
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合( )
b.有一个角是 60°的等腰三角形,其它两个内角也为 60°( )
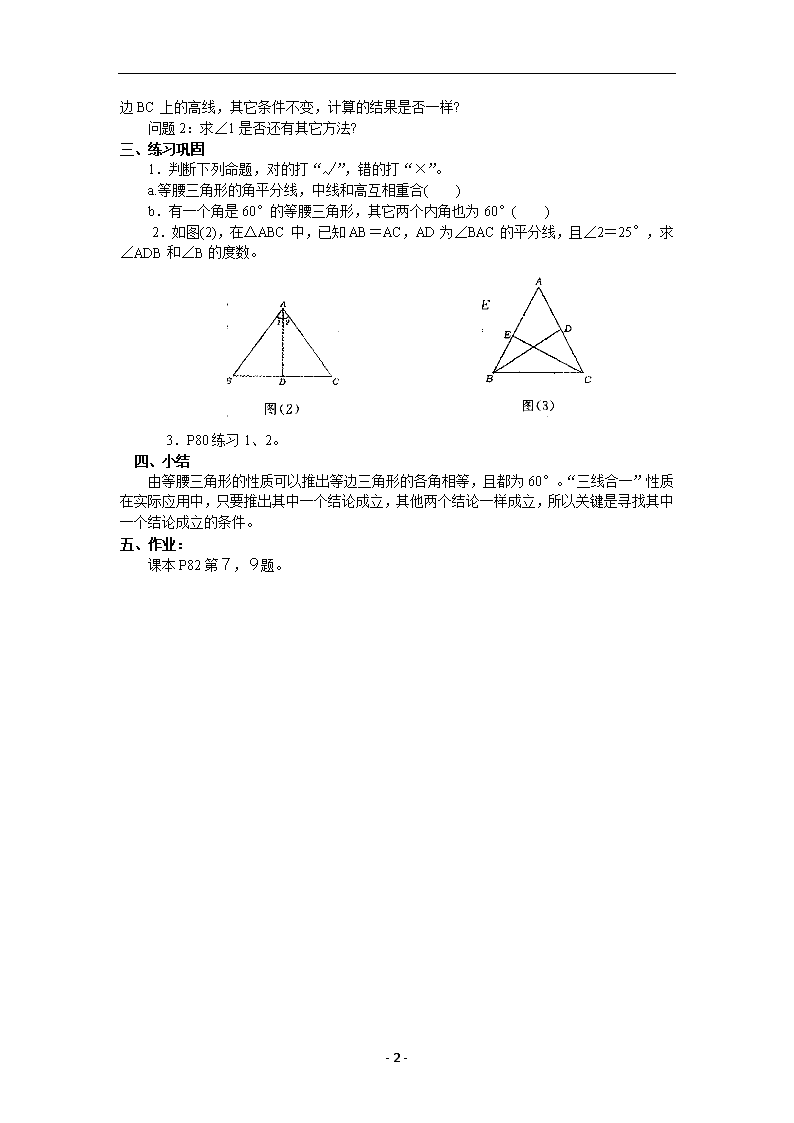
2.如图(2),在△ABC 中,已知 AB=AC,AD 为∠BAC 的平分线,且∠2=25°,求
∠ADB 和∠B 的度数。
3.P80 练习 1、2。
四、小结
由等腰三角形的性质可以推出等边三角形的各角相等,且都为 60°。“三线合一”性质
在实际应用中,只要推出其中一个结论成立,其他两个结论一样成立,所以关键是寻找其中
一个结论成立的条件。
五、作业:
课本 P82 第7,9题。