2020春八年级数学下册第20章平行四边形的判定20-1平行四边形的判定习题课件华东师大版 34页

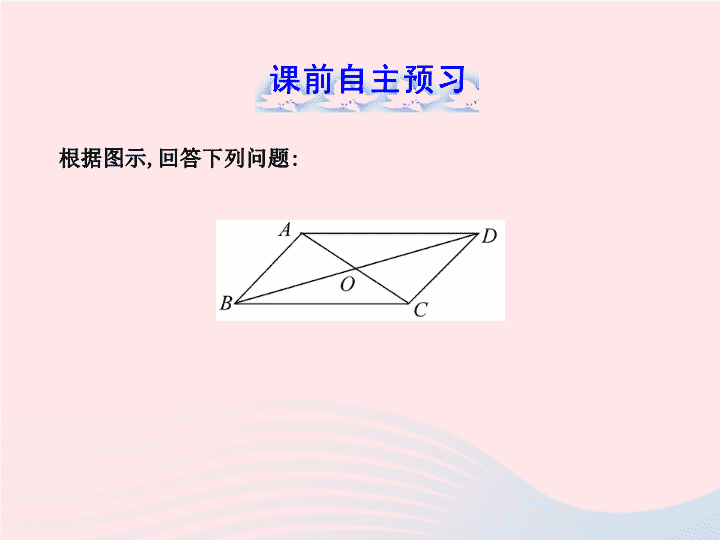
§20.1 平行四边形的判定 根据图示 , 回答下列问题 : (1) 两组 _____ 分别 _____ 的四边形是平行四边形； ∵ AB=___,AD=___, ∴ 四边形 ABCD 是平行四边形 . 对边 相等 CD BC 【 点拨 】 平行四边形的定义 : 两组对边分别平行的四边形是平行四边形，也可作为平行四边形的判定方法 . (2) 一组对边 _____ 且 _____ 的四边形是平行四边形； ∵ AB∥___,AB=___, ∴ 四边形 ABCD 是平行四边形 . (3) 对角线 _________ 的四边形是平行四边形； ∵ AO=___,BO=___, ∴ 四边形 ABCD 是平行四边形 . 平行 相等 CD CD 互相平分 CO DO (4) 两组 _____ 分别 _____ 的四边形是平行四边形； ∵∠ ABC=______,∠BAD=______, ∴ 四边形 ABCD 是平行四边形 . 对角 相等 ∠ADC ∠BCD 【 归纳 】 平行四边形的判定可以从对边、对角、对角线三个角度来分析 . 【 预习思考 】 一组对角相等的四边形是平行四边形吗？ 提示： 不是 . 平行四边形的判定 【 例 1】 已知， E ， F 是四边形 ABCD 的对角线 AC 上的两点， AE=CF ， BE=DF ， BE∥DF. 求证：四边形 ABCD 是平行四边形 . 【 解题探究 】 若证四边形 ABCD 是平行四边形，根据题中的条件，可以证明 AB CD , 需证△ ABE≌ △CDF ，从而得出 AB=CD ,∠BAE=∠DCF, 进而得出 AB∥CD,∵ 已知 AE=CF , BE=DF ,∴ 需证 ∠ AEB = ∠CFD , ∵BE∥DF,∴∠BEF=∠DFE,∴∠AEB=∠CFD, 问题得证 . 【 互动探究 】 在判定一个四边形是平行四边形时，若已知一组对边平行， 则还需证明什么条件？ 提示： 证明这一组对边相等或另一组对边平行 . 【 规律总结 】 平行四边形的判定口诀 要证平行四边形，两个条件才能行，一证对边都相等，或证对边都平行，一组对边也可以，必须相等且平行。对角线，是个宝，互相平分 “ 跑不了 ” ，对角相等也有用， “ 两组对角 ” 才能成 . 【 跟踪训练 】 1. 四边形 ABCD 中， AD∥BC ，要使四边形 ABCD 为平行四边形， 需要增加条件 _______( 只需填上一个你认为正确的即可 ). 【 解析 】 由 AD∥BC ，可以添加条件 AD=BC 或 AB∥CD 或∠ A=∠C 可以使四边形 ABCD 为平行四边形 . 答案： AD=BC( 或 AB∥CD 或∠ A=∠C) 2.(2012· 朝阳中考 ) 如图 , 在四边形 ABCD 中 ,E 是 BC 边的中点 , 连接 DE 并延长 , 交 AB 的延长线于 F 点 ,AB=BF, 请你添加一个条件 ( 不需要添加任何线段或字母 ), 使之能推出四边形 ABCD 为平行四边形 , 请证明 . 你添加的条件是 ______. 【 解析 】 添加的条件是 :CD∥AB( 除此条件外 , 其他条件能证明 四边形 ABCD 为平行四边形的均可 ) 证明 :∵CD∥AB,∴∠CDE=∠BFE. 又∵ EC=BE,∠DEC=∠FEB,∴△CED≌△BEF, ∴CD=BF. 又∵ AB=BF,∴AB=CD, ∴ 四边形 ABCD 是平行四边形 . 答案： CD∥AB( 答案不唯一 ) 3. 如图， E,F 是平行四边形 ABCD 的对角 线 AC 上的点， CE=AF. 请你猜想： BE 与 DF 有怎样的位置关系和数量关系？并 对你的猜想加以证明 . 【 解析 】 BE∥DF 且 BE=DF. 连结 BD ，交 AC 于点 O ，连结 DE ， BF. ∵ 四边形 ABCD 是平行四边形 ,∴BO=OD,AO=CO. 又∵ AF=CE, ∴AE=CF,∴EO=FO, ∴ 四边形 BEDF 是平行四边形 , ∴BE∥DF 且 BE=DF. 平行四边形的判定的应用 【 例 2】(6 分 ) 李大伯家有一口如图所示 的四边形的池塘，在它的四个角上均有 一棵大柳树，李大伯开挖池塘，使池塘 面积扩大一倍，又想保持柳树不动，如果要求新池塘成平行四边形的形状 . 请问李大伯的愿望能否实现 ? 若能，请画出你的设计图，并说明理由；若不能，请说明理由 . 【 规范解答 】 能， …………………………………………… 1 分 理由如下 : 连结 AC 和 BD 交于点 O ， 过点 A 和点 C 分别作 BD 的平行线， 过点 B 和点 D 分别作 AC 的平行线， 则四边形 EFGH 即是要求的图形 . 如图： …………………… 3 分 理由：∵ EF∥AC∥HG,EH∥BD∥FG, ∴ 四边形 AEBO, 四边形 BFCO, 四边形 DOCG, 四边形 AODH 是 平行四边形 ； ………………………………… 4 分 根据平行四边形的性质，得 S △AEB = S △AOB ,S △AHD = S △AOD ,S △FBC = S △OBC , S △CGD = S △COD . ……… 5 分 ∴四边形 EFGH 的面积为四边形 ABCD 的面积的两倍 . ……… 6 分 【 规律总结 】 平行四边形判定的应用解题时的两个步骤 (1) 判定一个四边形是平行四边形 . (2) 利用平行四边形的性质解决有关问题 . 【 跟踪训练 】 4. 工人师傅现在需要把一块三角形的铁板 ( 如图 ) ， 通过切割焊接成一个与其面积相等的平行四边形， 你能帮助他设计一种可行的方案吗 ? 请在图中画出 焊接线，并说明你的理由 . 【 解析 】 设计的方案如图所示，可分别取 AB, AC 边的中点 D,E ，连结 DE ，过点 C 作 CF∥AB ， 交 DE 的延长线于 F ，把△ ABC 沿 DE 切割后， 补在△ CFE 的位置上，就可焊接成 □ BCFD. 理由如下： ∵ E 是 AC 的中点，∴ AE=CE. ∵CF∥AB ，∴∠ ADF ＝∠ F. 又∵∠ AED ＝∠ CEF ，∴△ ADE≌△CFE, ∴AD=CF.∵D 是 AB 的中点 , ∴AD=BD ，故 BD=CF ，又∵ CF∥AB ，∴四边形 BCFD 是平行四边形 . 5. 小明的爸爸在钉制平行四边形框架时采用了下面的方法 . 将两根同样长的木条 AB ， CD 平行放置，再用木条 AD ， BC 加固，得到的四边形 ABCD 就是平行四边形，小明的爸爸这样做行吗？说明理由 . 【 解析 】 小明的爸爸这样做行，理由如下： 由题意知： AB∥CD,AB=CD, ∴ 四边形 ABCD 是平行四边形 . 1. 以不在同一直线上的三点为顶点作平行四边形，最多能 作 ( ) (A)4 个 (B)3 个 (C)2 个 (D)1 个 【 解析 】 选 B. 假设三点为 A ， B ， C, 分别以 AB,AC,BC 为对角 线，可以作出三个平行四边形 , 分别为 □ ACBD 1 、 □ ABCD 2 和 □ ABD 3 C ，如图 2. 如图，在 □ ABCD 中，对角线 AC ， BD 相交于 O ， E ， F 是对角线 AC 上的 两点，当 E ， F 满足下列哪个条件 时，四边形 DEBF 不一定是平行四 边形 ( ) (A)AE=CF (B)DE=BF (C)∠ADE=∠CBF (D)∠AED=∠CFB 【 解析 】 选 B.A 中能得到 OE=OF ，由 OB=OD 从而证明其为平行四边形； C 中能证明△ ADE≌△CBF ，得 AE=CF ，同 A 一样； D 中也能证明△ ADE≌△CBF. 3. 把两个全等的非等腰三角形拼成平行四边形，可拼成的不同平行四边形的个数为 ______ 个 . 【 解析 】 两个全等的三角形拼在一起，必须把相等的边重合，故有三种拼法，而每种拼法中有两种情况，一种拼成平行四边形，另一种不是平行四边形 ( 是一个轴对称图形 ) ，故可拼成三个不同的平行四边形 . 答案： 3 4. 如图所示，在 □ ABCD 中， E,F 分别是对 角线 BD 上的两点，且 BE=DF ，要证明四边 形 AECF 是平行四边形，最简单的方法是 根据 _____ 来证明 . 【 解析 】 连结 AC 交 BD 于点 O ，则 OA=OC,OB=OD ，又 BE=DF ，∴ OE=OF, ∴ 四边形 AECF 为平行四边形，故用两条对角线互相平分的四 边形是平行四边形来证明较简单 . 答案： 两条对角线互相平分的四边形是平行四边形 5.(2012· 徐州中考 ) 如图 ,C 为 AB 的中点 , 四边形 ACDE 为平行四边形 ,BE 与 CD 相交于点 F, 求证 :EF=BF. 【 证明 】 连结 EC,DB, 在 □ ACDE 中 ,AC DE, 又 C 是 AB 的中点， 即 AC=BC, ∴DE BC, ∴ 四边形 BDEC 是平行四边形 ,∴EF=BF.