人教版八年级数学上册专题训练(五)PPT 21页

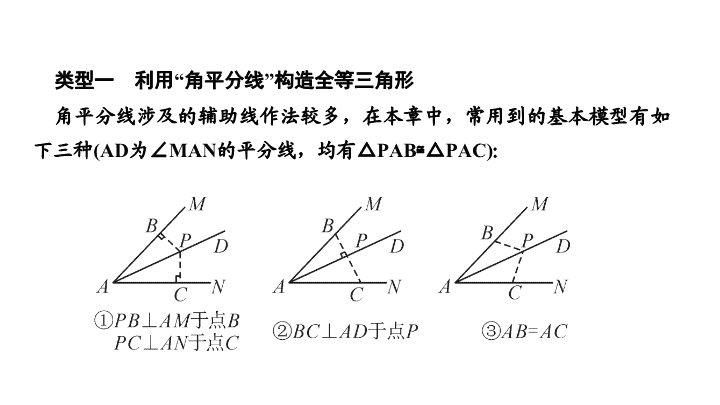
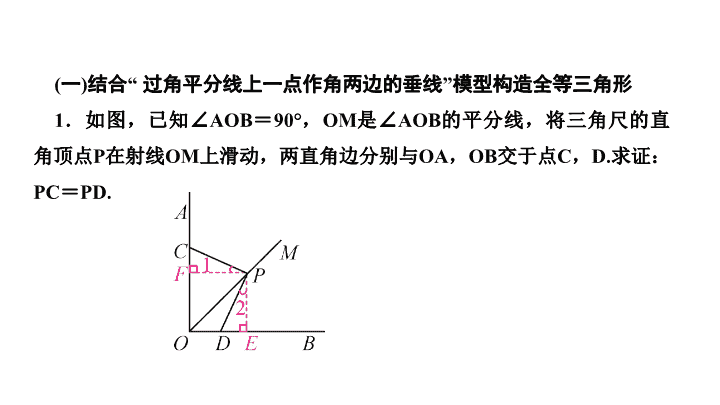
第十二章　全等三角形 人教版 专题训练(五)　作辅助线构造三角形全等的常见技巧 类型一　利用 “ 角平分线 ” 构造全等三角形 角平分线涉及的辅助线作法较多 ， 在本章中 ， 常用到的基本模型有如下三种 (AD 为∠ MAN 的平分线 ， 均有△ PAB≌△PAC) ： ( 一 ) 结合 “ 过角平分线上一点作角两边的垂线 ” 模型构造全等三角形 1 ．如图，已知∠ AOB ＝ 90° ， OM 是∠ AOB 的平分线，将三角尺的直角顶点 P 在射线 OM 上滑动，两直角边分别与 OA ， OB 交于点 C ， D. 求证： PC ＝ PD. 2 ．如图，在四边形 ABCD 中， BC ＞ BA ， AD ＝ CD ，若 BD 平分∠ ABC ，求证：∠ A ＋∠ C ＝ 180°. 方法2：结合“过角平分线上一点作角平分线的垂线”模型来构造全等三角形 3 ．如图， BD 是∠ ABC 的平分线， AD⊥BD ，垂足为 D ，求证：∠ BAD ＝∠ DAC ＋∠ C. 证明：延长 AD 交 BC 于点 E ，∵ AD⊥BD ，∴∠ ADB ＝∠ BDE ＝ 90°.∵BD 是∠ ABC 的平分线，∴∠ ABD ＝∠ EBD. 又∵ BD ＝ BD ， ∴△ ABD≌△EBD ，∴∠ BAD ＝∠ BED ，∵∠ BED ＝∠ DAC ＋∠ C ，∴∠ BAD ＝∠ DAC ＋∠ C 4 ．如图，在△ AOB 中， OA ＝ OB ，∠ AOB ＝ 90° ， BD 平分∠ ABO 交 OA 于点 D ， AE⊥BD 于点 E. 求证： BD ＝ 2AE. 类型二　利用 “ 截长补短法 ” 构造全等三角形 5 ．如图所示， AB∥CD ， BE ， CE 分别是∠ ABC ，∠ BCD 的平分线，点 E 在 AD 上，求证： BC ＝ AB ＋ CD.( 提示：在 BC 上截取 BF ，使 BF ＝ BA ，连接 EF) 证明：在 BC 上截取 BF ＝ AB ，连接 EF. 先用 SAS 证△ BAE≌△BFE ，得∠ A ＝∠ EFB. 又 AB∥CD ，∴∠ A ＋∠ D ＝ 180° ，又∠ EFB ＋∠ EFC ＝ 180° ，∴∠ D ＝∠ EFC ，再用 AAS 证△ EFC≌△EDC ，∴ FC ＝ CD ，∴ BC ＝ BF ＋ FC ＝ AB ＋ CD 6 ．如图，在△ ABC 中，∠ ABC ＝ 60° ， AD ， CE 分别平分∠ BAC ，∠ ACB ， AD ， CE 相交于点 O . (1) 求∠ AOC 的度数； (2) 求证： AC ＝ AE ＋ CD . 类型三　利用 “ 倍延法 ” 构造全等三角形 如果问题中的有关线段比较分散 ， 同时条件中又含有三角形的中线 ( 或中点 ) ， 此时常将中线 ( 或过中点的线段 ) 延长一倍后再与原三角形的某一顶点连接 ， 以构成 “ 8 ” 字形的全等三角形．方法 1 ：倍延中线 7 ．如图，在△ ABC 中， D 为 BC 的中点． (1) 求证： AB ＋ AC >2 AD ； (2) 若 AB ＝ 5 ， AC ＝ 3 ，求 AD 的取值范围． 解： (1) 证明：延长 AD 至点 E ，使 DE ＝ AD ，则 AE ＝ 2 AD ，连接 BE .∵ D 为 BC 中点，∴ CD ＝ BD ，又 AD ＝ ED ，∠ ADC ＝∠ EDB ，∴△ ADC ≌△ EDB (SAS) ，∴ BE ＝ AC ，∴ AB ＋ BE > AE ，∴ AB ＋ AC >2 AD (2)∵ AB － BE < AE < AB ＋ BE ，∴ AB － AC <2 AD < AB ＋ AC ，又 AB ＝ 5 ， AC ＝ 3 ，∴ 2<2 AD <8.∴1< AD <4 方法 2 ：倍延过中点的线段 8 ．如图，在△ ABC 中， D 是 BC 边上的中点， DE ⊥ DF ， DE 交 AB 于点 E ， DF 交 AC 于点 F ，连接 EF . 求证： BE ＋ CF ＞ EF . 类型四　根据 “ 一线三等角 ” 构造全等三角形 如图，两种基本模型中 “ 一线 ” 指直线 l ，“ 三等角 ” 指∠ BAC ＝∠ ADB ＝∠ AEC( 一般情况下都等于 90°) ， 则有结论∠ 1 ＝∠ 3 或∠ 2 ＝∠ 4. 9 ． 已知在△ ABC 中，∠ BAC ＝ 90° ， AB ＝ AC ，将△ ABC 放在平面直角坐标系中，如图所示． (1) 如图①，若 A(1 ， 0) ， B(0 ， 3) ，求 C 点坐标； (2) 如图②，若 A(1 ， 3) ， B( － 1 ， 0) ，求 C 点坐标； (3) 如图③，若 B( － 4 ， 0) ， C(0 ，－ 1) ，求 A 点坐标．