八年级上数学课件八年级上册数学课件《乘法公式》 人教新课标 (5)_人教新课标 31页

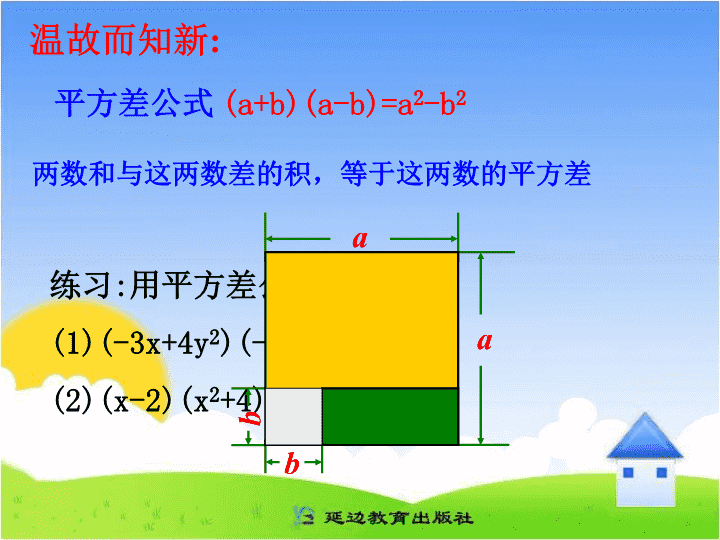
3.4 乘法公式(2) ---完全平方公式 平方差公式 练习:用平方差公式计算: (1)(-3x+4y2)(-4y2-3x) (2)(x-2)(x2+4)(x+2)(x4+16) (a+b)(a-b)=a2-b2 温故而知新: 两数和与这两数差的积，等于这两数的平方差 b a a b 49 25 64 40 运用多项式与多项式相乘的法则计 算下列各式： 1、(a+b)2 3、(2a+x)2 观察上述1、2两题的计算结果，你发现有什 么规律？你能用你的发现来猜测第3题的结果吗？ 合 作 学 习 =(a+b)(a+b) 2、(2+x)2 =(2+x)(2+x)= 22+2x+2x+x2 =(2a)2+2×2a•x+x2 =a2+ab+ab+b2 =a2+2ab+b2 =22+2×2x+x2 b ba a  2)( ba (a+b)² a² 2a b² 2b ab ab ab2+ + 完全平方和公式： 你能用一个图形的面积直观地表 示（a＋b）2的结果吗？ 完全平方公式: 两数和的平方,等于这两数的 平方和 , 加上这两数积的2倍. (a+b)2=a2+2ab+b2 一般的，我们有以下两数和的完全平方公式： 222 2)( bababa   2)32( yx计算： 2)2x（ 2)3( y)3)(2(2 yx 222 222 222 )()()(2)()3(3 )()()(2)()2()2( )()()(2)()2()1(    yx ya x ）（ 填空： 22 9124 yxyx  2 2 x x a2 a2 y y x x y3 y3 小明写出了如下的算式:(a−b)2 = [a+(−b)]2 他是怎么想的? 你能继续做下去吗? a2 −2ab+b2.(a−b)2= (a−b)2= [a+(−b)]2 = a2 +2a(-b)+ (−b)2 = a2 –2ab+ b2 a a b b (a-b)²  2)( ba 2a ab 2 22a ab b   a² ab ab ab 2b b² 完全平方差公式： 完全平方公式: 两数差的平方,等于这两数 的平方和,减去这两数积的2倍. n模仿练习： n（y－7）2＝ n （7－y ）2＝ (a+b)2=a2+2ab+b2 完全平方公式 和的完全平方公式与差的完全平方公式 统称完全平方公式. 平方差公式和完全平方公式也称乘法公式。 例3 运用完全平方公式计算： (1)(x+2y)2; (2)(2a-5)2; (3) (-2s+t)2; (4) (-3x-4y)2. 解：（1）原式=x2+2×x×2y+（2y）2 =x2+4xy+4y2 （2）原式=（2a）2-2×2a×5+52=4a2-20a+25 （3）原式=（-2s）2+2（-2s）t+t2=4s2-4st+t2 （4）原式=（-3x）2-2（-3x）4y+（4y）2 =9x2+24xy+16y2 (2)(-2a2+b)2 练习、运用完全平方公式计算： (1)( 4a2 - b2 )2 (3)(2a-3b)2-2a(a-b) 1、下面各式的计算是否正确？如果不正确，应 当怎样改正？ (2)(x -y)2 =x2 -y2 (3) (x -y)2 =x2-2xy -y2 (4) (x+2y)2 =x2 +2xy +2y2 (x +y)2 =x2+2xy +y2 (x -y)2 =x2 -2xy +y2 （1）(x+y)2=x2 +y2 (2) (a - b)2 与 (b - a)2 (1) (-a -b)2 与(a+b)2 2、比较下列各式之间的关系： （3）(-b +a)2 与(-a +b)2 互为相反数的两式的完全平方结果一样。 4.在横线上填入适当的整式: 22 22 22 )15(_____1025).3( )32(9_______4).2( )7(49_______).1(    xxx xx xx 14x 12x 1 引例:一花农有1块正方形茶花苗圃，边长 为a（m）。现将这块苗圃的边长都增加 1.5m，求这块苗圃的面积增加了多少m²。 (a+1.5)²-a² =a²+3a+2.25-a² = 3a+2.25 例4、一花农有4块正方 形茶花苗圃,边长分别 为 30.1 m , 29.5 m, 30m, 27m. 现将这4块苗圃的 边长都增加1.5m后,求各苗圃的面 积分别增加了多少m2? 生活在线： 解：设原正方形苗圃的边长为a (m)，边长增加1.5m后，新正方 形的边长为(a+1.5) m。 (a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25 当a=30.1时，3a+2.25=3×30.1+2.25=92.55 当a=29.5时，3a+2.25=3×29.5+2.25=90.75 当a=30 时，3a+2.25=3×30 +2.25=92.25 当a=27 时，3a+2.25=3×27 +2.25=83.25 答：4块茶花苗圃的面积分别增加了92.55m2，90.75m2，92.25m2， 83.25m2。 例4、花农老万有4块正方形菜花苗圃，边长分别为30.1m， 29.5m，30m，27m。现将这4块苗圃的边长都增加1.5m， 求各 苗圃的面积分别增加多少m2？ 练习：利用完全平方公式计算： (1) 0.982 (2) 10012 解：(1) 原式 = （ 1 − 0.02）2 = 12 − 2 ×1×0.02 + 0.022 = 1 − 0.04 + 0.0004 = 0.9604 （2）原式 = （ 1000 + 1 ）2 = 10002 + 2 × 1000×1 + 12 = 1000000 + 2000 + 1 =1002001 完全平方公式   222 2 bababa    222 2 bababa  口诀：首平方，尾平方，首尾两倍放中央 完全平方公式： 222 2)( bababa  1).不漏中间项。2).注意中间项的符号对应。 3).乘方时应适当添括号 注意完全平方公式和平方差公式不同： 形式不同:平方差公式是两数和与两数差的积 完全平方公式的两数和的平方 结果不同： 完全平方公式的结果 是三项， 即 (a b)2＝a2 2ab+b2; 平方差公式的结果 是两项， 即 (a+b)(a−b)＝a2−b2. (3)用简便的方法计算: 23452+0.76552+2.469×0.7655 _____199)2( 2 简便计算： 做一做： (4)如果x2+ax+36是一个完全平方式,那么a=______ (6)已知(a+b)2=11,ab=1,求(a-b)2的值. 做一做： (5)如果x2+6x+b2是一个完全平方式,那么b= ； ±12 ±3 计算： 22 ) 2 1)(1( a )1)(1)(2(  xx 2))(3( cba  提高拓展： 生活在线：要给一边长为a米的正方 形桌子辅上正方形的桌布,桌布的四周均 超出桌面0.1米,问需要多大面积的桌布. 解:由题意知,桌布是边长为(a+0.2)米的正 方形,故面积为: (a+0.2 )2 = a2 +0.4a+0.04(平方米) 答:所需桌布的面积为a2 +0.4a+0.04(平方米) 着手点:1.桌布的形状 2.边长多少? 生活在线：小红用5块工艺布料制作靠垫面子,如 图甲,其中四周的4块由如图乙的长方形布料裁成4块 得到,正中的一块从另一块布料裁得.正中一块正方形 布料应裁取多大的面积(接缝忽略不计) 分析:中间面积 =总面积-周围面积 解:由图得,大正方形的边长为 , 2 2 2 2 baba    2) 2 2 2 2( baba    )2)(2( baba  2 222 )4(4 b baa   答:中间正方形的面积应取 2b 更多教学资源下载: http://zhdduya100.taobao.co m/