北师大版数学八年级上册《探索勾股定理》练习 3页

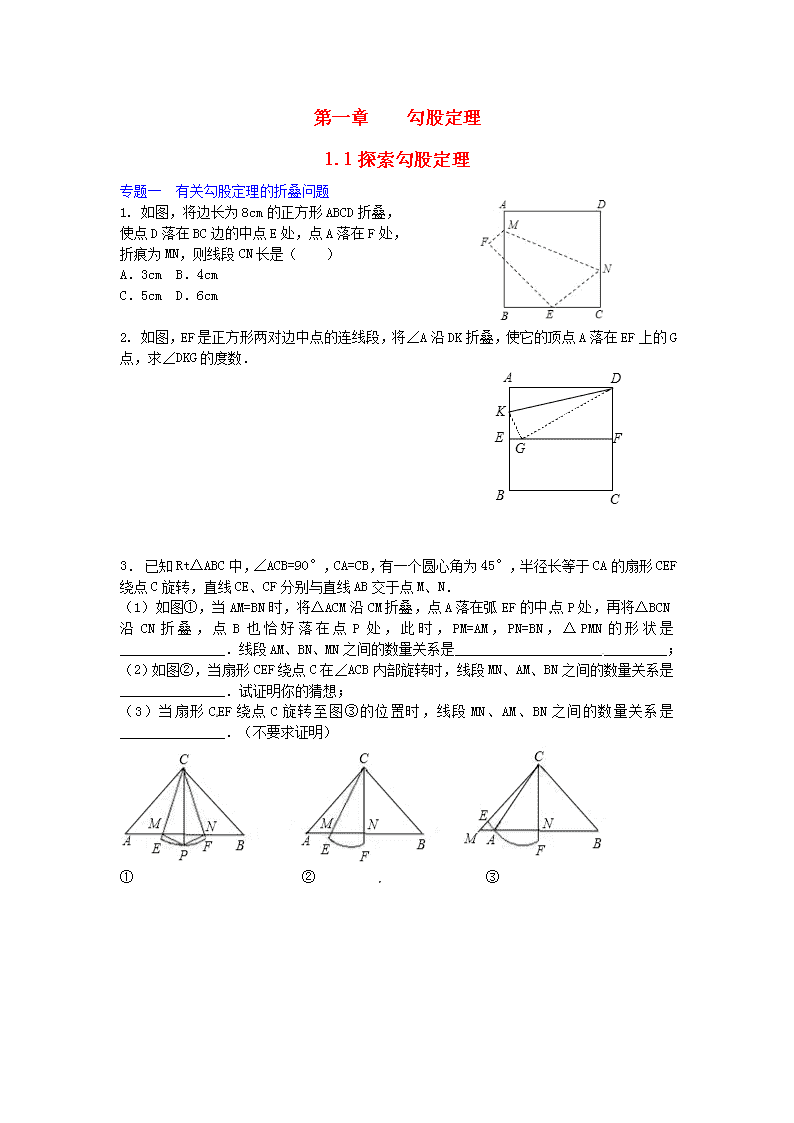
第一章 勾股定理 1.1 探索勾股定理 专题一 有关勾股定理的折叠问题 1. 如图，将边长为 8cm 的正方形 ABCD 折叠， 使点 D 落在 BC 边的中点 E 处，点 A 落在 F 处， 折痕为 MN，则线段 CN 长是（ ） A．3cm B．4cm C．5cm D．6cm 2. 如图，EF 是正方形两对边中点的连线段，将∠A 沿 DK 折叠，使它的顶点 A 落在 EF 上的 G 点，求∠DKG 的度数． 3． 已知 Rt△ABC 中，∠ACB=90°，CA=CB，有一个圆心角为 45°，半径长等于 CA 的扇形 CEF 绕点 C 旋转，直线 CE、CF 分别与直线 AB 交于点 M、N． （1）如图①，当 AM=BN 时，将△ACM 沿 CM 折叠，点 A 落在弧 EF 的中 点 P 处，再将△BCN 沿 CN 折叠，点 B 也恰好落在点 P 处，此时，PM=AM，PN=BN，△PMN 的形状是_______________．线 段 AM、BN、MN 之间的数量关系是______________________________； （2）如图②，当扇形 CEF 绕点 C 在∠ACB 内部旋转时，线段 MN、AM、BN 之间的数量关系是 _______________．试证明你的猜想； （3）当扇形 C EF 绕点 C 旋转至图③的位置时，线段 MN、AM、BN 之间的数量关系是 _______________．（不要求证明） ① ② ③ 专题二 勾股定理的证明 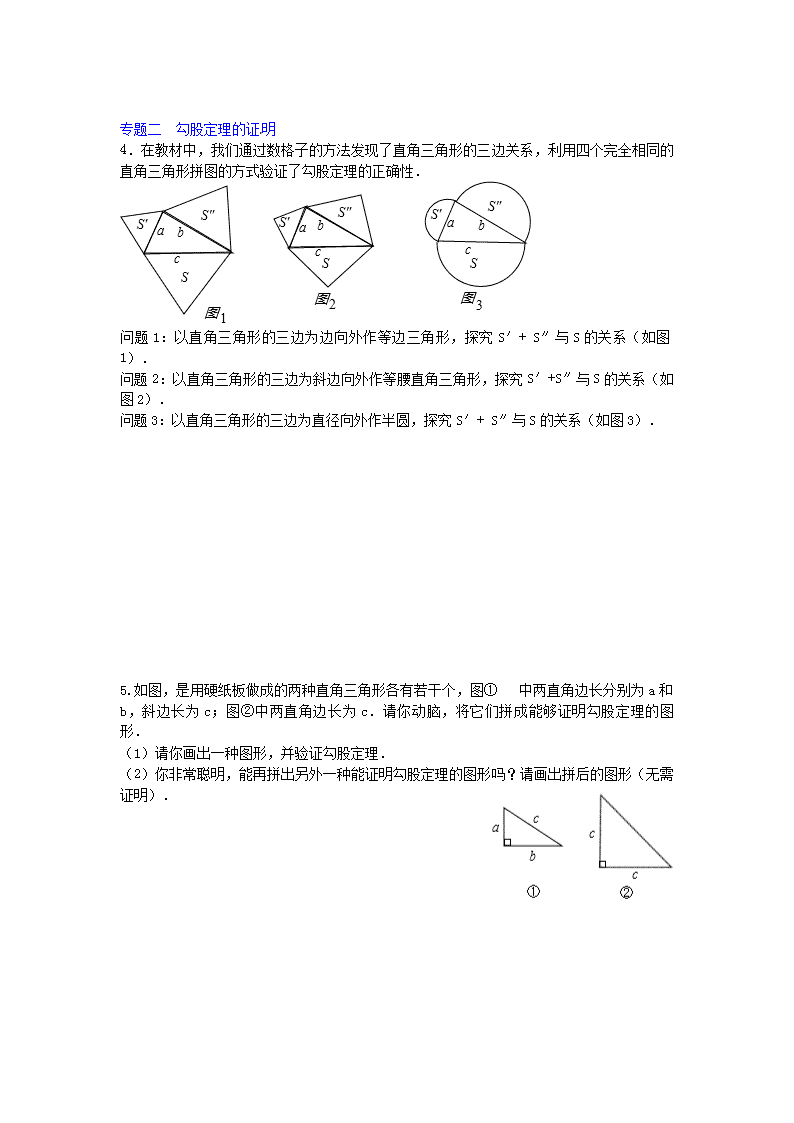4．在教材中，我们通过数格子的方法发现了直角三角形的三边关系，利用四个完全相同的 直角三角形拼图的方式验证了勾股定理的正确性． 问题 1：以直角三角形的三边为边向外作等边三角形，探究 S′+ S″与 S 的关系（如图 1）． 问题 2：以直角三角形的三边为斜边向外作等腰直角三角形，探究 S′+S″与 S 的关系（如 图 2）． 问题 3：以直角三角形的三边为直径向外作半圆，探究 S′+ S″与 S 的关系（如图 3）． 5. 如图，是用硬纸板做成的两种直角三角形各有若干个，图① 中两直角边长分别为 a 和 b，斜边长为 c；图②中两直角边长为 c．请你动脑，将它们拼成能够证明勾股定理的图 形． （1）请你画出一种图形，并验证勾股定理． （2）你非常聪明，能再拼出另外一种能证明勾股定理的图形吗？请画出拼后的图形（无需 证明）． 答案： 1．A 【解析】设 CN=x cm，则 DN=（8-x）cm. 由折叠的性质知 EN=DN=（8-x）cm， 而 EC= 1 2 BC=4 cm，在 Rt△ECN 中，由勾股定理可知 EN2=EC2+CN2，即（8-x）2=16+x2， 整理得 16x=48，所以 x=3．故选 A． 2．解：∵DF= 1 2 CD= 1 2 DG，∴∠DGF=30°．∵∠EKG+∠KGE=90°，∠KGE+∠DGF=90°， ∴∠EKG=∠DGF=30°．∵2∠DKG+∠GKE=180°，∴∠DKG=75°． 3．解：（1）根据折叠的性质知：△CAM≌△CPM，△CNB≌△CNP．∴AM=PM，∠A=∠CPM，PN=NB， ∠B=∠CPN. ∴∠MPN=∠A+∠B=90°，PM=PN=AM=BN. 故△PMN 是等腰直角三角形，AM2+BN2=MN2（或 AM=BN= 2 2 MN）． （2）AM2+BN2=MN2. 证明:如图,将△ACM 沿 CM 折叠，得△DCM，连 DN， 则△ACM≌△DCM，∴CD=CA，DM=AM，∠DCM=∠ACM. 同理可知∠DCN=∠BCN，△DCN≌△BCN，DN=BN， 而∠MDC=∠A=45°，∠CDN=∠B=45°，∴∠MDN=90°， ∴DM2+DN2=MN2，故 AM2+BN2=MN2． （3）AM2+BN2=MN2；解法同（2）． 4．解：探究 1：由等边三角形的性质知：S′= 3 4 a2，S″= 3 4 b2，S= 3 4 c2， 则 S′+ S″= 3 4 （a2+b2）.因为 a2+b2=c2，所以 S′+ S″=S． 探究 2：由等腰直角三角形的性质知：S′= 1 4 a2，S″= 1 4 b2，S= 1 4 c2． 则 S′+S″= 1 4 （a2+b2）.因为 a2+b2=c2，所以 S′+S″=S． 探究 3：由圆的面积计算公式知：S′= 1 8 πa2，S″= 1 8 πb2，S= 1 8 πc2． 则 S′+ S″= 1 8 π（a2+b2），因为 a2+b2=c2，所以 S′+ S″=S． 5．解：（1）如图所示， 根据正方形的面积可得（a+b）2=4× 1 2 ab+c2， 即 a2+b2=c2． （2）如图所示．