- 112.50 KB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
命题
课题
§13.1.1 命题
授课人
教
学
目
标
知识技能
了解命题的概念,能说出命题的条件和结论,知道什么是真命题和假命题.
数学思考
在探索命题概念中,体会研究问题的方法,感受抽象数学概念的过程.
问题解决
探索并了解命题的概念,分清命题的条件和结论,辨别命题的真假.
情感态度
以问题的解决为中心,树立学生在探索中形成正确表达自己的观点的信心.
教学
重点
对命题结构的认识.
教学
难点
举反例说明一个命题是假命题.
授课
类型
新授课
课时
第一课时
教具
多媒体课件
教学活动
教学
步骤
师生活动
设计意图
回顾
思考:请判断下列语句的真假,能否看出这些语句的表达形式有什么特点?
(1)若直线a∥b,则直线a和直线b无公共点;
(2)2+4=7;
(3)垂直于同一条直线的两个平面平行;
(4)若x2=1,则x=1.
回顾旧知,为讲解新知识做铺垫.
活动
一:
创设
情境
导入
新课
【课堂引入】
看下列图形,根据图形说一说由这些图形你想到了些什么:
图13-1-
学生活动:每个学生根据图形,把所发现的图形的特点都写出来,每个图至少都要写一条,越多越好.
创设情境,激发学生兴趣,引出本节要讨论的内容.
活动
二:
实践
探究
交流
新知
【探究】
探究1 命题的概念及构成
1.师生共同活动:结合学生写的图形的特点及课本中(出示PPT)的命题,归纳出命题的概念.
概念(板书):判断某一件事情的语句叫做命题.
2.观察前面的命题思考:
问题:命题的结构有什么特征?
引导学生归纳总结:
(1)在数学中
4
,许多命题是由题设(或已知条件)、结论两部分组成的.
题设是已知事项;结论是由已知事项推出的事项,
(2)命题通常可写成“如果……,那么……”的形式.
用“如果”开始的部分就是题设,而用“那么”开始的部分就是结论.
例如:命题“如果两条直线都与第三条直线平行,那么这两条直线也互相平行.”的题设是两条直线都与第三条直线平行,结论是这两条直线也互相平行.
(3)有的命题的题设与结论不十分明显,可以将它写成“如果……,那么……”的形式,就可以分清它的题设和结论了.
例如,命题“对顶角相等”可写成“如果两个角是对顶角,那么这两个角相等.”
探究2 真、假命题
问题:判断下列语句是不是命题,是命题的指出命题的题设和结论,并判断此命题是否正确.
(1)如果两条直线相交,那么它们只有一个交点;
(2)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;
(3)相等的角是对顶角;
(4)任意两个直角都相等;
学生在独立思考,合作交流后得出:
四个语句都是命题;
命题(1)的条件是两条直线相交,结论是它们只有一个交点;
命题(2)的条件是两条直线被第三条直线所截形成的同旁内角互补,结论是这两条直线平行
命题(3)的条件是两个角相等,结论是它们对顶角;
命题(4)的条件是两个角是直角,结论是它们相等;
要判断一个命题是真命题,可以用逻辑推理的方法加以论证;而要判断一个命题是假命题,只要举出一个例子,说明该命题不成立,即只要举出一个符合该命题题设而不符合该命题结论的例子就可以了,在数学中,这种方法称为“举反例”
探究3 把命题改写成如果……,那么……
(1)对顶角相等;
(2)同角的余角相等;
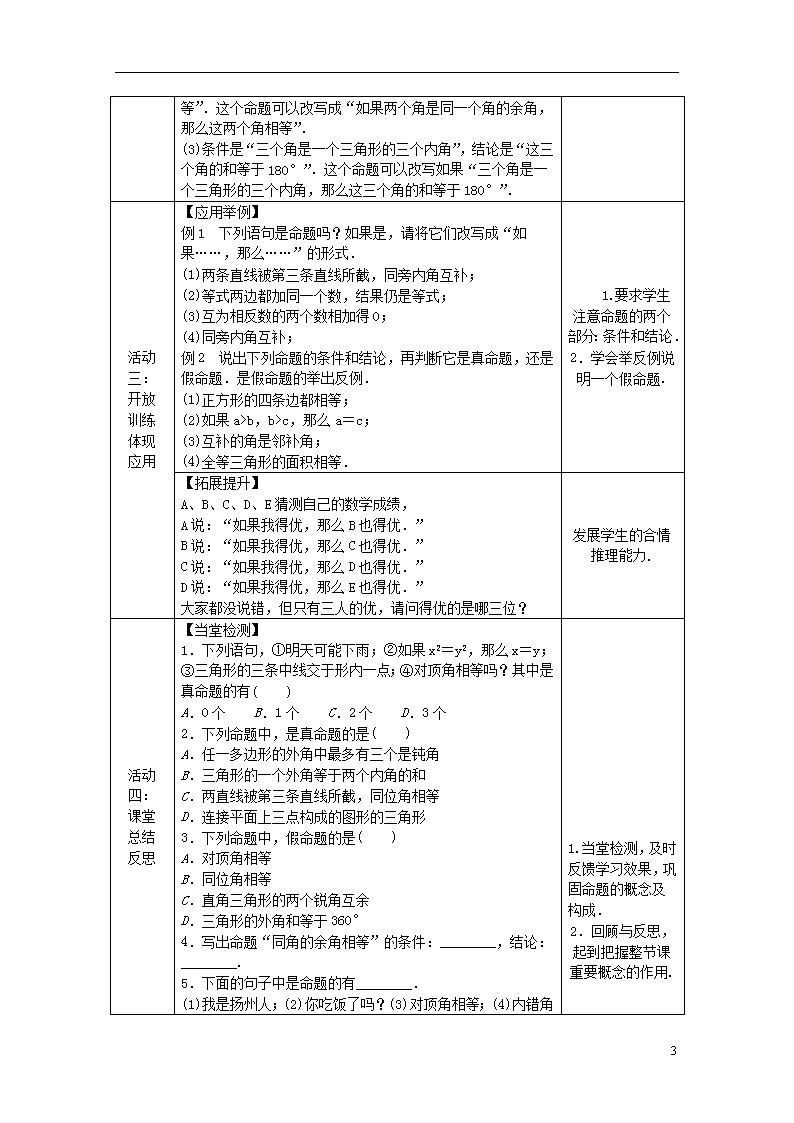
(3)三角形的内角和等于180°;
分析:找出命题的条件和结论是本节课的难点,因为命题在叙述时要求通顺和简练,把命题中的有些词或句子省略了,在改写是注意把时要把省略的词或句子添加上去.
(1)可作如下启发:对顶角指两个角的关系,相等指两个角相等.把“两个角”添补上去,写成“是对顶角的两个角相等”,这样学生不难得出这个命题的条件是“两个角是对顶角”,结论是“两个角相等”.这个命题可以改写成“如果两个角是对顶角,那么这两个角相等”.
(2)条件是“两个角是同一个角的余角”,
从实例出发,了解命题的概念.判断命题的真假是数学学习的重要环节,务必让学生学会分析.
4
结论是“这两个角相等”.这个命题可以改写成“如果两个角是同一个角的余角,那么这两个角相等”.
(3)条件是“三个角是一个三角形的三个内角”,结论是“这三个角的和等于180°”.这个命题可以改写如果“三个角是一个三角形的三个内角,那么这三个角的和等于180°”.
活动
三:
开放
训练
体现
应用
【应用举例】
例1 下列语句是命题吗?如果是,请将它们改写成“如果……,那么……”的形式.
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
例2 说出下列命题的条件和结论,再判断它是真命题,还是假命题.是假命题的举出反例.
(1)正方形的四条边都相等;
(2)如果a>b,b>c,那么a=c;
(3)互补的角是邻补角;
(4)全等三角形的面积相等.
1.要求学生注意命题的两个部分:条件和结论.
2.学会举反例说明一个假命题.
【拓展提升】
A、B、C、D、E猜测自己的数学成绩,
A说:“如果我得优,那么B也得优.”
B说:“如果我得优,那么C也得优.”
C说:“如果我得优,那么D也得优.”
D说:“如果我得优,那么E也得优.”
大家都没说错,但只有三人的优,请问得优的是哪三位?
发展学生的合情推理能力.
活动
四:
课堂
总结
反思
【当堂检测】
1.下列语句,①明天可能下雨;②如果x2=y2,那么x=y;③三角形的三条中线交于形内一点;④对顶角相等吗?其中是真命题的有( )
A.0个 B.1个 C.2个 D.3个
2.下列命题中,是真命题的是( )
A.任一多边形的外角中最多有三个是钝角
B.三角形的一个外角等于两个内角的和
C.两直线被第三条直线所截,同位角相等
D.连接平面上三点构成的图形的三角形
3.下列命题中,假命题的是( )
A.对顶角相等
B.同位角相等
C.直角三角形的两个锐角互余
D.三角形的外角和等于360°
4.写出命题“同角的余角相等”的条件:________,结论:________.
5.下面的句子中是命题的有________.
1.当堂检测,及时反馈学习效果,巩固命题的概念及构成.
2.回顾与反思,起到把握整节课重要概念的作用.
4
(1)我是扬州人;(2)你吃饭了吗?(3)对顶角相等;(4)内错角相等;(5)延长线段AB;(6)明天可能下雨;(7)若a2>b2,则a>b.
6.把下列命题改为“如果……那么……”的形式.
(1)垂直于同一直线的两直线互相平行.________
(2)末位数是偶数的整数被2整除.________
7.举起一个反例说明下列命题是假命题.
(1)相等的角是同位角;
(2)大于90°的角为钝角.
回顾与反思
1.同学们想一想,今天学习了哪些知识?
2.为什么全等三角形的对应边相等、对应角相等?
布置作业,专题突破
课本P55练习第1,2题.
【知识网络】
框架图式总结,更容易形成知识网络.
【教学反思】
①[授课流程反思]
A.新课导入□ B.情景导入□
命题的构成中,要注意引导学生去发现,在把命题改写成“如果……那么……”的时候,要注意示范,指出学生表达不合理的地方.
②[讲授效果反思]
A.重点□ B.难点□ C.易错点□
教师要帮助学生总结:本节课看似新课,实是对前阶段几何内容的一次重要的梳理,也是对以前所学内容的回顾,教师可抓住这个机会,在学习新内容的基础上巩固以前的重要知识,让学生在不知不觉的状态下循序渐进.
③[师生互动反思]
学生回顾本节知识时,教师要注意组织学生谈个人收获,师生要共同交流.
④[习题反思]
好题题号__________________________________________
错题题号__________________________________________
教学反思进一步提升教师教学能力.
4
相关文档
- 初中语文部编版八年级下册期末总复2021-11-016页
- 2020人教版初中数学八年级上学期知2021-11-0160页
- 初中语文八年级上册课内外古诗词赏2021-11-015页
- 北师大版初中数学确定一次函数表达2021-11-014页
- 初中数学八年级上册第十二章全等三2021-11-014页
- 2018年达利教育卓越奖初中学科竞赛2021-11-016页
- 初中8年级语文教案:第11讲 议论文之2021-11-019页
- 初中数学八年级上册第十二章全等三2021-11-014页
- 初中8年级物理教案:第06讲 滑轮速度2021-11-0119页
- 浙江省海宁市初中第三教研片2013-22021-11-0110页