八年级数学下册知能提升作业二十六第20章平行四边形的判定20 5页

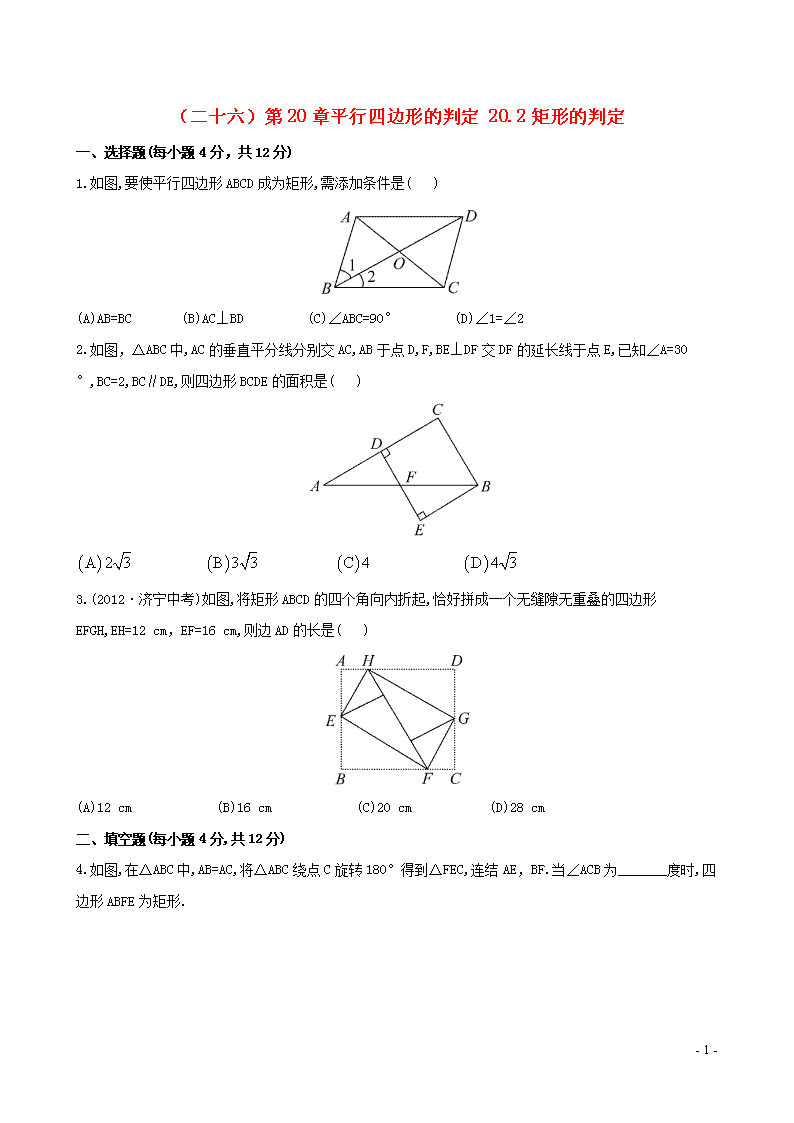
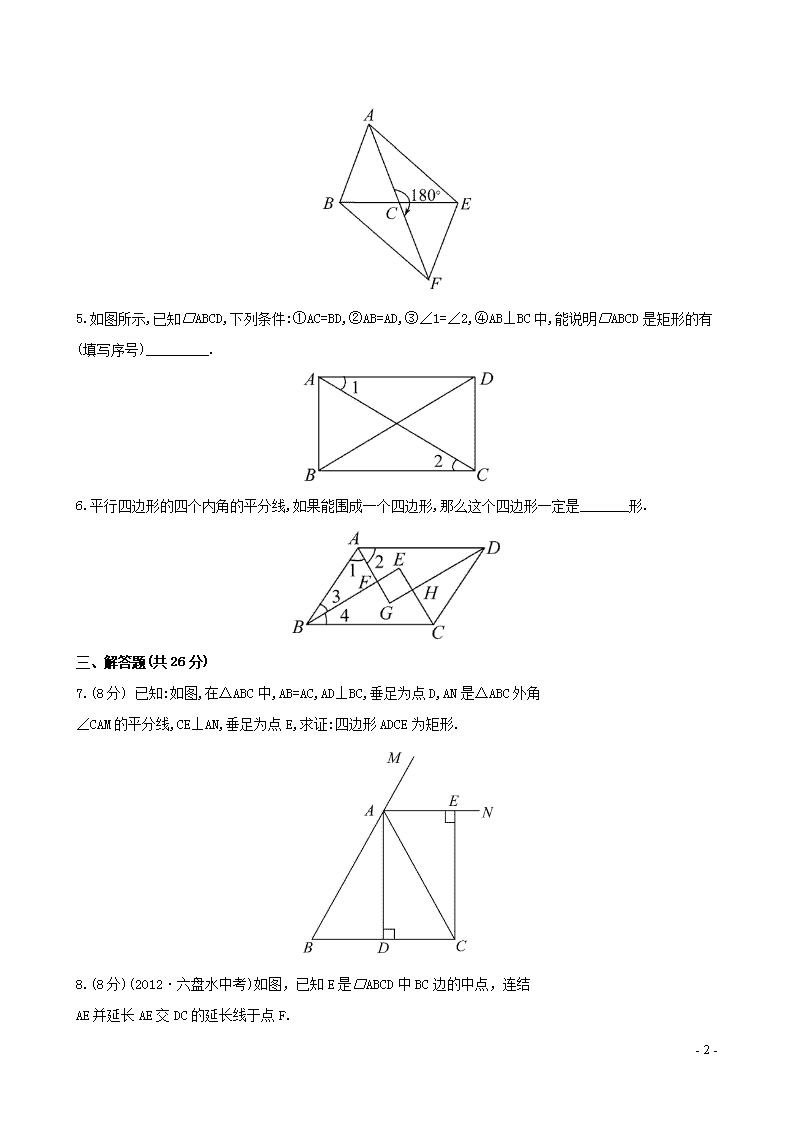
‎（二十六）第20章平行四边形的判定 20.2矩形的判定 一、选择题(每小题4分，共12分)‎ ‎1.如图,要使平行四边形ABCD成为矩形,需添加条件是( )‎ ‎(A)AB=BC (B)AC⊥BD (C)∠ABC=90° (D)∠1=∠2‎ ‎2.如图，△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,BC∥DE,则四边形BCDE的面积是( )‎ ‎3.(2012·济宁中考)如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12 cm，EF=16 cm,则边AD的长是( )‎ ‎(A)12 cm (B)16 cm (C)20 cm (D)28 cm 二、填空题(每小题4分,共12分)‎ ‎4.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连结AE，BF.当∠ACB为_______度时,四边形ABFE为矩形.‎ - 5 -‎ ‎5.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明□ABCD是矩形的有(填写序号)_________.‎ ‎6.平行四边形的四个内角的平分线,如果能围成一个四边形,那么这个四边形一定是_______形.‎ 三、解答题(共26分)‎ ‎7.(8分) 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角 ‎∠CAM的平分线,CE⊥AN,垂足为点E,求证:四边形ADCE为矩形.‎ ‎8.(8分)(2012·六盘水中考)如图，已知E是□ABCD中BC边的中点，连结 AE并延长AE交DC的延长线于点F.‎ - 5 -‎ ‎(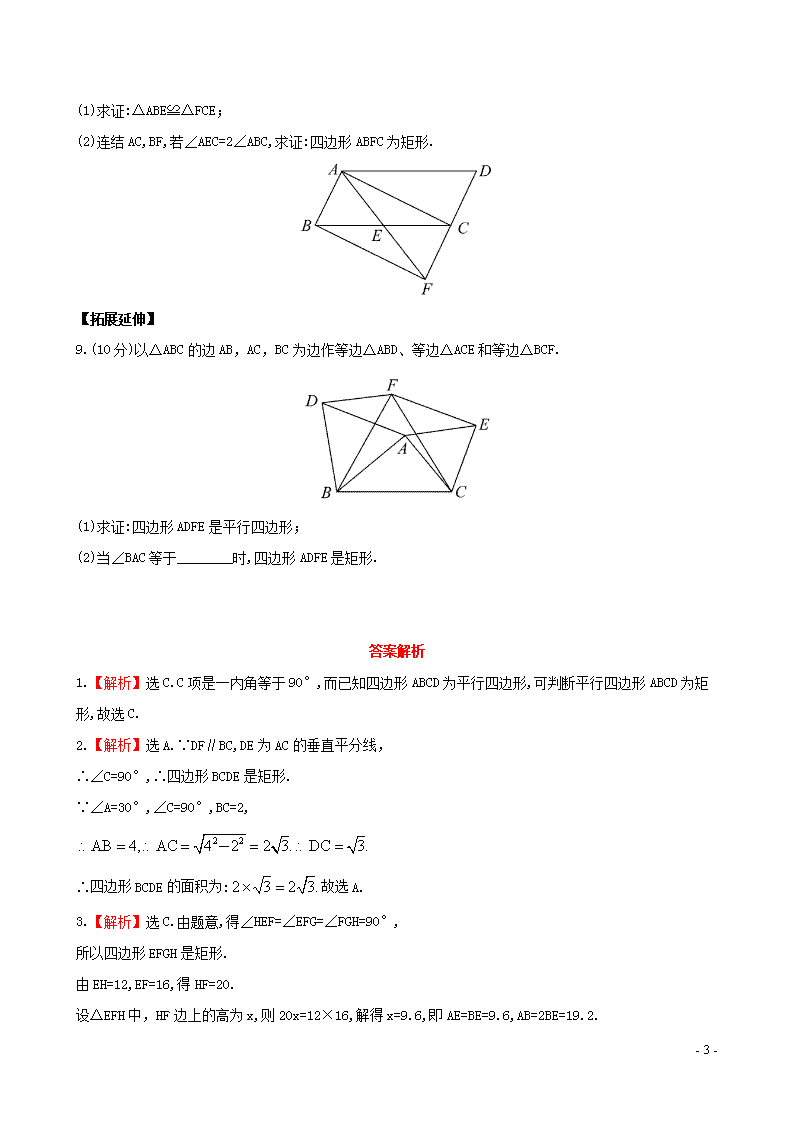1)求证:△ABE≌△FCE；‎ ‎(2)连结AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.‎ ‎【拓展延伸】‎ ‎9.(10分)以△ABC的边AB，AC，BC为边作等边△ABD、等边△ACE和等边△BCF.‎ ‎(1)求证:四边形ADFE是平行四边形；‎ ‎(2)当∠BAC等于________时,四边形ADFE是矩形.‎ 答案解析 ‎1.【解析】选C.C项是一内角等于90°,而已知四边形ABCD为平行四边形,可判断平行四边形ABCD为矩形,故选C.‎ ‎2.【解析】选A.∵DF∥BC,DE为AC的垂直平分线，‎ ‎∴∠C=90°,∴四边形BCDE是矩形.‎ ‎∵∠A=30°,∠C=90°,BC=2,‎ ‎∴四边形BCDE的面积为:故选A.‎ ‎3.【解析】选C.由题意,得∠HEF=∠EFG=∠FGH=90°,‎ 所以四边形EFGH是矩形.‎ 由EH=12,EF=16,得HF=20.‎ 设△EFH中，HF边上的高为x,则20x=12×16,解得x=9.6,即AE=BE=9.6,AB=2BE=19.2.‎ - 5 -‎ 由题意,得矩形ABCD的面积为矩形EFGH面积的2倍，所以AB×AD=2×EF×EH，即19.2×AD=2×16×12,解得AD=20，即AD的长是20 cm,故选C.‎ ‎4.【解析】∵△ABC≌△FEC,‎ ‎∴AB=FE,∠BAC=∠EFC.‎ ‎∴AB∥FE,∴四边形ABFE为平行四边形.‎ 如果□ABFE为矩形,则需AF=BE,需AC=BC.又因为AC=AB,那么三角形ABC是等边三角形,所以∠ACB=60°.‎ 答案：60‎ ‎5.【解析】根据矩形的判断方法,能说明□ABCD是矩形的有:①对角线相等的平行四边形是矩形；④有一个角是直角的平行四边形是矩形.‎ 答案：①④‎ ‎6.【解析】根据图形,有∠1=∠2,∠3=∠4.‎ 又∵AD∥BC,∴∠BAD+∠ABC=180°,‎ ‎∴∠1+∠3=90°,∴∠AFB=∠EFG=90°,‎ 同理,平行四边形的相邻角的平分线一定互相垂直,‎ 因而平行四边形的四个内角的平分线,如果能围成四边形,四边形的四个内角一定是直角,即四边形是矩形.‎ 答案：矩 ‎7.【证明】在△ABC中,AB=AC,AD⊥BC,‎ ‎∴∠BAD=∠DAC,‎ ‎∵AN是△ABC外角∠CAM的平分线,‎ ‎∴∠MAE=∠CAE,‎ ‎∴∠DAE=∠DAC+∠CAE=×180°=90°,‎ 又∵AD⊥BC,CE⊥AN,‎ ‎∴∠ADC=∠CEA=90°,‎ ‎∴四边形ADCE为矩形.‎ ‎8.【证明】(1)∵E是BC的中点,‎ ‎∴BE=CE.‎ ‎∵四边形ABCD是平行四边形,‎ ‎∴AB∥DF,‎ ‎∴∠BAE=∠CFE.‎ 在△ABE与△FCE中 - 5 -‎ ‎∴△ABE≌△FCE(A.A.S.).‎ ‎(2)∵∠AEC=∠ABE+∠BAE,‎ ‎∠AEC=2∠ABC,‎ ‎∴∠ABE=∠BAE,‎ ‎∴AE=BE.‎ ‎∵△ABE≌△FCE,‎ ‎∴AE=EF,又BE=CE,‎ ‎∴AE=EF=BE=CE,‎ 即AF=BC,‎ ‎∴四边形ABFC为矩形.‎ ‎9.【解析】(1)∵△ABD, △ACE,△BCF是等边三角形,‎ ‎∴ BD=BA,BF=BC,AC=AE,∠DBA=∠CBF=60°,‎ ‎∴∠DBA-∠ABF=∠CBF-∠ABF,‎ ‎∴∠DBF=∠CBA,‎ ‎∴△BDF≌△BAC,‎ ‎∴DF=AC.即DF=AE；‎ 同理,可证EF=AD,‎ ‎∴四边形ADFE是平行四边形；‎ ‎(2)当∠BAC=150°时,四边形ADFE是矩形.‎ ‎∵∠DAB=∠CAE=60°,‎ ‎∴当∠BAC=150°时,∠DAE=90°,‎ ‎∴四边形ADFE是矩形.‎ - 5 -‎