八年级上册数学期中考试 20页

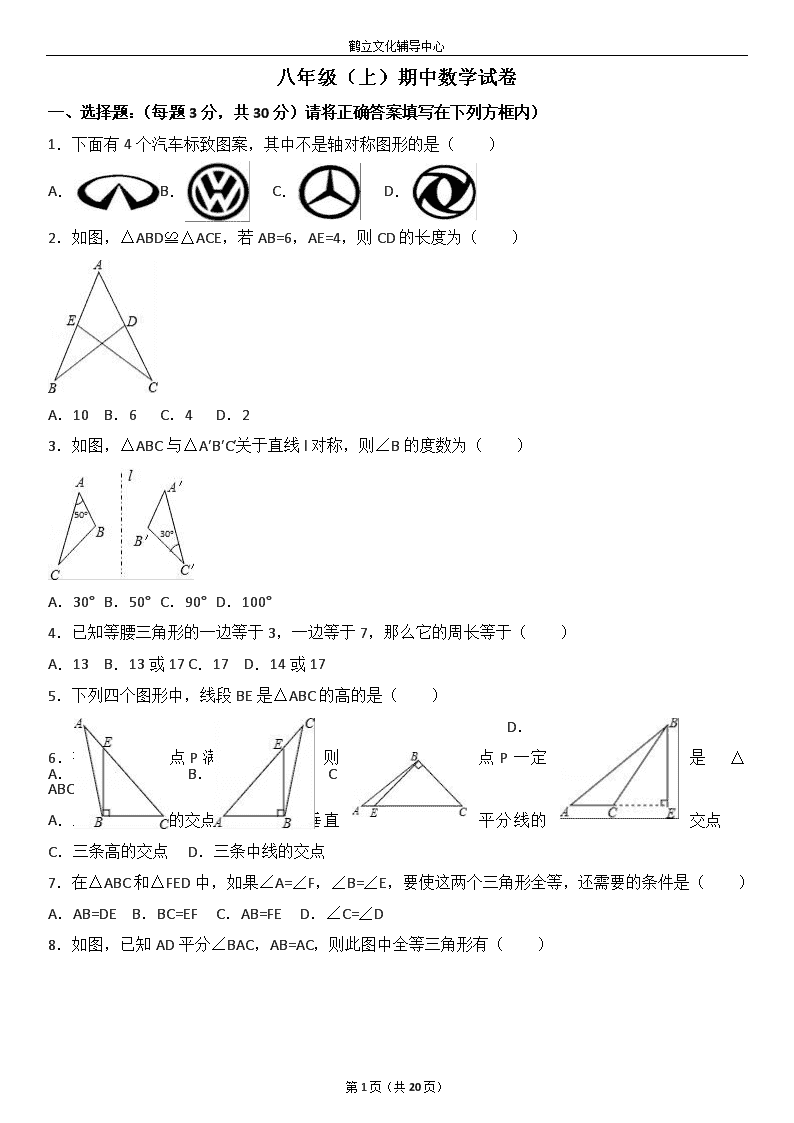
鹤立文化辅导中心 八年级（上）期中数学试卷 一、选择题：（每题3分，共30分）请将正确答案填写在下列方框内）‎ ‎1．下面有4个汽车标致图案，其中不是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎2．如图，△ABD≌△ACE，若AB=6，AE=4，则CD的长度为（　　）‎ A．10 B．6 C．4 D．2‎ ‎3．如图，△ABC与△A′B′C′关于直线l对称，则∠B的度数为（　　）‎ A．30° B．50° C．90° D．100°‎ ‎4．已知等腰三角形的一边等于3，一边等于7，那么它的周长等于（　　）‎ A．13 B．13或17 C．17 D．14或17‎ ‎5．下列四个图形中，线段BE是△ABC的高的是（　　）‎ A． B． C D．‎ ‎6．在△ABC内一点P满足PA=PB=PC，则点P一定是△ABC（　　）‎ A．三条角平分线的交点 B．三边垂直平分线的交点 C．三条高的交点 D．三条中线的交点 ‎7．在△ABC和△FED中，如果∠A=∠F，∠B=∠E，要使这两个三角形全等，还需要的条件是（　　）‎ A．AB=DE B．BC=EF C．AB=FE D．∠C=∠D ‎8．如图，已知AD平分∠BAC，AB=AC，则此图中全等三角形有（　　）‎ 第20页（共20页）‎ 鹤立文化辅导中心 A．2对 B．3 对 C．4对 D．5对 ‎9．AD是△ABC的中线，DE=DF．下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎10．已知AB=AC=BD，则∠1与∠2的关系是（　　）‎ A．∠1=2∠2 B．2∠1+∠2=180° C．∠1+3∠2=180° D．3∠1﹣∠2=180°‎ ‎　‎ 二．填空题（3x8=24分）‎ ‎11．已知过一个多边形的某一顶点共可作2015条对角线，则这个多边形的边数是　　．‎ ‎12．如图，在△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD的周长为20cm，AE=5cm，则△ABC的周长是　　cm．‎ ‎13．将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为　　度．‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎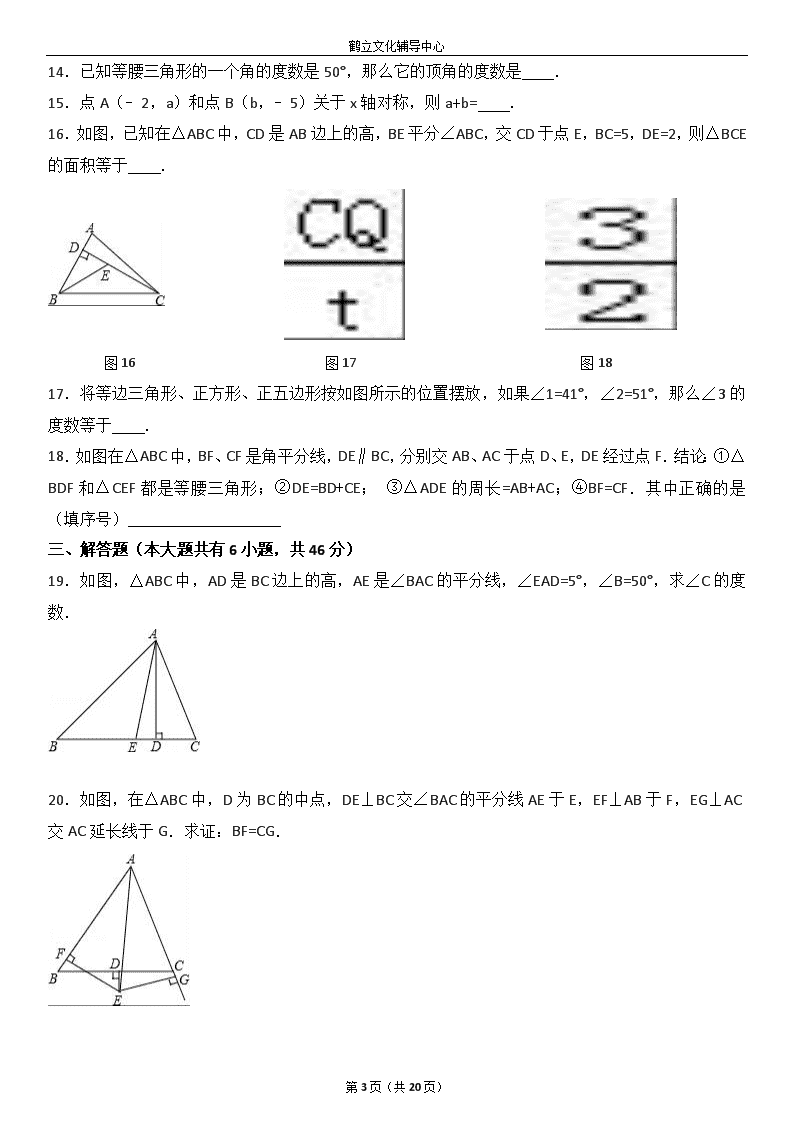14．已知等腰三角形的一个角的度数是50°，那么它的顶角的度数是　　．‎ ‎15．点A（﹣2，a）和点B（b，﹣5）关于x轴对称，则a+b=　　．‎ ‎16．如图，已知在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于　　．‎ ‎ ‎ 图16 图17 图18‎ ‎17．将等边三角形、正方形、正五边形按如图所示的位置摆放，如果∠1=41°，∠2=51°，那么∠3的度数等于　　．‎ ‎18．如图在△ABC中，BF、CF是角平分线，DE∥BC，分别交AB、AC于点D、E，DE经过点F．结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE； ③△ADE的周长=AB+AC；④BF=CF．其中正确的是　　（填序号） ‎ 三、解答题（本大题共有6小题，共46分）‎ ‎19．如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠EAD=5°，∠B=50°，求∠C的度数．‎ ‎20．如图，在△ABC中，D为BC的中点，DE⊥BC交∠BAC的平分线AE于E，EF⊥AB于F，EG⊥AC交AC延长线于G．求证：BF=CG．‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎21．（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；‎ ‎（2）直接写出A′，B′，C′三点的坐标：A′（　　），B′（　　），C′（　　）．‎ ‎（3）计算△ABC的面积． ‎22．如图，点D，E在△ABC的边BC上，连接AD，AE．①AB=AC；②AD=AE；③BD=CE以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：A：①②⇒③； B：①③⇒②； C：②③⇒①‎ 请选择一个真命题　　 进行证明（先写出所选命题，然后证明）．‎ ‎23．如图，线段AC、BD交于点M，过B、D两点分别作AC的垂线段BF、DE，AB=CD ‎（1）若∠A=∠C，求证：FM=EM；‎ ‎（2）若FM=EM，则∠A=∠C．是真命题吗？（直接判断，不必证明）‎ ‎24．如图，已知△ABC中，∠B=∠C，AB=8厘米，BC=6厘米，点D为AB的中点．如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t（秒）（0≤t≤3）．‎ ‎（1）用的代数式表示PC的长度；‎ ‎（2）若点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；‎ ‎（3）若点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？‎ ‎　‎ 第20页（共20页）‎ 鹤立文化辅导中心 第20页（共20页）‎ 鹤立文化辅导中心 ‎2015-2016学年安徽省芜湖市芜湖县八年级（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、选择题：（每题3分，共30分）请将正确答案填写在下列方框内）‎ ‎1．下面有4个汽车标致图案，其中不是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎【考点】轴对称图形．‎ ‎【专题】几何图形问题．‎ ‎【分析】根据轴对称图形的概念结合4个汽车标志图案的形状求解．‎ ‎【解答】解：由轴对称图形的概念可知第1个，第2个，第3个都是轴对称图形．‎ 第4个不是轴对称图形，是中心对称图形．‎ 故选D．‎ ‎　‎ ‎2．如图，△ABD≌△ACE，若AB=6，AE=4，则CD的长度为（　　）‎ A．10 B．6 C．4 D．2‎ ‎【考点】全等三角形的性质．‎ ‎【分析】根据全等三角形的对应边相等可得AB=AC，AE=AD，再由CD=AC﹣AD即可求出其长度．‎ ‎【解答】解：∵△ABD≌△ACE，‎ ‎∴AB=AC=6，AE=AD=4，‎ ‎∴CD=AC﹣AD=6﹣4=2，‎ 故选D．‎ ‎　‎ ‎3．如图，△ABC与△A′B′C′关于直线l对称，则∠B的度数为（　　）‎ 第20页（共20页）‎ 鹤立文化辅导中心 A．30° B．50° C．90° D．100°‎ ‎【考点】轴对称的性质；三角形内角和定理．‎ ‎【分析】由已知条件，根据轴对称的性质可得∠C=∠C′=30°，利用三角形的内角和等于180°可求答案．‎ ‎【解答】解：∵△ABC与△A′B′C′关于直线l对称，‎ ‎∴∠A=∠A′=50°，∠C=∠C′=30°；‎ ‎∴∠B=180°﹣80°=100°．‎ 故选D．‎ ‎　‎ ‎4．已知等腰三角形的一边等于3，一边等于7，那么它的周长等于（　　）‎ A．13 B．13或17 C．17 D．14或17‎ ‎【考点】等腰三角形的性质；三角形三边关系．‎ ‎【专题】分类讨论．‎ ‎【分析】因为等腰三角形的两边分别为3和7，但没有明确哪是底边，哪是腰，所以有两种情况，需要分类讨论．‎ ‎【解答】解：当3为底时，其它两边都为7，7、7、3可以构成三角形，周长为17；‎ 当7为底时，其它两边都为3，因为3+3=6＜7，所以不能构成三角形，故舍去．‎ 所以它的周长等于17．‎ 故选C．‎ ‎　‎ ‎5．下列四个图形中，线段BE是△ABC的高的是（　　）‎ A． B． C． D．‎ ‎【考点】三角形的角平分线、中线和高．‎ ‎【分析】根据三角形高的画法知，过点B作AC边上的高，垂足为E，其中线段BE是△ABC的高，再结合图形进行判断．‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎【解答】解：线段BE是△ABC的高的图是选项D．‎ 故选D．‎ ‎　‎ ‎6．在△ABC内一点P满足PA=PB=PC，则点P一定是△ABC（　　）‎ A．三条角平分线的交点 B．三边垂直平分线的交点 C．三条高的交点 D．三条中线的交点 ‎【考点】线段垂直平分线的性质．‎ ‎【分析】由在△ABC内一点P满足PA=PB=PC，可判定点P在AB，BC，AC的垂直平分线上，则可求得答案．‎ ‎【解答】解：∵在△ABC内一点P满足PA=PB=PC，‎ ‎∴点P一定是△ABC三边垂直平分线的交点．‎ 故选B．‎ ‎　‎ ‎7．在△ABC和△FED中，如果∠A=∠F，∠B=∠E，要使这两个三角形全等，还需要的条件是（　　）‎ A．AB=DE B．BC=EF C．AB=FE D．∠C=∠D ‎【考点】全等三角形的判定．‎ ‎【分析】根据所给条件可知，应加一对对应边相等才可证明这两个三角形全等，AB和EF是对应边，因此应加AB=FE．‎ ‎【解答】解：A、加上AB=DE，不能证明这两个三角形全等，故此选项错误；‎ B、加上BC=EF，不能证明这两个三角形全等，故此选项错误；‎ C、加上AB=FE，可用ASA证明两个三角形全等，故此选项正确；‎ D、加上∠C=∠D，不能证明这两个三角形全等，故此选项错误；‎ 故选：C．‎ ‎　‎ ‎8．如图，已知AD平分∠BAC，AB=AC，则此图中全等三角形有（　　）‎ A．2对 B．3 对 C．4对 D．5对 ‎【考点】全等三角形的判定．‎ ‎【分析】根据SAS推出△ABD≌△ACD，求出∠B=∠C，BE=CF，根据全等三角形的判定推出△BDE≌△‎ 第20页（共20页）‎ 鹤立文化辅导中心 CDF，△AED≌△AFD，△AFB≌△AEC即可．‎ ‎【解答】解：全等三角形有：△ABD≌△ACD，△BDE≌△CDF，△AED≌△AFD，△AFB≌△AEC，共4对，‎ 故选C ‎　‎ ‎9．AD是△ABC的中线，DE=DF．下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【考点】全等三角形的判定与性质．‎ ‎【分析】根据三角形中线的定义可得BD=CD，然后利用“边角边”证明△BDF和△CDE全等，根据全等三角形对应边相等可得CE=BF，全等三角形对应角相等可得∠F=∠CED，再根据内错角相等，两直线平行可得BF∥CE，最后根据等底等高的三角形的面积相等判断出②正确．‎ ‎【解答】解：∵AD是△ABC的中线，‎ ‎∴BD=CD，‎ 在△BDF和△CDE中，‎ ‎，‎ ‎∴△BDF≌△CDE（SAS），故④正确 ‎∴CE=BF，∠F=∠CED，故①正确，‎ ‎∴BF∥CE，故③正确，‎ ‎∵BD=CD，点A到BD、CD的距离相等，‎ ‎∴△ABD和△ACD面积相等，故②正确，‎ 综上所述，正确的是①②③④．‎ 故答案为：①②③④．‎ ‎　‎ ‎10．已知AB=AC=BD，则∠1与∠2的关系是（　　）‎ 第20页（共20页）‎ 鹤立文化辅导中心 A．∠1=2∠2 B．2∠1+∠2=180° C．∠1+3∠2=180° D．3∠1﹣∠2=180°‎ ‎【考点】等腰三角形的性质．‎ ‎【分析】根据等腰三角形的性质和三角形内角和定理可得∠1和∠C之间的关系，再根据三角形外角的性质可得∠1和∠2之间的关系．‎ ‎【解答】解：∵AB=AC=BD，‎ ‎∴∠B=∠C=180°﹣2∠1，‎ ‎∴∠1﹣∠2=180°﹣2∠1，‎ ‎∴3∠1﹣∠2=180°．‎ 故选D．‎ ‎　‎ 二．填空题（3x8=24分）‎ ‎11．已知过一个多边形的某一顶点共可作2015条对角线，则这个多边形的边数是　2018　．‎ ‎【考点】多边形的对角线．‎ ‎【分析】根据从多边形的一个顶点可以作对角线的条数公式（n﹣3）求出边数即可得解．‎ ‎【解答】解：∵过一个多边形的某一顶点共可作2015条对角线，‎ 设这个多边形的边数是n，则 n﹣3=2015，‎ 解得n=2018．‎ 故答案为：2018．‎ ‎　‎ ‎12．如图，在△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD的周长为20cm，AE=5cm，则△ABC的周长是　30　cm．‎ ‎【考点】线段垂直平分线的性质．‎ ‎【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD，然后求出△ABD的周长=AB+BC，再根据三角形的周长公式列式计算即可得解．‎ ‎【解答】解：∵DE是AC的中垂线，‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎∴AD=CD，‎ ‎∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC，‎ 又∵AE=5cm，‎ ‎∴AC=2AE=2×5=10cm，‎ ‎∴△ABC的周长=20+10=30（cm）．‎ 故答案为：30．‎ ‎　‎ ‎13．将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为　75　度．‎ ‎【考点】三角形内角和定理；平行线的性质．‎ ‎【专题】计算题．‎ ‎【分析】根据三角形三内角之和等于180°求解．‎ ‎【解答】解：如图．‎ ‎∵∠3=60°，∠4=45°，‎ ‎∴∠1=∠5=180°﹣∠3﹣∠4=75°．‎ 故答案为：75．‎ ‎　‎ ‎14．已知等腰三角形的一个角的度数是50°，那么它的顶角的度数是　80°或50°　．‎ ‎【考点】等腰三角形的性质．‎ ‎【分析】等腰三角形一内角为50°，没说明是顶角还是底角，所以有两种情况．‎ ‎【解答】解：（1）当50°角为顶角，顶角度数即为50°；‎ ‎（2）当50°为底角时，顶角=180°﹣2×50°=80°．‎ 故答案为：80°或50°．‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎　‎ ‎15．点A（﹣2，a）和点B（b，﹣5）关于x轴对称，则a+b=　3　．‎ ‎【考点】关于x轴、y轴对称的点的坐标．‎ ‎【分析】先根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，﹣y）．求出a和b的值，然后求出a+b即可．‎ ‎【解答】解：∵A（﹣2，a）和点B（b，﹣5）关于x轴对称，‎ ‎∴a=5，b=﹣2，‎ ‎∴a+b=5﹣2=3．‎ 故答案为：3．‎ ‎　‎ ‎16．如图，已知在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于　5　．‎ ‎【考点】角平分线的性质．‎ ‎【分析】过E作EF⊥BC于点F，由角平分线的性质可求得EF=DE，则可求得△BCE的面积．‎ ‎【解答】解：‎ 过E作EF⊥BC于点F，‎ ‎∵CD是AB边上的高，BE平分∠ABC，‎ ‎∴BE=DE=5，‎ ‎∴S△BCE=BC•EF=×5×1=5，‎ 故答案为：5．‎ ‎　‎ ‎17．将等边三角形、正方形、正五边形按如图所示的位置摆放，如果∠1=41°，∠2=51°，那么∠3的度数等于　10°　．‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎【考点】多边形内角与外角；三角形内角和定理．‎ ‎【分析】利用360°减去等边三角形的一个内角的度数，减去正方形的一个内角的度数，减去正五边形的一个内角的度数，然后减去∠1和∠2即可求得．‎ ‎【解答】解：等边三角形的内角的度数是60°，正方形的内角度数是90°，正五边形的内角的度数是：（5﹣2）×180°=108°，‎ 则∠3=360°﹣60°﹣90°﹣108°﹣∠1﹣∠2=10°．‎ 故答案是：10°．‎ ‎　‎ ‎18．如图在△ABC中，BF、CF是角平分线，DE∥BC，分别交AB、AC于点D、E，DE经过点F．结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE； ③△ADE的周长=AB+AC；④BF=CF．其中正确的是　①②③　（填序号）‎ ‎【考点】等腰三角形的判定与性质；平行线的性质．‎ ‎【专题】推理填空题．‎ ‎【分析】由平行线得到角相等，由角平分线得角相等，根据平行线的性质及等腰三角形的判定和性质．‎ ‎【解答】解：∵DE∥BC，‎ ‎∴∠DFB=∠FBC，∠EFC=∠FCB，‎ ‎∵BF是∠ABC的平分线，CF是∠ACB的平分线，‎ ‎∴∠FBC=∠DFB，∠FCE=∠FCB，‎ ‎∵∠DBF=∠DFB，∠EFC=∠ECF，‎ ‎∴△DFB，△FEC都是等腰三角形．‎ ‎∴DF=DB，FE=EC，即有DE=DF+FE=DB+EC，‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC．‎ 综上所述，命题①②③正确．‎ 故答案为①②③．‎ ‎　‎ 三、解答题（本大题共有6小题，共46分）‎ ‎19．如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠EAD=5°，∠B=50°，求∠C的度数．‎ ‎【考点】三角形的角平分线、中线和高．‎ ‎【分析】根据直角三角形两锐角互余求出∠AED，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE，然后根据角平分线的定义求出∠BAC，再利用三角形的内角和定理列式计算即可得解．‎ ‎【解答】解：∵AD是BC边上的高，∠EAD=5°，‎ ‎∴∠AED=85°，‎ ‎∵∠B=50°，‎ ‎∴∠BAE=∠AED﹣∠B=85°﹣50°=35°，‎ ‎∵AE是∠BAC的角平分线，‎ ‎∴∠BAC=2∠BAE=70°，‎ ‎∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°．‎ ‎　‎ ‎20．如图，在△ABC中，D为BC的中点，DE⊥BC交∠BAC的平分线AE于E，EF⊥AB于F，EG⊥AC交AC延长线于G．求证：BF=CG．‎ ‎【考点】全等三角形的判定与性质；角平分线的性质；线段垂直平分线的性质．‎ ‎【专题】证明题．‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎【分析】连接EB、EC，利用已知条件证明Rt△BEF≌Rt△CEG，即可得到BF=CG．‎ ‎【解答】解：如图，连接BE、EC，‎ ‎∵ED⊥BC，‎ D为BC中点，‎ ‎∴BE=EC，‎ ‎∵EF⊥AB EG⊥AG，‎ 且AE平分∠FAG，‎ ‎∴FE=EG，‎ 在Rt△BFE和Rt△CGE中，‎ ‎，‎ ‎∴Rt△BFE≌Rt△CGE（HL），‎ ‎∴BF=CG．‎ ‎　‎ ‎21．（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；‎ ‎（2）直接写出A′，B′，C′三点的坐标：A′（　2，3　），B′（　3，1　），C′（　﹣1，﹣2　）．‎ ‎（3）计算△ABC的面积．‎ ‎【考点】作图-轴对称变换．‎ ‎【专题】计算题；作图题．‎ ‎【分析】（1）分别找出点A、B、C关于y轴的对应点A′、B′、C′，然后顺次连接即可得到△A′B′C′；‎ ‎（2）利用平面直角坐标系写出点的坐标即可；‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎（3）利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可．‎ ‎【解答】解：（1）如图；‎ ‎（2）A′（2，3），B′（3，1），C′（﹣1，﹣2）；‎ ‎（3）S△ABC=5×4﹣×1×2﹣×3×4﹣×5×3，‎ ‎=20﹣1﹣6﹣7.5，‎ ‎=5.5． ‎ ‎　‎ ‎22．如图，点D，E在△ABC的边BC上，连接AD，AE．①AB=AC；②AD=AE；③BD=CE以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：A：①②⇒③； B：①③⇒②； C：②③⇒①‎ 请选择一个真命题　①③②　 进行证明（先写出所选命题，然后证明）．‎ ‎【考点】命题与定理．‎ ‎【分析】根据全等三角形的判定定理和性质定理证明即可．‎ ‎【解答】已知：AB=AC，BD=CE，‎ 求证：AD=AE．‎ 证明：∵AB=AC，‎ ‎∴∠B=∠C，‎ 在△ABD和△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE，‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎∴AD=AE．‎ 故答案为：①③②．‎ ‎　‎ ‎23．如图，线段AC、BD交于点M，过B、D两点分别作AC的垂线段BF、DE，AB=CD ‎（1）若∠A=∠C，求证：FM=EM；‎ ‎（2）若FM=EM，则∠A=∠C．是真命题吗？（直接判断，不必证明）‎ ‎【考点】全等三角形的判定与性质．‎ ‎【分析】（1）由条件可先证明△ABF≌△CDE，可得BF=DE，再证明△BFM≌△DEM，可得到FM=EM；‎ ‎（2）由条件可先证明△BFM≌△DEM，可得BF=DE，再证明△ABF≌△DEM，可得∠A=∠C．‎ ‎【解答】（1）证明：∵BF⊥AC，DE⊥AC，‎ ‎∴∠AFB=∠CED，‎ 在△ABF和△CDE中，，‎ ‎∴△ABF≌△CDE（AAS），‎ ‎∴BF=DE，‎ 在△BFM和△DEM中，，‎ ‎∴△BFM≌△DEM（AAS），‎ ‎∴FM=EM；‎ ‎（2）解：真命题；理由如下：‎ ‎∵BF⊥AC，DE⊥AC，‎ ‎∴∠BFM=∠DEM=90°，‎ 在△BFM和△DEM中，，‎ ‎∴△BFM≌△DEM（ASA），‎ ‎∴BF=DE，‎ 在Rt△ABF和Rt△CDE中，‎ ‎∴Rt△ABF≌Rt△CDE（HL），‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎∴∠A=∠C．‎ ‎　‎ ‎24．如图，已知△ABC中，∠B=∠C，AB=8厘米，BC=6厘米，点D为AB的中点．如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t（秒）（0≤t≤3）．‎ ‎（1）用的代数式表示PC的长度；‎ ‎（2）若点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；‎ ‎（3）若点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？‎ ‎【考点】全等三角形的判定与性质；等腰三角形的性质．‎ ‎【专题】动点型．‎ ‎【分析】（1）先表示出BP，根据PC=BC﹣BP，可得出答案；‎ ‎（2）根据时间和速度分别求得两个三角形中的边的长，根据SAS判定两个三角形全等．‎ ‎（3）根据全等三角形应满足的条件探求边之间的关系，再根据路程=速度×时间公式，先求得点P运动的时间，再求得点Q的运动速度；‎ ‎【解答】解：（1）BP=2t，则PC=BC﹣BP=6﹣2t；‎ ‎（2））△BPD和△CQP全等 理由：∵t=1秒∴BP=CQ=2×1=2厘米，‎ ‎∴CP=BC﹣BP=6﹣2=4厘米，‎ ‎∵AB=8厘米，点D为AB的中点，‎ ‎∴BD=4厘米．‎ ‎∴PC=BD，‎ 在△BPD和△CQP中，‎ ‎，‎ ‎∴△BPD≌△CQP（SAS）；‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎（3）∵点P、Q的运动速度不相等，‎ ‎∴BP≠CQ 又∵△BPD≌△CPQ，∠B=∠C，‎ ‎∴BP=PC=3cm，CQ=BD=4cm，‎ ‎∴点P，点Q运动的时间t==秒，‎ ‎∴VQ===厘米/秒．‎ ‎　‎ 第20页（共20页）‎ 鹤立文化辅导中心 ‎2017年2月10日 第20页（共20页）‎