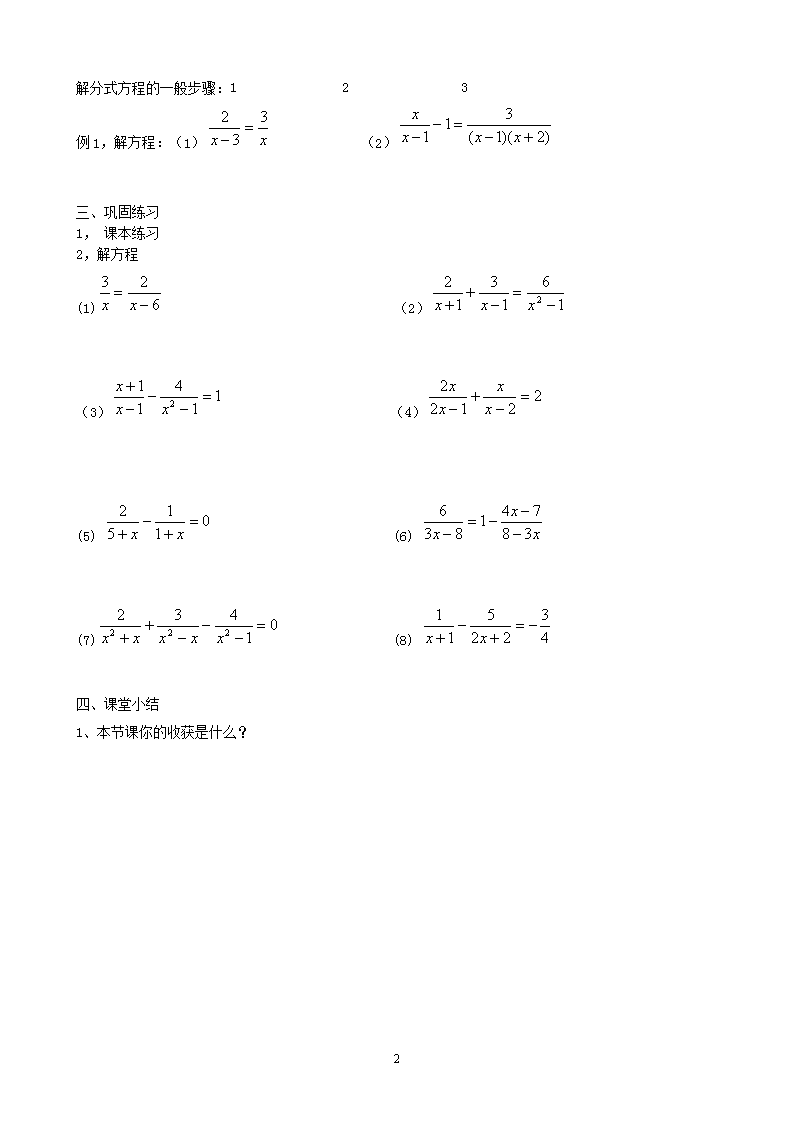分式方程导学案 2页

‎15．3． 分式方程（一）导学案 ‎【学习目标】‎ ‎1．了解分式方程的概念, 和产生增根的原因.‎ ‎2．掌握分式方程的解法，会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的增根.‎ 学习重点：会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的增根.‎ 学习难点：会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的增根.‎ 学习过程 一，复习引入 ‎1，回忆一元一次方程的解法，并且解方程 ‎2，一艘轮船在静水中的最大航速为‎20千米/时，它沿江以最大航速顺流航行‎100千米所用时间，与以最大航速逆流航行‎60千米所用时间相等，江水的流速为多少？‎ 分析：设江水的流速为v千米/时，根据“两次航行所用时间相同”这一等量关系，得到方程.‎ 二、探索新知 ‎1，分析方程的特征，然后概括出分式方程的概念；像这样__________________ ‎ ‎ 分式方程与整式方程的区别是_______________________________ _‎ 练习：下列方程中，哪些是分式方程？哪些是整式方程？‎ ‎(1) (2) (3) (4) ‎ ‎(5) (6) (7) (8) ‎ ‎ ‎ ‎2，解方程；‎ 方程两边同时乘以（20+v）（20-v）得 ‎ 解得：v= 检验： 将v= 代入分式方程，‎ ‎ 所以v= 是原分式方程的根. ‎ 解分式方程的基本思想： ‎ 在方程的两边同乘最简公分母，就可约去分母，化成整式方程，解分式方程的解的两种情况：‎ ‎①所得的根是原方程的根、②所得的根不是原方程的根 原方程的增根：在方程变形时，有时可能产生不适合原方程的根，这种根叫做原方程的增根 产生增根的原因：在把分式方程转化为整式方程时，分式的两边同时乘以了零 验根： 。‎ 2‎ 解分式方程的一般步骤：1 2 3 ‎ 例1，解方程：（1） （2）‎ 三、巩固练习 ‎ ‎1， 课本练习 ‎2，解方程 ‎(1) （2）‎ ‎（3） （4）‎ ‎(5) (6) ‎ ‎(7) (8) ‎ 四、课堂小结 ‎ ‎1、本节课你的收获是什么？ ‎ 2‎