八年级数学上册第四章一次函数4-4一次函数的应用第3课时两个一次函数图象的应用教学课件新版北师大版 28页

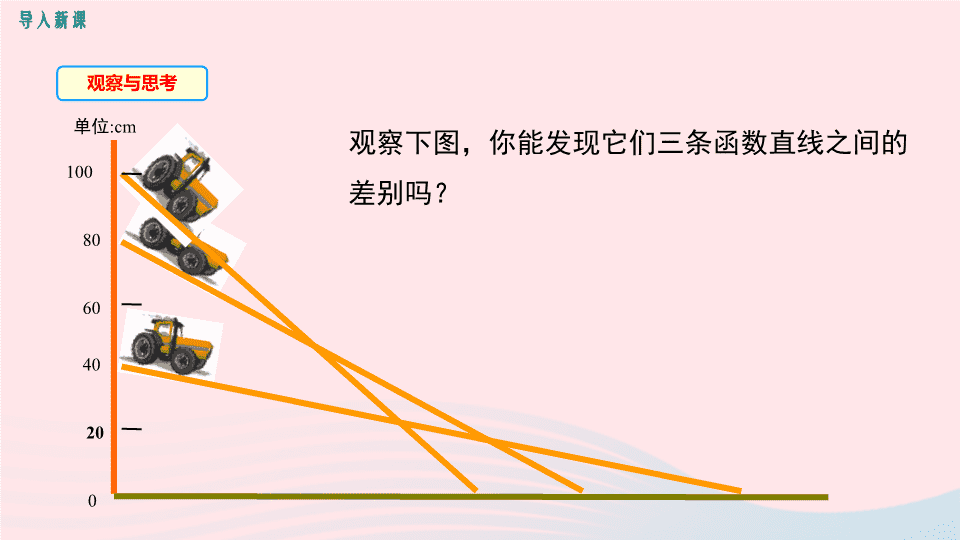
4.4 一次函数的应用 第四章 一次函数 第3课时 两个一次函数图象的应用 学习目标 1. 掌握两个一次函数图象的应用．（重点） 2. 能利用函数图象解决数学问题．（难点） 导入新课 观察与思考 20 0 40 60 80 100 单位 :cm 观察下图，你能发现它们三条函数直线之间的差别吗？ 讲授新课 两个一次函数的应用 一 x / 吨 y / 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 引例： l 1 反映了某公司产品的销售收入与销售量的关系，根据图意填空： l 1 当销售量为 2 吨时，销售收入＝ 　　 元， 2000 销售收入 x / 吨 y / 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 l 1 反映了公司产品的销售收入与销售量的关系 . 销售收入 l 1 对应的函数表达式是 　　　　　　　　 ， y =1000 x l 1 x / 吨 y / 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 l 2 反映了公司产品的销售成本与销售量的关系 销售成本 　　 l 2 对应的函数表达式是 　　　　　　　　 . y =500 x +2000 l 2 x / 吨 y / 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 l 2 当销售成本为 4500 元时，销售量＝ 　　 吨； 5 销售成本 x / 吨 y / 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 l 1 l 2 （ 1 ）当销售量为 6 吨时，销售收入＝ 　　　　 元， 　　 销售成本＝ 　　　 元， 利润＝ 　　　　 元 . 6000 5000 （ 2 ）当销售量为 　 　 时，销售收入等于销售成本 . 4 吨 销售收入 销售成本 1000 销售收入和销售成本 都是 4000 元 . x/ 吨 y/ 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 l 1 l 2 （ 3 ）当销售量 　　　　　 时，该公司赢利 ( 收入大于成本 ) ； 　　 当销售量 　　　　　 时，该公司亏损 ( 收入小于成本 ) ； 大于 4 吨 小于 4 吨 销售收入 销售成本 5 6 1 2 3 P 你还有什么发现？ 7 8 x/ 吨 y/ 元 O 1 2 3 4 5 6 1000 4000 5000 2000 3000 6000 销售成本 销售收入 l 1 ： y =1000 x 和 l 2 ： y =500 x +2000 中的 k 和 b 的实际意义各是什么？ l 2 l 1 想一想 k 的实际意义是表示销售每吨产品可收入或增加成本的量； b 的实际意义是表示变化的起始值 . 如 k 1 表示销售每吨产 品可收入 1000 元 b 2 表示销售成本从 2000 元开始逐步增加 b 1 表示收入从零到有 如 k 2 表示销售每吨产 品成本为 500 元 典例精析 例 1 ： 我边防局接到情报，近海处有一可疑船只 A 正向公海方向行驶，边防局迅速派出快艇 B 追赶（如图） . 海 岸 公 海 B A 下图中 l 1 ， l 2 分别表示两船相对于海岸的距离 S 与追赶时间 t 之间的关系 . 根据图象回答下列问题 （ 1 ）哪条线表示 B 到海岸的距离与追赶时间之间的关系？ 解：观察图象，得　　当 t ＝ 0 时， B 距海岸 0 海里，即 S ＝ 0 ， 故 l 1 表示 B 到海岸的距离与追赶时间之间的关系； 2 4 6 8 10 O 2 4 6 8 t / 分 s / 海里 l 1 l 2 Ｂ Ａ （ 2 ） A 、 B 哪个速度快？ t 从 0 增加到 10 时， l 2 的纵坐标增加了 2 ， l 1 的纵坐标增加了 5. 2 4 6 8 10 O 2 4 6 8 t / 分 s / 海里 l 1 l 2 Ｂ Ａ 即 10 分内， A 行驶了 2 海里， B 行驶了 5 海里， 所以 B 的速度快 7 5 当 t ＝ 15 时， l 1 上对应点在 l 2 上对应点的下方 这表明， 15 分钟时 B 尚未追上 A. 2 4 6 8 10 O 2 4 6 8 t / 分 s / 海里 l 1 l 2 Ｂ Ａ 12 14 （ 3 ） 15 分钟内 B 能否追上 A ？ 15 2 4 6 8 10 O 2 4 6 8 t / 分 s / 海里 l 1 l 2 Ｂ Ａ 12 14 （ 4 ）如果一直追下去，那么 B 能否追上 A ？ 　　如图延伸 l 1 、 l 2 相交于点 P. 因此，如果一直追下去，那么 B 一定能追上 A. P 2 4 6 8 10 O 2 4 6 8 t / 分 s / 海里 l 1 l 2 Ｂ Ａ 12 14 P （ 5 ）当 A 逃到离海岸 12 海里的公海时 ,B 将无法对其进行检查 . 照此速度， B 能否在 A 逃入公海前将其拦截？ 从图中可以看出， l 1 与 l 2 交点 P 的纵坐标小于 12 ， 这说明在 A 逃入公海前， 我边防快艇 B 能够追上 A. 10 k 1 表示快艇 B 的速度， k 2 表示可疑船只 A 的速度 . 可疑船只 A 的速度是 0.2 海里 / 分，快艇 B 的速度是 0.5 海里 / 分 . 2 4 6 8 10 O 2 4 6 8 t / 分 s / 海里 l 1 l 2 Ｂ Ａ 12 14 （ 6 ） l 1 与 l 2 对应的两个一次函数 y = k 1 x + b 1 与 y = k 2 x + b 2 中， k 1 ， k 2 的实际意义各是什么 ？可疑船只 A 与快艇 B 的速度各是多少？ 下图 l 1 , l 2 分别是龟兔赛跑中 s-t 函数图象 . （ 1 ）这一次是 　 米赛跑 . （ 2 ）表示兔子的图象是 . 100 l 2 练一练 s / 米 （ 3 ）当兔子到达终点时，乌龟距终点还有 　 米； l 1 l 2 1 2 3 4 5 O 100 20 120 40 60 80 t / 分 6 8 7 （ 4 ）乌龟要与兔子同时到达终点乌龟要先跑 米； （ 5 ）乌龟要先到达终点，至少要比兔子早跑 分钟； -1 12 9 10 11 -3 -2 40 4 -4 40 例 2 ： 已知一次函数 y ＝ x ＋ a 和 y ＝－ x ＋ b 的图象都经过点 A( － 4 ， 0) ，且与 y 轴分别交于 B 、 C 两点，求 △ABC 的面积． 解： ∵y ＝ x ＋ a 与 y ＝－ x ＋ b 的 图象都过点 A( － 4 ， 0) ， ∴ ×( － 4) ＋ a ＝ 0 ，－ ×( － 4) ＋ b ＝ 0. ∴a ＝ 6 ， b ＝－ 2. ∴ 两个一次函数分别是 y ＝ x ＋ 6 和 y ＝－ x － 2. y ＝ x ＋ 6 与 y 轴交于点 B ，则 y ＝ ×0 ＋ 6 ＝ 6 ， ∴B(0 ， 6) ； y ＝－ x － 2 与 y 轴交于点 C ，则 y ＝－ 2 ， ∴C(0 ，－ 2) ． 如图所示， S △ABC ＝ BC·AO ＝ ×4×(6 ＋ 2) ＝ 16. 方法总结： 解此类题要先求得顶点的坐标，即两个一次函数的交点和它们分别与 x 轴、 y 轴交点的坐标． 当堂练习 1. 如图，射线 OA 、 BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中 s 、 t 分别表示行驶距离和时间，则这两人骑自行车的速度相差 km/h． 解析：根据图象可得出：甲的速度为 120÷5=24 （ km/h ） ， 乙的速度为 ( 120﹣4) ÷5=23.2 （ km/h ） ， 速度差为 24﹣23.2=0.8 （ km/h ）， 0.8 B 解析：设小明的速度为 a 米 / 秒，小刚的速度为 b 米 / 秒，由题意得 1600+100 a =1400+100 b , 1600+300 a =1400+200 b , 解得 a =2, b =4. 故这次越野跑的全程为 1600+300×2=220 米． 2. 一次越野跑中，当小明跑了1600米时，小刚跑了1400米，小明、小刚所跑的路程 y （米）与时间t（秒）之间的函数关系如图，则这次越野跑的全程为 米． 2200 3. 小亮和小明周六到距学校 24km 的滨湖湿地公园春游，小亮 8 ： 00 从学校出发，骑自行车去湿地公园，小明 8 ： 30 从学校出发，乘车沿相同路线去滨湖湿地公园，在同一直角坐标系中，小亮和小明的行进路程 S（km） 与时间 t （时）的函数图象如图所示．根据图象得到结论，其中错误的是（　　） A ． 小亮骑自行车的平均速度是 12km/h B ． 小明比小亮提前0.5小时到达滨湖湿地公园 C ．小明在距学校 12km 处追上小亮 D ． 9：30小明与小亮相距 4km D 解 ： A. 根据函数图象小亮去滨湖湿地公园所用时间为 10 ﹣ 8=2 小时， ∴ 小亮骑自行车的平均速度为： 24 ÷ 2=12 （ km/h ），故正确； B . 由图象可得，小明到滨湖湿地公园对应的时间 t=9.5 ，小亮到滨湖湿地公园对应的时间 t=10 ， 10 ﹣ 9.5=0.5 （小时） ， ∴ 小明比小亮提前0.5小时到达滨湖湿地公园，故正确； C . 由图象可知，当t=9时，小明追上小亮，此时小亮离开学校的时间为9﹣8=1小时， ∴ 小亮走的路程为 ： 1 × 12=12km ， ∴ 小明在距学校12km出追上小亮，故正确 ； D . 由图象可知，当t=9.5时，小明的路程为24km，小亮的路程 为 12 × （ 9.5 ﹣ 8 ） =18km ， 此时小明与小亮相距24﹣18=6km，故错误；故选： D ． 4. 在一次蜡烛燃烧试验中，甲、乙两根蜡烛燃烧时剩余部分的高度 y （厘米）与燃烧时间 x （时）之间的关系如图所示，请根据图象所提供的信息解答下列问题： （ 1 ）甲、乙两根蜡烛燃烧 前的高度分别是 ， 从点燃到燃尽所用的时间 分别是 . 30 厘米 、 25 厘米 2 时、 2.5 时 （ 2 ）分别求甲、乙两根蜡烛燃烧时 y 与 x 之间的函数关系式； （ 3 ）燃烧多长时间时，甲、乙两根蜡烛的高度相等（不考虑都燃尽时的情况）？ 在什么时间段内，甲蜡烛比乙蜡烛高？ 在什么时间段内，甲蜡烛比乙蜡烛低？ y 甲 =-15 x +30 y 乙 =-10 x +25 x =1 x >1 x <1 两个一次函数的应用 方案选择问题 课堂小结 实际生活中的问题