北京课改版数学八上第十二章《三角形》单元测试 16页

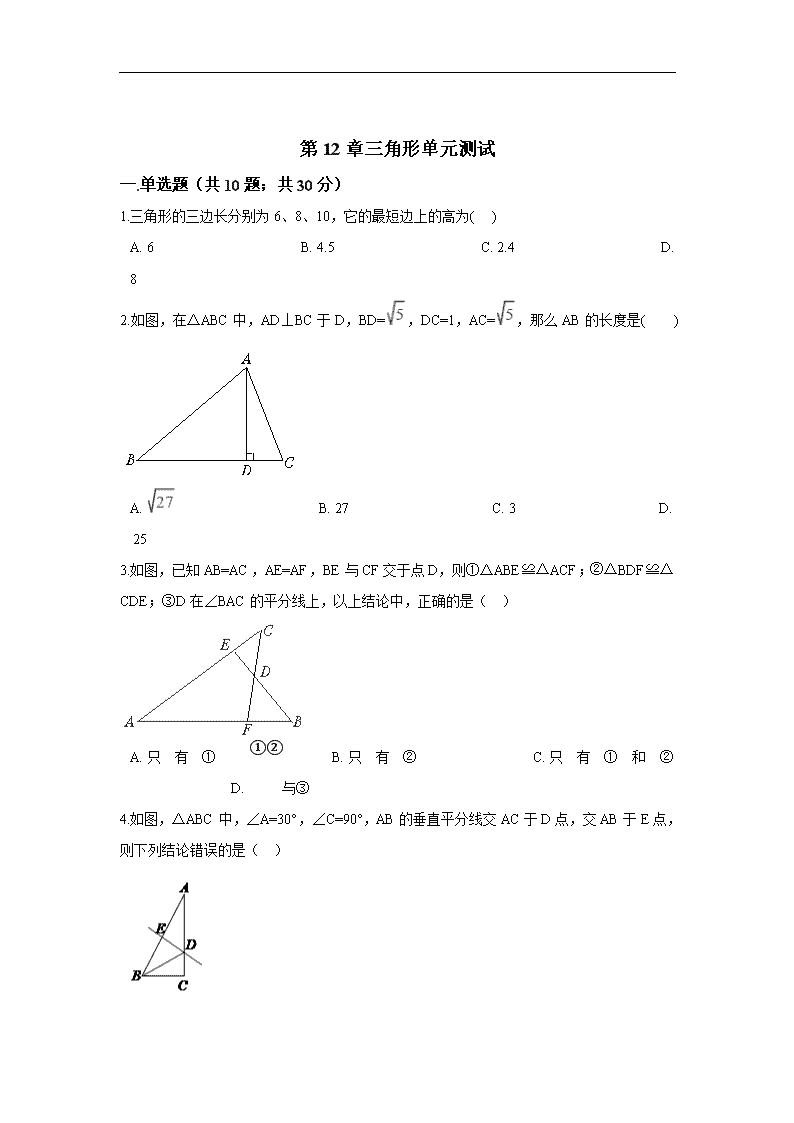
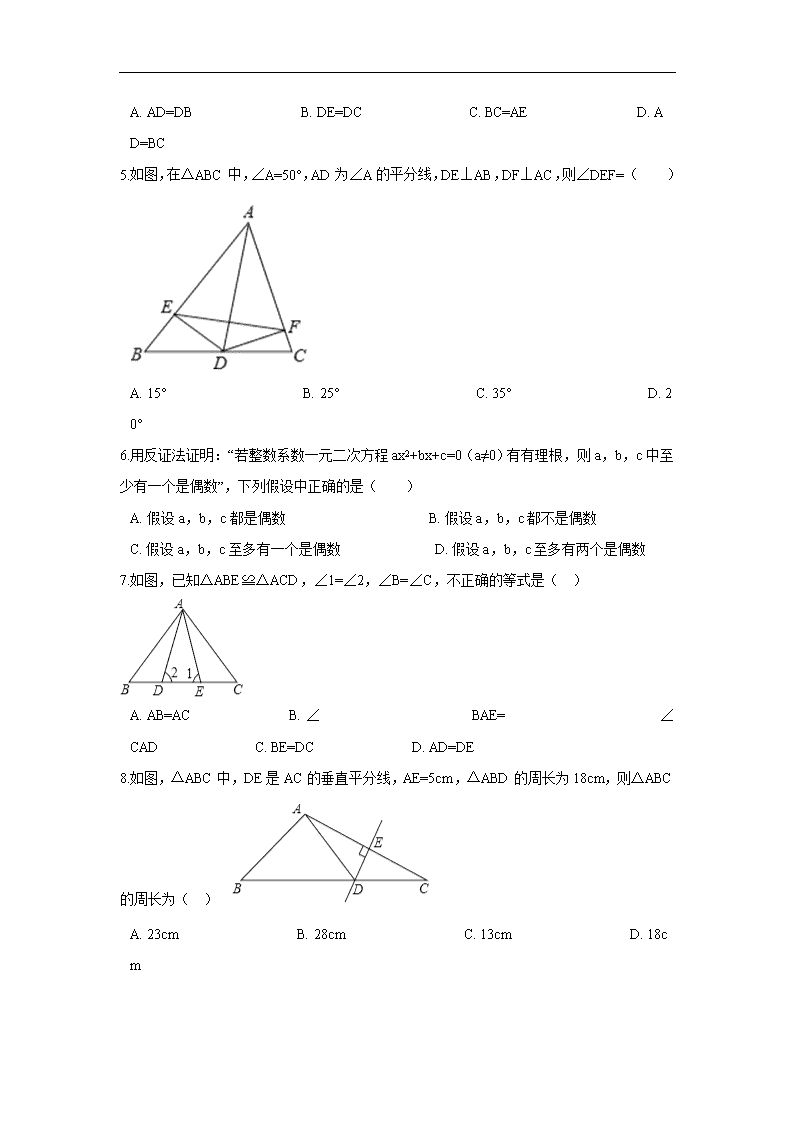
第 12 章三角形单元测试 一.单选题（共 10 题；共 30 分） 1.三角形的三边长分别为 6、8、10，它的最短边上的高为( ) A. 6 B. 4.5 C. 2.4 D. 8 2.如图，在△ABC 中，AD⊥BC 于 D，BD= ，DC=1，AC= ，那么 AB 的长度是( ) A. B. 27 C. 3 D. 25 3.如图，已知 AB=AC，AE=AF，BE 与 CF 交于点 D，则①△ABE≌△ACF；②△BDF≌△ CDE；③D 在∠BAC 的平分线上，以上结论中，正确的是（ ） A. 只 有 ① B. 只 有 ② C. 只 有 ① 和 ② D. ①②与③ 4.如图，△ABC 中，∠A=30°，∠C=90°，AB 的垂直平分线交 AC 于 D 点，交 AB 于 E 点， 则下列结论错误的是（ ） A. AD=DB B. DE=DC C. BC=AE D. A D=BC 5.如图，在△ABC 中，∠A=50°，AD 为∠A 的平分线，DE⊥AB，DF⊥AC，则∠DEF= （ ） A. 15° B. 25° C. 35° D. 2 0° 6.用反证法证明：“若整数系数一元二次方程 ax2+bx+c=0（a≠0）有有理根，则 a，b，c 中至 少有一个是偶数”，下列假设中正确的是（ ） A. 假设 a，b，c 都是偶数 B. 假设 a，b，c 都不是偶数 C. 假设 a，b，c 至多有一个是偶数 D. 假设 a，b，c 至多有两个是偶数 7.如图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是（ ） A. AB=AC B. ∠ BAE= ∠ CAD C. BE=DC D. AD=DE 8.如图，△ABC 中，DE 是 AC 的垂直平分线，AE=5cm，△ABD 的周长为 18cm，则△ABC 的周长为（ ） A. 23cm B. 28cm C. 13cm D. 18c m 9.如图，已知 D 为 BC 上一点，∠B=∠1，∠BAC=78°，则∠2=（ ） A. 78° B. 80° C. 50° D. 6 0° 10.下列说法正确的是（ ） A. 面积相等的两个三角形全等 B. 周长相等的两个三角形全等 C. 形状相同的两个三角形全等 D. 成轴对称的两个三角形全等 二.填空题（共 8 题；共 27 分） 11.空调安装在墙上时，一般都会象如图所示的方法固定在墙上，这种方法应用的数学知识 是________ ． 12.电工师傅在安好电线杆后，为了防止电线杆倾倒，常常按图所示引两条拉线，这样做的 数学道理是________ ． 13.有一块直角三角形绿地，量得两直角边长分别为 3m，4m，现在要将绿地扩充成等腰三 角形，且扩充时只能延长两条直角边中的一条，则扩充后等腰三角形绿地的面积为 ________m2 ． 14.已知在△ABC 中，AB=13cm，AC=15cm，高 AD=12cm．则△ABC 的周长为________． 15.已知等腰三角形的一个内角是 30°，那么这个等腰三角形顶角的度数是________． 16.如图，七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=________． 17.若三角形的一个外角等于和它相邻的内角，则这个三角形一定是________三角形；若三 角形的一个外角小于和它相邻的内角，则这个三角形一定是________三角形． 18.在△ABC 中，∠A=40°，∠B=80°，则∠C 的度数为________． 三.解答题（共 6 题；共 42 分） 19.已知 AB=AC，AE 平分∠DAC，那么 AE∥BC 吗？为什么？ 20.在直角三角形中，有一个锐角是另一个锐角的 4 倍，求这个直角三角形各个角的度数． 21.如图，在△ABC 中，AB=AC，点 D 在 AC 上，且 BD=BC=AD，求△ABC 各角的度数． ​ 22.如图，在△ABC 中，AC=8，BC=6，在△ABE 中，DE 是 AB 边上的高，且 DE=7，△ABE 的面积为 35，求∠C 的度数． 23.已知：如图，△ABC 中，BD，CD 是高，G、F 分别是 BC，DE 的中点．试判断 FG 与 DE 的位置关系，并加以证明． 24.如图 ，在四 边形 ABCD 中， ∠B= ∠D=90° ，∠ A=60°， BC=2 ， CD=1 ，求 AD 的 长． 答案解析 一.单选题 1.【答案】D 【考点】勾股定理的应用 【解析】 【分析】根据已知先根据勾股定理的逆定理判定其形状，再根据高的定义即可求解． 【解答】∵三角形的三边长分别为 6，8，10，符合勾股定理的逆定理 62+82=102 ， ∴此三角形为直角三角形，则 6 为直角三角形的最短边，并且是直角边， 那么这个三角形的最短边上的高为 8． 故选：D． 【点评】本题考查了勾股定理的逆定理，解答此题的关键是先判断出三角形的形状，再根据 高的定义解答 2.【答案】C 【考点】勾股定理 【解析】【分析】根据 AC，DC 解直角△ACD，可以求得 AD，根据求得的 AD 和 BD 解直角△ABD，可以 计算 AB． 【解答】∵△ACD 为直角三角形， ∴AC2=AD2+DC2， ∴AD= =2， ∵△ABD 为直角三角形， ∴AB2=AD2+BD2， ∴AB= =3， 故选 C． 【点评】本题考查了直角三角形中勾股定理的灵活运用，根据两直角边求斜边，根据斜边和一条直角边求 另一条直角边。 3.【答案】D 【考点】全等三角形的判定与性质 【解析】【分析】由 AB=AC，AE=AF，公共角∠A 可证得△ABE≌△ACF，即可得到∠B= ∠C，再结合对顶角相等可得△BDF≌△CDE，得到 CD=BD，从而证得△ACD≌△ABD. ∵AB=AC，AE=AF，∠A=∠A ∴△ABE≌△ACF ∴∠B=∠C ∵AB=AC，AE=AF ∴CE=BF ∵∠CDE=∠BDF ∴△BDF≌△CDE ∴CD=BD ∵AB=AC，∠B=∠C ∴△ACD≌△ABD ∴D 在∠BAC 的平分线上 故选 D. 【点评】全等三角形的判定与性质的应用贯穿于整个初中学习，是平面图形中极为重要的知 识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注。 4.【答案】D 【考点】线段垂直平分线的性质 【解析】【分析】∵DE 是线段 AB 的垂直平分线 ∴AD=BD，AE=BE 易证△BDE≌△BDC ∴DE=DC，BE=BC ∴BC=AE 因此 A、B、C 选项正确，D 错误； 故选 D. 5.【答案】B 【考点】角平分线的性质 【解析】【解答】解：∵AD 为∠A 的平分线，DE⊥AB，DF⊥AC， ∴∠AED=∠AFD=90°，DE=DF， ∵∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=360°﹣90°﹣90°﹣50°=130°， ∵DE=DF， ∴∠DEF=∠DFE= （180°﹣∠EDF）= ×（180°﹣130°）=25°， 故选 B． 【分析】根据角平分线性质得出 DE=DF，求出∠AAED=∠AFD=90°，求出∠EDF，根据等 腰三角形性质和三角形的内角和定理求出即可． 6.【答案】B 【考点】反证法 【解析】【解答】解：用反证法法证明数学命题时，应先假设要证的命题的反面成立，即要 证的命题的否定成立， 而命题：“若整数系数一元二次方程 ax2+bx+c=0（a≠0）有有理根，则 a，b，c 中至少有一个 是偶数”的否定为：“假设 a，b，c 都不是偶数”， 故选：B． 【分析】用反证法法证明数学命题时，应先假设命题的反面成立，求出要证的命题的否定， 即为所求． 7.【答案】D 【考点】全等三角形的性质 【解析】【解答】解：∵△ABE≌△ACD，∠1=∠2，∠B=∠C， ∴AB=AC，∠BAE=∠CAD，BE=DC，AD=AE， 故 A、B、C 正确； AD 的对应边是 AE 而非 DE，所以 D 错误． 故选 D． 【分析】根据全等三角形的性质，全等三角形的对应边相等，全等三角形的对应角相等，即 可进行判断． 8.【答案】B 【考点】线段垂直平分线的性质 【解析】【解答】解：∵DE 是 AC 的中垂线， ∴AD=CD， ∴△ABD 的周长=AB+BD+AD=AB+BD+CD=AB+BC， 又∵AE=5cm， ∴AC=2AE=2×5=10cm， ∴△ABC 的周长=18+10=28cm， 故选 B． 【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得 AD=CD，然后求出△ ABD 的周长=AB+BC，再根据三角形的周长公式列式计算即可得解 9.【答案】A 【考点】三角形内角和定理，三角形的外角性质 【解析】【解答】解：∵∠2=∠B+∠BAD，∠BAC=∠1+∠BAD， 又∵∠B=∠1， ∴∠2=∠BAC， ∵∠BAC=78°， ∴∠2=78°． 故选 A． 【分析】由图知，∠2=∠B+∠BAD，∠BAC=∠1+∠BAD，根据已知，可以得到∠2=∠BAC， 进而可以求出∠2． 10.【答案】D 【考点】全等三角形的判定 【解析】【解答】解：A．面积相等的两个三角形不一定全等，错误； B．周长相等的两个 三角形不一定全等，错误； C．形状相同的两个三角形不一定全等，错误； D．成轴对称的两个三角形全等，正确； 故选 D． 【分析】根据三角形全等的判定定理进行解答即可． 二.填空题 11.【答案】三角形的稳定性 【考点】三角形的稳定性 【解析】【解答】解：这种方法应用的数学知识是：三角形的稳定性． 【分析】钉在墙上的方法是构造三角形，因而应用了三角形的稳定性． 12.【答案】三角形的稳定性 【考点】三角形的稳定性 【解析】【解答】解：结合图形，为了防止电线杆倾倒，常常按图所示引两条拉线，两条拉 线与地面就构成了三角形，所以这样做根据的数学道理是三角形的稳定性． 故答案是：三角形的稳定性． 【分析】根据三角形的三边一旦确定，则形状大小完全确定，即三角形的稳定性． 13.【答案】8 或 10 或 12 或 或 【考点】勾股定理的应用 【解析】【解答】解：①如图 1： 当 BC=CD=3m 时； 由于 AC⊥BD，则 AB=AD=5m； 此时等腰三角形绿地的面积： ×6×4=12（m2）； ②如图 2： 当 AC=CD=4m 时； ∵AC⊥CB， 此时等腰三角形绿地的面积： ×4×4=8（m2）； ③图 3： 当 AD=BD 时，设 AD=BD=xm； Rt△ACD 中，BD=xm，CD=（x﹣3）m； 由勾股定理，得 AD2=DC2+CA2 ， 即（x﹣3）2+42=x2 ， 解得 x= ； 此时等腰三角形绿地的面积： ×BD×AC= × ×4= （m2）． ④如图 4， 延长 BC 到 D 使 BD 等于 5m， 此时 AB=BD=5m， 故 CD=2m， •BD•AC= ×5×4=10（m2）． ⑤如图 5， 延长 AC 到 D 使 AD 等于 5m， 此时 AB=AD=5m， 故 BC=3m， •BC•AD= ×5×3= （m2）． 故答案为：8 或 10 或 12 或 或 ． 【分析】由于扩充所得的等腰三角形腰和底不确定，若设扩充所得的三角形是△ABD，则 应分为①BC=CD，②AC=CD，③AD=BD，④AB=BD，⑤AD=AB，5 种情况进行讨论． 14.【答案】42cm 或 32cm 【考点】勾股定理 【解析】【解答】32cm 或 42cm 解：分两种情况说明：（1）当△ABC 为锐角三角形时，在 Rt△ABD 中， BD= = =5， 在 Rt△ACD 中， CD= = =9， ∴BC=5+9=14， ∴△ABC 的周长为：15+13+14=42（cm）；（2）当△ABC 为钝角三角形时， BC=BD﹣CD=9﹣5=4． ∴△ABC 的周长为：15+13+4=32（cm）； 故答案为：42cm 或 32cm． 【分析】分两种情况进行讨论：（1）当△ABC 为锐角三角形时，在 Rt△ABD 和 Rt△ACD 中，运用勾股定理可将 BD 和 CD 的长求出，两者相加即为 BC 的长，从而可将△ABC 的周 长求出；（2）当△ABC 为钝角三角形时，求出 BC 的长，从而可将△ABC 的周长求出． 15.【答案】30°或 120° 【考点】等腰三角形的性质 【解析】【解答】解：当 30°是等腰三角形的顶角时，顶角就是 30°； 当 30°是等腰三角形 的底角时，则顶角是 180°﹣30°×2=120°． 则该等腰三角形的顶角是 30°或 120°． 故填 30°或 120°． 【分析】分情况讨论：当 30°是等腰三角形的顶角时或当 30°是等腰三角形的底角时．再结 合三角形的内角和是 180°进行计算． 16.【答案】180° 【考点】三角形内角和定理，三角形的外角性质 【解析】【解答】解：由三角形的外角性质得，∠1=∠B+∠F+∠C+∠G， ∠2=∠A+∠D， 由三角形的内角和定理得，∠1+∠2+∠E=180°， 所以，∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°． 故答案为：180°． 【分析】根据三角形的一个外角等于与它不相邻的两个内角的和解答即可． 17.【答案】直角；钝角 【考点】三角形的外角性质 【解析】【解答】解：根据题意，与这个外角相邻的内角等于 180°÷2=90°， 则这个三角形 是直角三角形． 由三角形的一个外角小于和它相邻的内角， 则这个三角形是钝角， 故答案为直角，钝角． 【分析】根据三角形的一个外角等于和它不相邻的两个内角的和与三角形的内角和等于 180° 可以判断出三角形的形状． 18.【答案】60° 【考点】三角形内角和定理 【解析】【解答】解：∵三角形的内角和是 180° 又∠A=40°，∠B=80° ∴∠C=180°﹣∠A﹣∠B =180°﹣40°﹣80° =60°． 故答案为：60°． 【分析】在△ABC 中，根据三角形内角和是 180 度来求∠C 的度数． 三.解答题 19.【答案】解：AE∥BC． ∵AB=AC， ∴∠B=∠C， 由三角形的外角性质得，∠DAC=∠B+∠C=2∠B， ∵AE 平分∠DAC， ∴∠DAC=2∠DAE， ∴∠B=∠DAE， ∴AE∥BC． 【考点】等腰三角形的性质 【解析】【分析】根据等边对等角可得∠B=∠C，再利用三角形的一个外角等于与它不相邻 的两个内角的和求出∠DAC=2∠B，根据角平分线的定义可得∠DAC=2∠DAE，然后求出 ∠B=∠DAE，最后根据同位角相等，两直线平行证明即可． 20.【答案】解：设设一个锐角为 x 度，则另一个锐角为 4x 度， 那么根据三角形内角和定理：三角形内角之和为 180°， 所以 x+4x+90°=180°， x=18°，4x=72°， 答：三角分别为 18°，72°，90°． 【考点】直角三角形全等的判定 【解析】【分析】设一个锐角为 x 度，则另一个锐角为 4x 度，然后根据三角形的内角和定理 列方程求解即可． 21.【答案】解：设∠A=x． ∵AD=BD， ∴∠ABD=∠A=x； ∵BD=BC， ∴∠BCD=∠BDC=∠ABD+∠A=2x； ∵AB=AC， ∴∠ABC=∠BCD=2x， ∴∠DBC=x； ∵x+2x+2x=180°， ∴x=36°， ∴∠A=36°， ∠ABC=∠ACB=72°． 【考点】等腰三角形的性质 【解析】【分析】设∠A=x，利用等腰三角形的性质和三角形内角和定理即可求得各角的度 数． 22.【答案】解：∵DE=7，S△ABE=12DE•AB=35， ∴AB=10 ∵AC=8，BC=6，62+82=102 ， ∴AC2+BC2=AB2 由勾股定理逆定理得∠C=90°． 【考点】勾股定理 【解析】【分析】由 S△ABE=35，求得 AB=10，根据勾股定理的逆定理得出△ABC 为直角三 角形，从而得到∠C 的度数． 23.【答案】解：FG⊥DE． 理由如下：如图，连接 DG、FG， ∵BD、CE 分别是△ABC 的 AC、BC 边上的高，点 G 是 BC 的中点， ∴DG=EG= BC， ∵点 F 是 DE 的中点， ∴FG⊥DE． 【考点】等腰三角形的判定与性质，直角三角形斜边上的中线 【解析】【分析】连接 DG、FG，根据直角三角形斜边上的中线等于斜边的一半可得 DG=EG= 12 BC，再根据等腰三角形三线合一的证明即可． 24.【答案】解：分别延长 AD、DC 交于点 E， 在 Rt△ABE 中，∵∠A=60°， ∴∠E=30°， 在 Rt△CBE 中，∵∠E=30°，BC=2， ∴EC=4， ∴DE=4+1=5， 在 Rt△ABE 中，∠E=30°， AE=2AD， AE2=AD2+DE2 ， 4AD2=AD2+52 ， 解得：AD= ． 【考点】勾股定理 【解析】【分析】延长 AD，DC 交于点 E，可得直角三角形 ABE，易得 CE 长，在 Rt△CBE 中，利用 30°的三角函数可得 EC，DE 的长，进而利用勾股定理可得 AD 长．