人教版九年级上册数学 第22章 二次函数 综合练习（含答案） 10页

第22章 二次函数 综合练习 ‎ 一 选择题：‎ ‎1.已知抛物线y=ax2＋bx＋c(a＞0)过(-2，0)，(2，3)两点，那么抛物线的对称轴( )‎ ‎ A.只能是x=-1  B.可能是y轴 ‎ C.可能在y轴右侧且在直线x=2的左侧  D.可能在y轴左侧且在直线x=-2的右侧 ‎2.已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值y<0,那么下列结论中正确的是（　 ） ‎ ‎ A.m﹣1的函数值小于0    B.m﹣1的函数值大于0      ‎ ‎ C.m﹣1的函数值等于0         D.m﹣1的函数值与0的大小关系不确定   ‎ ‎3.已知二次函数y=2x2+4x﹣5，设自变量的值分别为x1、x2、x3，且﹣1＜x1＜x2＜x3，则对应的函数值y1、y2、y3的大小关系为（　 　）‎ ‎ A.y1＞y2＞y3 B.y1＜y2＜y‎3 C.y2＜y3＜y1 D.y2＞y3＞y1‎ ‎4.已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：‎ x ‎…‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y ‎…‎ ‎5‎ ‎2‎ ‎1‎ ‎2‎ ‎…‎ 点A（x1，y1）、B（x2，y2）在函数的图象上,则当0＜x1＜1，2＜x2＜3时,y1与y2大小关系正确的是（　　）‎ ‎ A.y1≥y2       B.y1＞y2       C.y1＜y2       D.y1≤y2‎ ‎5.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论：①abc>0；②﹣b0；‎ ‎ ④b2﹣4ac>0.其中正确的结论有(     )‎ ‎ A.1个  B.2个    C.3个   D.4个 ‎ ‎ ‎ 第5题图 第6题图 ‎6.已知顶点为(-3，-6)的抛物线经过点(-1，-4)，下列结论中错误的是（     ）‎ ‎ A. B.若点(-2，)，(-5，) 在抛物线上，则 ‎ C. D. 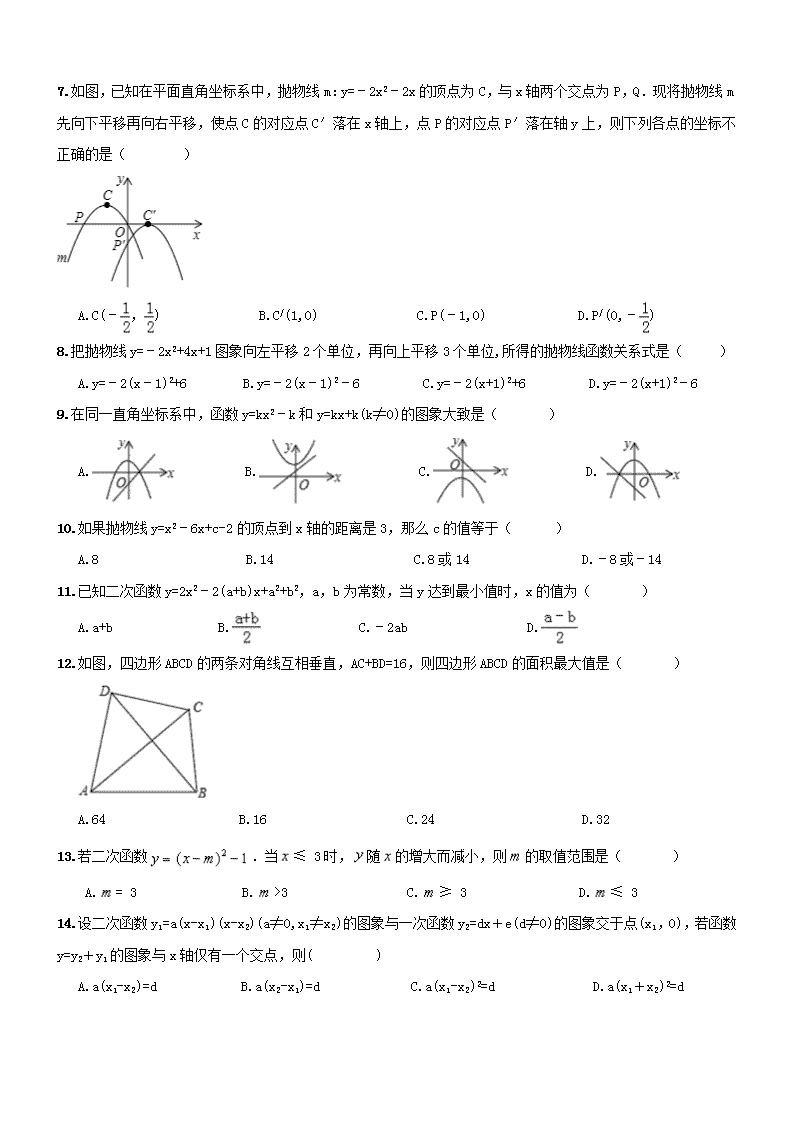关于的一元二次方程的两根为-5和-1‎ ‎7.如图，已知在平面直角坐标系中，抛物线m：y=﹣2x2﹣2x的顶点为C，与x轴两个交点为P，Q．现将抛物线m先向下平移再向右平移，使点C的对应点C′落在x轴上，点P的对应点P′落在轴y上，则下列各点的坐标不正确的是（　 　）‎ ‎　 A.C(﹣，) B.C/(1,0) C.P(﹣1,0) D.P/(0,﹣)‎ ‎8.把抛物线y=﹣2x2+4x+1图象向左平移2个单位，再向上平移3个单位,所得的抛物线函数关系式是（　 　）‎ ‎ A.y=﹣2(x﹣1)2+6 B.y=﹣2(x﹣1)2﹣6 C.y=﹣2(x+1)2+6  D.y=﹣2(x+1)2﹣6‎ ‎9.在同一直角坐标系中，函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是（　 　）‎ ‎ A. B. C.  D.‎ ‎10.如果抛物线y=x2﹣6x+c-2的顶点到x轴的距离是3，那么c的值等于（ 　　）‎ ‎ A.8    B.14    C.8或14     D.﹣8或﹣14‎ ‎11.已知二次函数y=2x2﹣2(a+b)x+a2+b2，a，b为常数，当y达到最小值时，x的值为（　 　）‎ ‎ A.a+b  B. 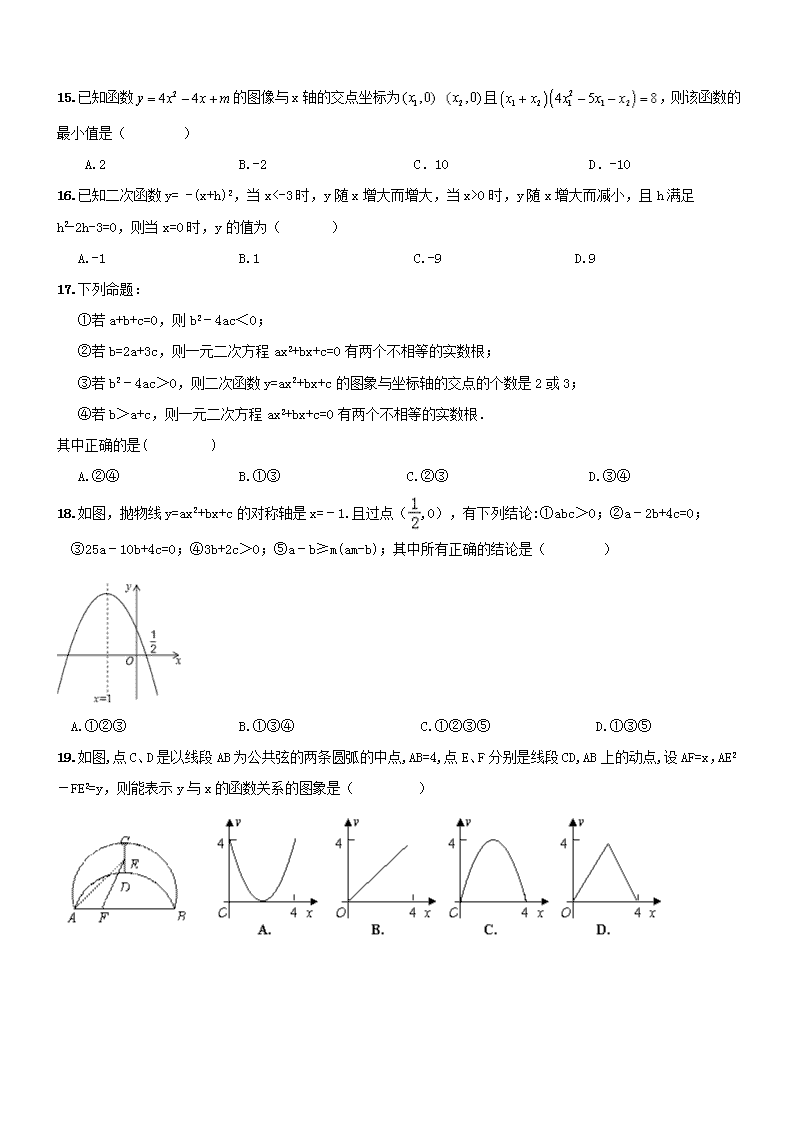C.﹣2ab    D.‎ ‎12.如图，四边形ABCD的两条对角线互相垂直，AC+BD=16，则四边形ABCD的面积最大值是（　 　）‎ ‎ ‎ ‎ A.64   B.16    C.24   D.32‎ ‎13.若二次函数．当≤ 3时，随的增大而减小，则的取值范围是（   ）‎ ‎  A.= 3        B.>3         C.≥ 3        D.≤ 3  ‎ ‎14.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx＋e(d≠0)的图象交于点(x1，0)，若函数y=y2＋y1的图象与x轴仅有一个交点，则(  )‎ ‎ A.a(x1-x2)=d　　　　   B.a(x2-x1)=d C.a(x1-x2)2=d　　　     D.a(x1＋x2)2=d ‎15.已知函数的图像与x轴的交点坐标为 且，则该函数的最小值是（　　 　）‎ ‎ A.2          B.-2           C．10           D．-10‎ ‎16.已知二次函数y= -(x+h)2，当x<-3时，y随x增大而增大，当x>0时，y随x增大而减小，且h满足h2-2h-3=0，则当x=0时，y的值为（    ）‎ ‎ A.-1         B.1         C.-9          D.9‎ ‎17.下列命题：‎ ‎ ①若a+b+c=0，则b2﹣4ac＜0；‎ ‎ ②若b=2a+3c，则一元二次方程ax2+bx+c=0有两个不相等的实数根；‎ ‎ ③若b2﹣4ac＞0，则二次函数y=ax2+bx+c的图象与坐标轴的交点的个数是2或3；‎ ‎ ④若b＞a+c，则一元二次方程ax2+bx+c=0有两个不相等的实数根．‎ 其中正确的是(     )‎ ‎ A.②④ B.①③  C.②③ D.③④‎ ‎18.如图，抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点（,0），有下列结论:①abc＞0；②a﹣2b+4c=0；‎ ‎ ③25a﹣10b+4c=0；④3b+2c＞0；⑤a﹣b≥m(am-b)；其中所有正确的结论是（　 　）‎ ‎ A.①②③   B.①③④   C.①②③⑤ D.①③⑤‎ ‎19.如图,点C、D是以线段AB为公共弦的两条圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点,设AF=x，AE2－FE2=y，则能表示y与x的函数关系的图象是（     ）  ‎ ‎20.如图，点C是以点O为圆心，AB为直径的半圆上的动点（点C不与点A，B重合），AB=4．设弦AC的长为x，△ABC的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是( )‎ 二 填空题:‎ ‎21.抛物线的部分图象如图所示，则当y＜0时，x的取值范围是_________．‎ ‎ ‎ ‎22.如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），该抛物线的对称轴为直线x=-1，若点C（﹣，y1），D（﹣，y2），E（，y3）均为函数图象上的点，则y1，y2，y3的大小关系为 ．‎ ‎23.二次函数y=ax2+bx+c的部分对应值如下表：‎ ‎ x ‎…‎ ‎﹣3‎ ‎﹣2 ‎ ‎0 ‎ ‎ 1‎ ‎3 ‎ ‎ 5‎ ‎…‎ ‎ y ‎…‎ ‎ 7‎ ‎ 0‎ ‎﹣8‎ ‎﹣9‎ ‎﹣5‎ ‎7 ‎ ‎…‎ ‎ 二次函数y=ax2+bx+c图象的对称轴为x=　　　　　，x=2对应的函数值y=　　　　　　．‎ ‎24.二次函数y=（x﹣1）2+1，当2≤y＜5时，相应x的取值范围为 ‎ ‎25.如图，在平面直角坐标系中，二次函数y=ax2+c（a≠0）的图象过正方形ABOC的三个顶点A、B、C，则ac的值是 ．‎ ‎ ‎ ‎ 第25题图 第26题图 ‎26.二次函数y=ax2+bx+c(a≠0)的图象如图所示，给出下列五条结论：‎ ‎ ①abc＜0；②4ac-b2＜0；③4a+c＜2b；④3b+2c＜0；⑤m(am+b)+b＜a（m≠-1）.‎ ‎ 其中正确的结论是         （把所有正确的结论的序号都填写在横线上） ‎ ‎27.小明从图示的二次函数y=ax2+bx+c的图象中，观察得出了下面4条信息：‎ ‎ ①abc＞0；②a﹣b+c＞0；③2a﹣3b=0；④c﹣4b＞0．你认为其中正确信息是　　　　　　（填序号）．‎ ‎ ‎ ‎　 第27题图 第28题图 ‎28.如图，平行于轴的直线分别交抛物线与于、两点，过点作轴的平行线交于点，直线∥，交于点，则       .‎ ‎29.如图，二次函数y=x(x-2)(0≤x≤2)的图象,记为C1，它与x轴交于O、A1两点；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，直至得C2016．若P（4031，m）在第2016段图象C2016上，则m=　　　　　　．‎ ‎ ‎ ‎　 第29题图 第30题图 三、解答题 ‎30.等腰三角形ABC以2米/秒的速度沿直线L向正方形移动，直到AB与CD重合。设x秒时，三角形与正方形重叠部分的面积为ym2。‎ ‎（1）写出y与x的关系式；‎ ‎（2）当x＝2，3.5时，y分别是多少？‎ ‎（3）当重叠部分的面积是正方形面积的一半时，三角形移动了多长时间？‎ ‎31.杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体(看成一点)的路线是抛物线的一部分,如图.‎ ‎（1）求演员弹跳离地面的最大高度；‎ ‎（2）已知人梯高BC＝3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由。‎ ‎32.二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：‎ ‎（1）一次函数和二次函数的解析式；‎ ‎（2）写出使一次函数值大于二次函数值的x的取值范围．‎ ‎33.如图，已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）求△MCB的面积S△MCB．‎ ‎34.某公司推出的高效环保洗条用品，年初上市后，经历了从亏损到盈利的过程，下面的二次函数的图象（部分）刻画了该公司年初以来累积利润S（万元）与销售时间t（月）之间的关系（即前t个月的利润总和S与t之间的关系）．‎ 根据图象提供的信息，解答系列问题：‎ ‎（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系 ‎（2）求第7个月公司所获利润为多少万元？‎ ‎35.如图，已知抛物线y=(x+2)(x﹣4)（k为常数,且k>0)与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y=﹣x+b与抛物线的另一交点为D．‎ ‎（1）若点D的横坐标为﹣5，求抛物线的函数表达式；‎ ‎（2）若在第一象限内的抛物线上有点P，使得以A，B，P为顶点的三角形与△ABC相似，求k的值；‎ ‎（3）在（1）的条件下，设F为线段BD上一点（不含端点），连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少？‎ 参考答案 ‎1、D 2、B 3、B 4、B 5、B 6、B 7、B 8、C 9、D 10、C 11、B 12、D 13、C ‎ ‎14、B 15、D 16、C  17、C 18、D 19、C 20、B  21、x＞3或x＜﹣1．22、y3＜y1＜y2　．  ‎ ‎23、﹣8　．24、﹣1＜x≤0或2≤x＜3　．25、﹣2　．26、 ②,④,⑤  27、①②④　（填序号）．‎ ‎28、 29、1　．‎ ‎30、解：（1）y=2x2（2）8；24.5（3）5秒 ‎31、解：（1）=‎ ‎∵，∴函数的最大值是。答：演员弹跳的最大高度是米。‎ ‎（2）当x＝4时，＝3.4＝BC，所以这次表演成功。‎ ‎32、【解答】解：（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），B（1，0），C（0，3），‎ 则，解得．故二次函数图象的解析式为y1=﹣x2﹣2x+3，‎ ‎∵对称轴x=﹣1，∴点D的坐标为（﹣2，3），设y2=kx+b，‎ ‎∵y2=kx+b过B、D两点，∴，解得．∴y2=﹣x+1；‎ ‎（2）函数的图象如图所示，‎ ‎∴当y2＞y1时，x的取值范围是x＜﹣2或x＞1．‎ ‎ ‎ ‎33、【解答】解：（1）依题意：，解得∴抛物线的解析式为y=﹣x2+4x+5‎ ‎（2）令y=0，得（x﹣5）（x+1）=0，x1=5，x2=﹣1，∴B（5，0）．‎ 由y=﹣x2+4x+5=﹣（x﹣2）2+9，得M（2，9）‎ 作ME⊥y轴于点E，可得S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC=（2+5）×9﹣×4×2﹣×5×5=15．‎ ‎34、【解答】解：（1）由图象可知其顶点坐标为（2，﹣2），故可设其函数关系式为：y=a（x﹣2）2﹣2．‎ ‎∵所求函数关系式的图象过（0，0），于是得：a（0﹣2）2﹣2=0，解得a=．‎ ‎∴所求函数关系式为：y=（x﹣2）2﹣2，即y=x2﹣2x．‎ 答：累积利润y与时间x之间的函数关系式为：y=x2﹣2x；‎ ‎（2）把x=6代入关系式，得y=×62﹣2×6=6，把x=7代入关系式，得y=×72﹣2×7=10.5，‎ ‎10.5﹣6=4.5，答：第7个月公司所获利是4.5万元．‎ ‎35、将AF+DF转化为AF+FG；再由垂线段最短，得到垂线段AH与直线BD的交点，即为所求的F点．‎ ‎【解答】解：（1）抛物线y=（x+2）（x﹣4），令y=0，解得x=﹣2或x=4，∴A（﹣2，0），B（4，0）．‎ ‎∵直线y=﹣x+b经过点B（4，0），∴﹣×4+b=0，解得b=，∴直线BD解析式为：y=﹣x+．‎ 当x=﹣5时，y=3，∴D（﹣5，3）．‎ ‎∵点D（﹣5，3）在抛物线y=（x+2）（x﹣4）上，‎ ‎∴（﹣5+2）（﹣5﹣4）=3，∴k=．∴抛物线的函数表达式为：y=（x+2）（x﹣4）．‎ ‎（2）方法一：由抛物线解析式，令x=0，得y=﹣k，∴C（0，﹣k），OC=k．‎ 因为点P在第一象限内的抛物线上，所以∠ABP为钝角．‎ 因此若两个三角形相似，只可能是△ABC∽△APB或△ABC∽△PAB．‎ ‎①若△ABC∽△APB，则有∠BAC=∠PAB，如答图2﹣1所示．‎ 设P（x，y），过点P作PN⊥x轴于点N，则ON=x，PN=y．‎ tan∠BAC=tan∠PAB，即：，∴y=x+k．‎ ‎∴P（x，x+k），代入抛物线解析式y=（x+2）（x﹣4），‎ 得（x+2）（x﹣4）=x+k，整理得：x2﹣6x﹣16=0，‎ 解得：x=8或x=﹣2（与点A重合，舍去），∴P（8，5k）．‎ ‎∵△ABC∽△APB，∴，即，解得：k=．‎ ‎②若△ABC∽△PAB，则有∠ABC=∠PAB，如答图2﹣2所示．‎ 与①同理，可求得：k=．综上所述，k=或k=．‎ 方法二：∵点P在第一象限内的抛物线上，∴∠ABP为钝角，‎ ‎①若△ABC∽△APB，则有∠BAC=∠PAB，∴KAP+KAC=0，‎ ‎∵C（0，﹣k），A（﹣2，0），∴KAC=﹣，∴KAP=，∵A（﹣2，0），∴lAP：y=x+k，‎ ‎∵抛物线：y=（x+2）（x﹣4），∴x2﹣6x﹣16=0，解得：x=8或x=2（舍）‎ ‎∴P（8，5k），∵△ABC∽△APB，∴，∴，∴k=，‎ ‎②若△ABC∽△APB，则有∠ABC=∠PAB，同理可得：k=；‎ ‎（3）方法一：如答图3，由（1）知：D（﹣5，3），如答图2﹣2，过点D作DN⊥x轴于点N，则DN=3，ON=5，BN=4+5=9，∴tan∠DBA===，∴∠DBA=30°．‎ 过点D作DK∥x轴，则∠KDF=∠DBA=30°．过点F作FG⊥DK于点G，则FG=DF．‎ 由题意，动点M运动的路径为折线AF+DF，运动时间：t=AF+DF，‎ ‎∴t=AF+FG，即运动的时间值等于折线AF+FG的长度值．‎ 由垂线段最短可知，折线AF+FG的长度的最小值为DK与x轴之间的垂线段．‎ 过点A作AH⊥DK于点H，则t最小=AH，AH与直线BD的交点，即为所求之F点．‎ ‎∵A点横坐标为﹣2，直线BD解析式为：y=﹣x+，‎ ‎∴y=﹣×（﹣2）+=2，∴F（﹣2，2）．‎ 综上所述，当点F坐标为（﹣2，2）时，点M在整个运动过程中用时最少．‎ 方法二：作DK∥AB，AH⊥DK，AH交直线BD于点F，‎ ‎∵∠DBA=30°，∴∠BDH=30°，∴FH=DF×sin30°=，∴当且仅当AH⊥DK时，AF+FH最小，‎ 点M在整个运动中用时为：t=，∵lBD：y=﹣x+，∴FX=AX=﹣2，∴F（﹣2，）．‎