九年级数学上册第一章特殊平行四边形3正方形的性质与判定第2课时正方形的判定教案新版北师大版 4页

第2课时　正方形的判定 ‎1．掌握正方形的判定定理，会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的证明和计算．‎ ‎2．经历探究正方形的判定定理的过程，发展学生综合推理的能力、主动探究的学习习惯，逐步掌握说理的基本方法．‎ ‎3．理解特殊的平行四边形之间的内在联系，培养学生辩证看问题的观点．‎ 重点 掌握正方形的判定定理．‎ 难点 合理恰当地利用特殊平行四边形的性质与判定进行有关的证明和计算．‎ 一、复习导入 ‎1．我们学习了平行四边形、矩形、菱形、正方形，那么思考一下，它们之间有怎样的包含关系？‎ ‎2．让学生回答以下问题：‎ ‎(1)怎样判断一个四边形是矩形？‎ ‎(2)怎样判断一个四边形是菱形？‎ ‎(3)怎样判断一个四边形是平行四边形？‎ ‎(4)怎样判断一个平行四边形是矩形、菱形？‎ 教师：你有什么方法判定一个四边形是正方形？这就是本节课要探究的内容．‎ 二、探究新知 ‎1．正方形的判定定理 课件出示教材第22页图1－20，提出问题：‎ 将一张长方形纸对折两次，然后剪下一个角，打开．怎样剪才能剪出一个正方形？‎ 学生动手操作，教师巡视指导，并讲解：‎ 因为正方形的两条对角线把它分成四个全等的等腰直角三角形，把折痕作对角线，这时只需剪一个等腰直角三角形，打开即是正方形，因此只要保证剪口线与折痕成45°角即可．‎ 教师：满足什么条件的矩形是正方形？满足什么条件的菱形是正方形？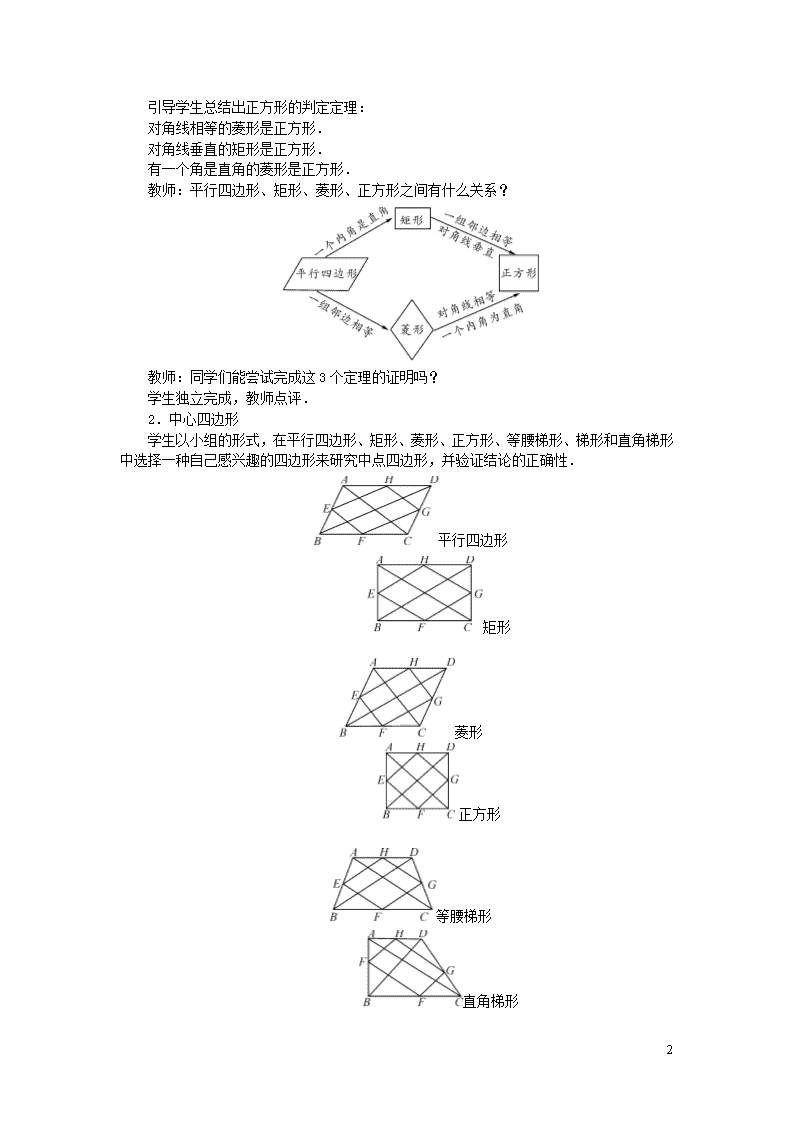‎ 4‎ 引导学生总结出正方形的判定定理：‎ 对角线相等的菱形是正方形．‎ 对角线垂直的矩形是正方形．‎ 有一个角是直角的菱形是正方形．‎ 教师：平行四边形、矩形、菱形、正方形之间有什么关系？‎ 教师：同学们能尝试完成这3个定理的证明吗？‎ 学生独立完成，教师点评．‎ ‎2．中心四边形 学生以小组的形式，在平行四边形、矩形、菱形、正方形、等腰梯形、梯形和直角梯形中选择一种自己感兴趣的四边形来研究中点四边形，并验证结论的正确性．‎ 平行四边形 ‎　　　　矩形 菱形 ‎　　　　正方形 等腰梯形 ‎　　　　直角梯形 4‎ 梯形 引导学生得出结论：‎ 平行四边形的中点四边形是平行四边形；‎ 矩形的中点四边形是菱形；‎ 菱形的中点四边形是矩形；‎ 正方形的中点四边形是正方形；‎ 等腰梯形的中点四边形是菱形；‎ 直角梯形的中点四边形是平行四边形；‎ 梯形的中点四边形是平行四边形．‎ 三、举例分析 例　如图，在矩形ABCD中，BE平分∠ABC，CE平分∠DCB，BF∥CE，CF∥BE.求证：四边形BECF是正方形．‎ 证明：∵BF∥CE，CF∥BE，‎ ‎∴四边形BECF是平行四边形．‎ ‎∵四边形ABCD是矩形，‎ ‎ ∴∠ABC＝90°，∠DCB＝90°.‎ 又∵BE平分∠ABC，CE平分∠DCB，‎ ‎∴∠EBC＝∠ABC＝45°，∠ECB＝∠DCB＝45°.‎ ‎∴∠EBC＝∠ECB.‎ ‎∴EB＝EC.‎ ‎∴▱BECF是菱形(菱形的定义)．‎ 在△EBC中，‎ ‎∵∠EBC＝45°，∠ECB＝45°，‎ ‎∴∠BEC＝90°.‎ ‎∴菱形BECF是正方形(有一个角是直角的菱形是正方形)．‎ 四、练习巩固 ‎1．教材第24页“随堂练习”．‎ ‎2．完成下列问题：‎ 图①‎ 4‎ ‎　图②‎ ‎　图③‎ ‎(1)如图①，在△ABC中，EF为△ABC的中位线．‎ ‎①若∠BEF＝30°，则∠A＝________. ‎ ‎②若EF＝8 cm，则AC＝________．‎ ‎(2)如图②，在AC的下方取一点D，连接AD，CD.取CD和AD的中点G、H，问EF和GH有怎样的关系？EH和FG呢？‎ ‎(3)如图③，四边形EFGH的形状有什么特征？‎ 五、小结 ‎1．通过本节课的学习，你有哪些收获？‎ ‎2．正方形的判定定理有哪些？‎ 六、课外作业 教材第25页习题1.8第1～4题．‎ 本节课采用了多媒体辅助教学，为学生创建了一个学习情境，通过图形的变换，使学生很容易发现问题的规律、找出解决方法，并且学生在老师的启发下，一步一步地探索、归纳、学习，在探索的过程中培养了学生的创新精神和意识．在小组讨论之前，应该留给学生充分的独立思考的时间，不要让一些思维活跃的学生的回答代替了其他学生的思考，掩盖了其他学生的疑问．‎ 4‎