2021年九年级数学中考一轮复习专题突破训练（填空题专项）：轴对称之线段最短问题（一） 19页

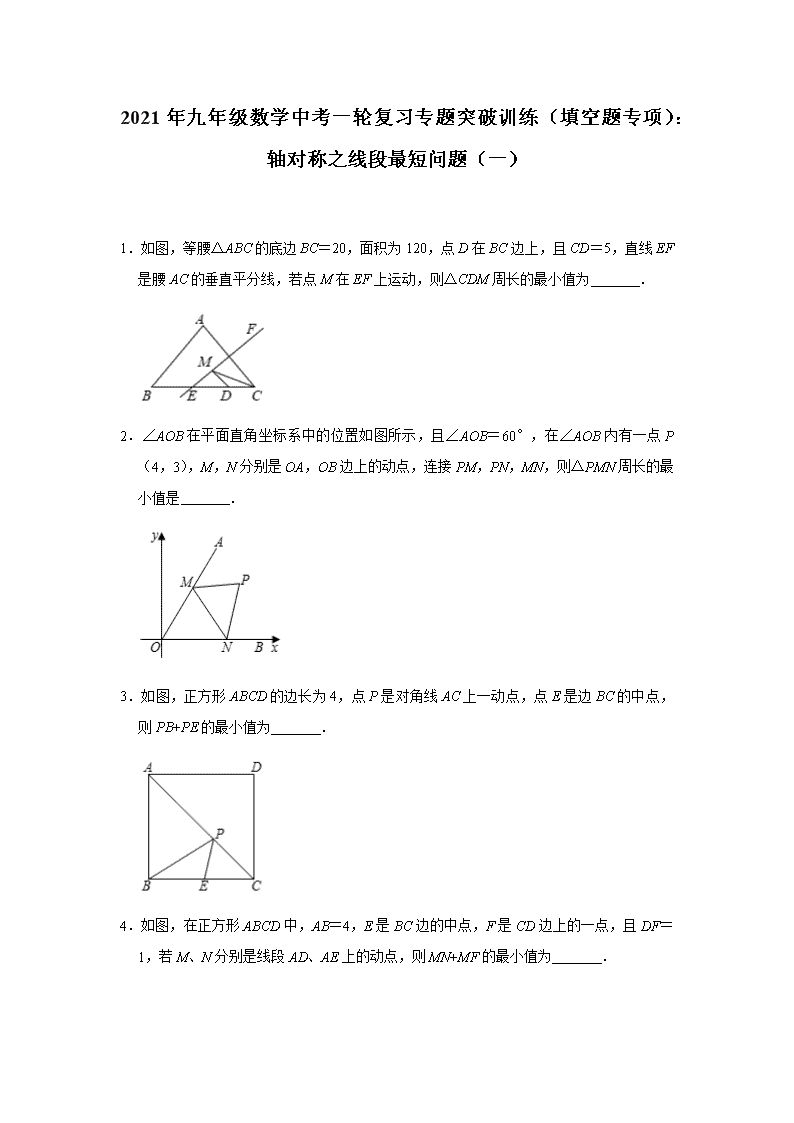
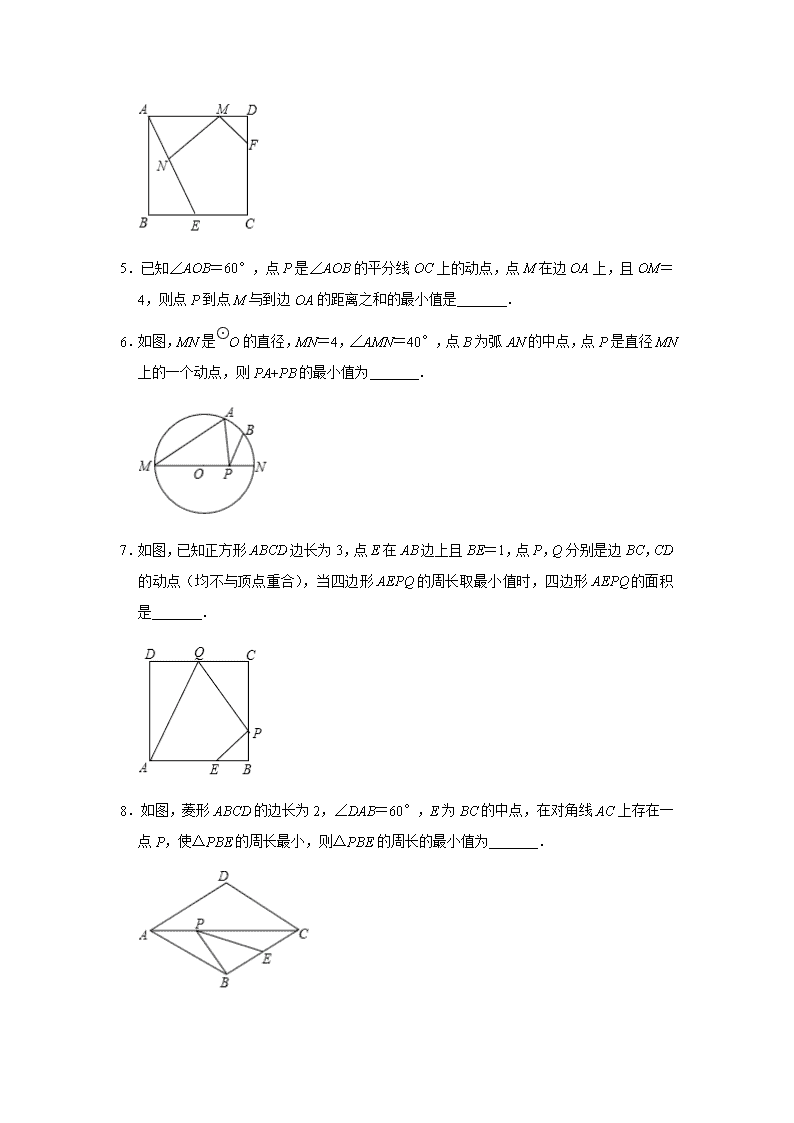
2021 年九年级数学中考一轮复习专题突破训练（填空题专项）： 轴对称之线段最短问题（一） 1．如图，等腰△ABC 的底边 BC＝20，面积为 120，点 D 在 BC 边上，且 CD＝5，直线 EF 是腰 AC 的垂直平分线，若点 M 在 EF 上运动，则△CDM 周长的最小值为 ． 2．∠AOB 在平面直角坐标系中的位置如图所示，且∠AOB＝60°，在∠AOB 内有一点 P（4， 3），M，N 分别是 OA，OB 边上的动点，连接 PM，PN，MN，则△PMN 周长的最小值 是 ． 3．如图，正方形 ABCD 的边长为 4，点 P 是对角线 AC 上一动点，点 E 是边 BC 的中点， 则 PB+PE 的最小值为 ． 4．如图，在正方形 ABCD 中，AB＝4，E 是 BC 边的中点，F 是 CD 边上的一点，且 DF＝1， 若 M、N 分别是线段 AD、AE 上的动点，则 MN+MF 的最小值为 ． 5．已知∠AOB＝60°，点 P 是∠AOB 的平分线 OC 上的动点，点 M 在边 OA 上，且 OM＝ 4，则点 P 到点 M 与到边 OA 的距离之和的最小值是 ． 6．如图，MN 是 ⊙ O 的直径，MN＝4，∠AMN＝40°，点 B 为弧 AN 的中点，点 P 是直径 MN 上的一个动点，则 PA+PB 的最小值为 ． 7．如图，已知正方形 ABCD 边长为 3，点 E 在 AB 边上且 BE＝1，点 P，Q 分别是边 BC， CD 的动点（均不与顶点重合），当四边形 AEPQ 的周长取最小值时，四边形 AEPQ 的面 积是 ． 8．如图，菱形 ABCD 的边长为 2，∠DAB＝60°，E 为 BC 的中点，在对角线 AC 上存在一 点 P，使△PBE 的周长最小，则△PBE 的周长的最小值为 ． 9．如图，∠AOB＝30°，点 M、N 分别是射线 OA、OB 上的动点，OP 平分∠AOB，且 OP ＝6，当△PMN 的周长取最小值时，四边形 PMON 的面积为 ． 10．如图，正方形 ABCD 的边长为 4，E 为 BC 上一点，BE＝1，F 为 AB 上一点，AF＝2， P 为 AC 上一点，则 PF+PE 的最小值为 ． 11．在每个小正方形的边长为 1 的网格中．点 A，B，C，D 均在格点上，点 E、F 分别为线 段 BC、DB 上的动点，且 BE＝DF． （Ⅰ）如图 ① ，当 BE＝ 时，计算 AE+AF 的值等于 （Ⅱ）当 AE+AF 取得最小值时，请在如图 ② 所示的网格中，用无刻度的直尺，画出线段 AE，AF，并简要说明点 E 和点 F 的位置如何找到的（不要求证明） ． 12．如图，在边长为 2 的等边△ABC 中，D 为 BC 的中点，E 是 AC 边上一点，则 BE+DE 的最小值为 ． 13．如图，正方形 ABCD 的边长为 2，点 E 为边 BC 的中点，点 P 在对角线 BD 上移动，则 PE+PC 的最小值是 ． 14．在 ⊙ O 中，AB 是 ⊙ O 的直径，AB＝8cm， ＝ ＝ ，M 是 AB 上一动点，CM+DM 的最小值是 cm． 15．如图，菱形 ABCD 中，对角线 AC＝6，BD＝8，M、N 分别是 BC、CD 的中点，P 是线 段 BD 上的一个动点，则 PM+PN 的最小值是 ． 16．如图，在边长为 4 的正方形 ABCD 中，E 是 AB 边上的一点，且 AE＝3，点 Q 为对角线 AC 上的动点，则△BEQ 周长的最小值为 ． 17．如图，菱形 ABCD 中，∠A＝60°，AB＝3， ⊙ A、 ⊙ B 的半径分别为 2 和 1，P、E、F 分别是边 CD、 ⊙ A 和 ⊙ B 上的动点，则 PE+PF 的最小值是 ． 18．在如图所示的平面直角坐标系中，点 P 是直线 y＝x 上的动点，A（1，0），B（2，0） 是 x 轴上的两点，则 PA+PB 的最小值为 ． 19．已知如图，直角梯形 ABCD 中，AD∥BC，AB⊥BC，AD＝2，BC＝DC＝5，点 P 在 BC 上移动，则当 PA+PD 取最小值时，△APD 中边 AP 上的高为 ． 20．如图，在等腰梯形 ABCD 中，AB＝AD＝2，∠BCD＝60°，对角线 AC 平分∠BCD，E， F 分别是底边 AD，BC 的中点，连接 EF．点 P 是 EF 上的任意一点，连接 PA，PB，则 PA+PB 的最小值为 ． 参考答案 1．解：如图，作 AH⊥BC 于 H，连接 AM， ∵EF 垂直平分线段 AC， ∴MA＝MC， ∴DM+MC＝AM+MD， ∴当 A、D、M 共线时，DM+MC 的值最小， ∵等腰△ABC 的底边 BC＝20，面积为 120，AH⊥BC， ∴BH＝CH＝10，AH＝ ＝12， ∴DH＝CH﹣CD＝5， ∴AD＝ ＝ ＝13， ∴DM+MC 的最小值为 13， ∴△CDM 周长的最小值＝13+5＝18， 故答案为 18． 2．解：分别作 P 关于射线 OA、射线 OB 的对称点 P′与点 P″，连接 P′P″，与 OA、OB 分别交于 M、N 两点， 此时△PMN 周长最小，最小值为 P′P″的长， 连接 OP′，OP″，OP， ∵OA、OB 分别为 PP′，PP″的垂直平分线，P（4，3）， ∴OP′＝OP＝OP″＝ ＝5，且∠POA＝∠P′OA，∠POB＝∠P″OB， ∵∠AOB＝∠AOP+∠BOP＝60°， ∴∠P′OP″＝120°， 过 O 作 OQ⊥P′P″，可得 P′Q＝P″Q，∠OP′Q＝∠OP″Q＝30°， ∴OQ＝ ，P′Q＝P″Q＝ ， ∴P′P″＝2P′Q＝2× ＝5 ， 则△PMN 周长的最小值是 5 ． 故答案为：5 ． 3．解：如图，连接 DE 交 AC 于点 P， 因为四边形 ABCD 是正方形， 所以点 B 和 D 关于 AC 对称， 所以 PB＝PD， 所以 PB+PE＝PD+PE＝DE， 根据两点之间线段最短， 可知：PB+PE 的最小值即为 DE 的长， 在 Rt△DEC 中，DC＝4，EC＝ BC＝2， 根据勾股定理，得 DE＝ ＝2 ． 所以 PB+PE 的最小值为 2 ． 故答案为：2 ． 4．解：作点 F 关于 AD 的对称点 G，过 G 作 GN⊥AE 与 N，交 AD 于 M， 则 GN 的长度等于 MN+MF 的最小值， ∵△DGM≌△DFM， ∴∠DMF＝∠GMD， ∵∠GMD＝∠AMN， ∵∠AMN+∠MAN＝∠MAN+∠BAE＝90°， ∴∠FMD＝∠BAE＝∠AMN， ∴△ABE∽△DMF∽△AMN， ∴ ， ∵AB＝4， ∴BE＝2， ∵DF＝1， ∴DM＝2， ∴AM＝2， ∵ ＝ ， ∴MN＝ ， ∵GM＝ ＝ ， ∴GN＝GM+MN＝MN+MF＝ ． ∴MN+MF 的最小值为 ， 故答案为： ． 5．解：过 M 作 MN′⊥OB 于 N′，交 OC 于 P， 则 MN′的长度等于 PM+PN 的最小值， 即 MN′的长度等于点 P 到点 M 与到边 OA 的距离之和的最小值， ∵∠ON′M＝90°，OM＝4， ∴MN′＝OM•sin60°＝2 ， ∴点 P 到点 M 与到边 OA 的距离之和的最小值为 2 ． 6．解：过 A 作关于直线 MN 的对称点 A′，连接 A′B，由轴对称的性质可知 A′B 即为 PA+PB 的最小值， 连接 OB，OA′，AA′， ∵AA′关于直线 MN 对称， ∴ ＝ ， ∵∠AMN＝40°， ∴∠A′ON＝80°，∠BON＝40°， ∴∠A′OB＝120°， 过 O 作 OQ⊥A′B 于 Q， 在 Rt△A′OQ 中，OA′＝2， ∴A′B＝2A′Q＝2 ， 即 PA+PB 的最小值 2 ． 故答案为：2 ． 7．解：如图 1 所示： 作 E 关于 BC 的对称点 E′，点 A 关于 DC 的对称点 A′，连接 A′E′，四边形 AEPQ 的周长最小， ∵AD＝A′D＝3，BE＝BE′＝1， ∴AA′＝6，AE′＝4． ∵DQ∥AE′，D 是 AA′的中点， ∴DQ 是△AA′E′的中位线， ∴DQ＝ AE′＝2；CQ＝DC﹣DQ＝3﹣2＝1， ∵BP∥AA′， ∴△BE′P∽△AE′A′， ∴ ＝ ，即 ＝ ，BP＝ ，CP＝BC﹣BP＝3﹣ ＝ ， S 四边形 AEPQ＝S 正方形 ABCD﹣S△ADQ﹣S△PCQ﹣SBEP ＝9﹣ AD•DQ﹣ CQ•CP﹣ BE•BP ＝9﹣ ×3×2﹣ ×1× ﹣ ×1× ＝ ． 故答案为： ． 8．解：连接 DE． ∵BE 的长度固定， ∴要使△PBE 的周长最小只需要 PB+PE 的长度最小即可， ∵四边形 ABCD 是菱形， ∴AC 与 BD 互相垂直平分， ∴P′D＝P′B， ∴PB+PE 的最小长度为 DE 的长， ∵菱形 ABCD 的边长为 2，E 为 BC 的中点，∠DAB＝60°， ∴△BCD 是等边三角形， 又∵菱形 ABCD 的边长为 2， ∴BD＝2，BE＝1，DE＝ ， ∴△PBE 的最小周长＝DE+BE＝ +1， 故答案为： +1． 9．解：分别作点 P 关于 OA、OB 的对称点 C、D，连接 CD，分别交 OA、OB 于点 M、N， 连接 OC、OD、PC、PD． ∵点 P 关于 OA 的对称点为 C，关于 OB 的对称点为 D， ∴PM＝CM，OP＝OC，∠COA＝∠POA； ∵点 P 关于 OB 的对称点为 D， ∴PN＝DN，OP＝OD，∠DOB＝∠POB， ∴OC＝OD＝OP＝6，∠COD＝∠COA+∠POA+∠POB+∠DOB＝2∠POA+2∠POB＝2∠ AOB＝60°， ∴△COD 是等边三角形， ∴CD＝OC＝OD＝6． ∵∠POC＝∠POD， ∴OP⊥CD， ∴OQ＝6× ＝3 ， ∴PQ＝6﹣3 设 MQ＝x，则 PM＝CM＝3﹣x， ∴（3﹣x）2﹣x2＝（6﹣3 ）2，解得 x＝6 ﹣9， ∴MN＝2MQ＝12 ﹣18， ∵S△PMN＝ MN×PQ， S△MON＝ MN×OQ， ∴S 四边形 PMON＝S△MON+S△PMN＝ MN×PQ+ MN×OQ＝ MN×OP＝ ×（12 ﹣18） ×6＝36 ﹣54． 故答案为 36 ﹣54． 10．解：作 E 关于直线 AC 的对称点 E′，连接 E′F，则 E′F 即为所求， 过 F 作 FG⊥CD 于 G， 在 Rt△E′FG 中， GE′＝CD﹣BE﹣BF＝4﹣1﹣2＝1，GF＝4， 所以 E′F＝ ． 故答案为： ． 11．解：（1）根据勾股定理可得：DB＝ ， 因为 BE＝DF＝ ， 所以可得 AF＝ ＝2.5， 根据勾股定理可得：AE＝ ，所以 AE+AF＝ ， 故答案为： ； （2）如图， 首先确定 E 点，要使 AE+AF 最小，根据三角形两边之和大于第三边可知，需要将 AF 移 到 AE 的延长线上，因此可以构造全等三角形，首先选择格点 H 使∠HBC＝∠ADB，其 次需要构造长度 BP 使 BP＝AD＝4，根据勾股定理可知 BH＝ ＝5，结合相似三 角形选出格点 K，根据 ，得 BP＝ BH＝ ＝4＝DA，易证△ADF≌△ PBE，因此可得到 PE＝AF，线段 AP 即为所求的 AE+AF 的最小值；同理可确定 F 点， 因为 AB⊥BC，因此首先确定格点 M 使 DM⊥DB，其次确定格点 G 使 DG＝AB＝3，此 时需要先确定格点 N，同样根据相似三角形性质得到 ，得 DG＝ DM＝ × 5＝3，易证△DFG≌△BEA，因此可得到 AE＝GF，故线段 AG 即为所求的 AE+AF 的最 小值． 故答案为：取格点 H，K，连接 BH，CK，相交于点 P，连接 AP，与 BC 相交，得点 E， 取格点 M，N 连接 DM，CN，相交于点 G，连接 AG，与 BD 相交，得点 F，线段 AE， AF 即为所求． 12．解：作 B 关于 AC 的对称点 B′，连接 BB′、B′D，交 AC 于 E，此时 BE+ED＝B′ E+ED＝B′D，根据两点之间线段最短可知 B′D 就是 BE+ED 的最小值， ∵B、B′关于 AC 的对称， ∴AC、BB′互相垂直平分， ∴四边形 ABCB′是平行四边形， ∵三角形 ABC 是边长为 2， ∵D 为 BC 的中点， ∴AD⊥BC， ∴AD＝ ，BD＝CD＝1，BB′＝2AD＝2 ， 作 B′G⊥BC 的延长线于 G， ∴B′G＝AD＝ ， 在 Rt△B′BG 中， BG＝ ＝ ＝3， ∴DG＝BG﹣BD＝3﹣1＝2， 在 Rt△B′DG 中，B′D＝ ＝ ＝ ． 故 BE+ED 的最小值为 ． 故答案为： ． 13．解：如图，连接 AE， ∵点 C 关于 BD 的对称点为点 A， ∴PE+PC＝PE+AP， 根据两点之间线段最短可得 AE 就是 AP+PE 的最小值， ∵正方形 ABCD 的边长为 2，E 是 BC 边的中点， ∴BE＝1， ∴AE＝ ＝ ， 故答案为： ． 14．解：如图，作点 C 关于 AB 的对称点 C′，连接 C′D 与 AB 相交于点 M， 此时，点 M 为 CM+DM 的最小值时的位置， 由垂径定理， ＝ ， ∴ ＝ ， ∵ ＝ ＝ ，AB 为直径， ∴C′D 为直径， ∴CM+DM 的最小值是 8cm． 故答案为：8． 15．解：作 M 关于 BD 的对称点 Q，连接 NQ，交 BD 于 P，连接 MP，此时 MP+NP 的值最 小，连接 AC， ∵四边形 ABCD 是菱形， ∴AC⊥BD，∠QBP＝∠MBP， 即 Q 在 AB 上， ∵MQ⊥BD， ∴AC∥MQ， ∵M 为 BC 中点， ∴Q 为 AB 中点， ∵N 为 CD 中点，四边形 ABCD 是菱形， ∴BQ∥CD，BQ＝CN， ∴四边形 BQNC 是平行四边形， ∴NQ＝BC， ∵AQ＝CN，∠QAP＝∠PCN，∠APQ＝∠CPN， ∴△APQ≌△CPN（AAS）， ∴AP＝PC， ∵四边形 ABCD 是菱形， ∴CP＝ AC＝3，BP＝ BD＝4， 在 Rt△BPC 中，由勾股定理得：BC＝5， 即 NQ＝5， ∴MP+NP＝QP+NP＝QN＝5， 故答案为：5． 16．解：连接 BD，DE， ∵四边形 ABCD 是正方形， ∴点 B 与点 D 关于直线 AC 对称， ∴DE 的长即为 BQ+QE 的最小值， ∵DE＝BQ+QE＝ ＝ ＝5， ∴△BEQ 周长的最小值＝DE+BE＝5+1＝6． 故答案为：6． 17．解：作 A 点关于直线 DC 的对称点 A′，连接 AA′，延长 CD 交 AA′于点 N，连接 BD， DA′， ∵四边形 ABCD 是菱形， ∴AB＝AD， ∵∠BAD＝60°， ∴△ADB 是等边三角形， ∴∠ADB＝60°， ∵∠BDC＝∠ADB＝60°， ∴∠ADN＝60°， ∴∠A′DN＝60°， ∴∠ADB+∠ADA′＝180°， ∴A′，D，B 在一条直线上， 由题意可得出：此时 P 与 D 重合，E 点在 AD 上，F 在 BD 上，此时 PE+PF 最小， ∵菱形 ABCD 中，∠A＝60°， ∴AB＝AD，则△ABD 是等边三角形， ∴BD＝AB＝AD＝3， ∵ ⊙ A、 ⊙ B 的半径分别为 2 和 1， ∴PE＝1，PF＝2， ∴PE+PF 的最小值是 3． 故答案为：3． 18．解：如图所示：作 A 点关于直线 y＝x 的对称点 A′，连接 A′B，交直线 y＝x 于点 P， 此时 PA+PB 最小， 由题意可得出：OA′＝1，BO＝2，PA′＝PA， ∴PA+PB＝A′B＝ ＝ ． 故答案为： ． 19．解：过点 D 作 DE⊥BC 于 E， ∵AD∥BC，AB⊥BC， ∴四边形 ABED 是矩形， ∴BE＝AD＝2， ∵BC＝CD＝5， ∴EC＝3， ∴AB＝DE＝4， 延长 AB 到 A′，使得 A′B＝AB，连接 A′D 交 BC 于 P，此时 PA+PD 最小， ∴△A′PB≌△DPE， ∴BP＝EP， ∴PA＝PD， ∴BP＝ AD＝1， ∴AP＝ ， 在△APD 中，由面积公式可得 △APD 中边 AP 上的高＝2×4÷ ＝ ． 故答案为： ． 20．解：∵E，F 分别是底边 AD，BC 的中点，四边形 ABCD 是等腰梯形， ∴B 点关于 EF 的对称点 C 点， ∴AC 即为 PA+PB 的最小值， ∵∠BCD＝60°，对角线 AC 平分∠BCD， ∴∠ABC＝60°，∠BCA＝30°， ∴∠BAC＝90°， ∵AD＝2， ∴PA+PB 的最小值＝AB•tan60°＝ ． 故答案为：2 ．