2020九年级数学下册 第2章正多边形与圆 5页

‎2.7　正多边形与圆 知|识|目|标 ‎1．通过对多边形的边角比较，归纳出正多边形的概念及相关性质．‎ ‎2．通过回顾尺规作图，掌握画圆的内接正多边形的方法．‎ ‎3．通过操作与讨论，理解正多边形的对称性，并能进行相关计算．‎ 目标一　理解正多边形的有关概念 例1 教材补充例题下列说法正确的是(　　)‎ A．各边相等的多边形是正多边形 B．各角相等的多边形是正多边形 C．各边相等的圆内接多边形是正多边形 D．各角相等的圆内接多边形是正多边形 ‎【归纳总结】正多边形及其有关概念：‎ ‎(1)正多边形的定义包含了正多边形的基本性质：①各边相等；②各角相等．‎ ‎(2)正多边形的判定方法：同时满足条件：①各边相等；②各角相等的多边形是正多边形．‎ 目标二　会画正多边形 例2 教材补充例题已知⊙O和⊙O上的一点A，如图2－7－1所示．‎ ‎(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH；‎ ‎(2)在(1)题所作的图中，如果点E在劣弧AB上，试证明EB是⊙O内接正十二边形的一边．‎ 5‎ 图2－7－1‎ ‎【归纳总结】等分圆周画正多边形的工具和方法：‎ ‎(1)只用量角器：用量角器把360°圆心角n等分，相应圆周也n等分，顺次连接各分点得到正n边形．‎ ‎(2)用量角器和圆规：先用量角器画出360°圆心角的n分之一，从而得到圆周的n分之一，再用圆规顺次截取，便得圆周的n等分点，顺次连接各分点得到正n边形．‎ ‎(3)用圆规和直尺：用尺规等分圆周，可以作正六边形、正方形等特殊正多边形．‎ 目标三　能进行正多边形的有关计算 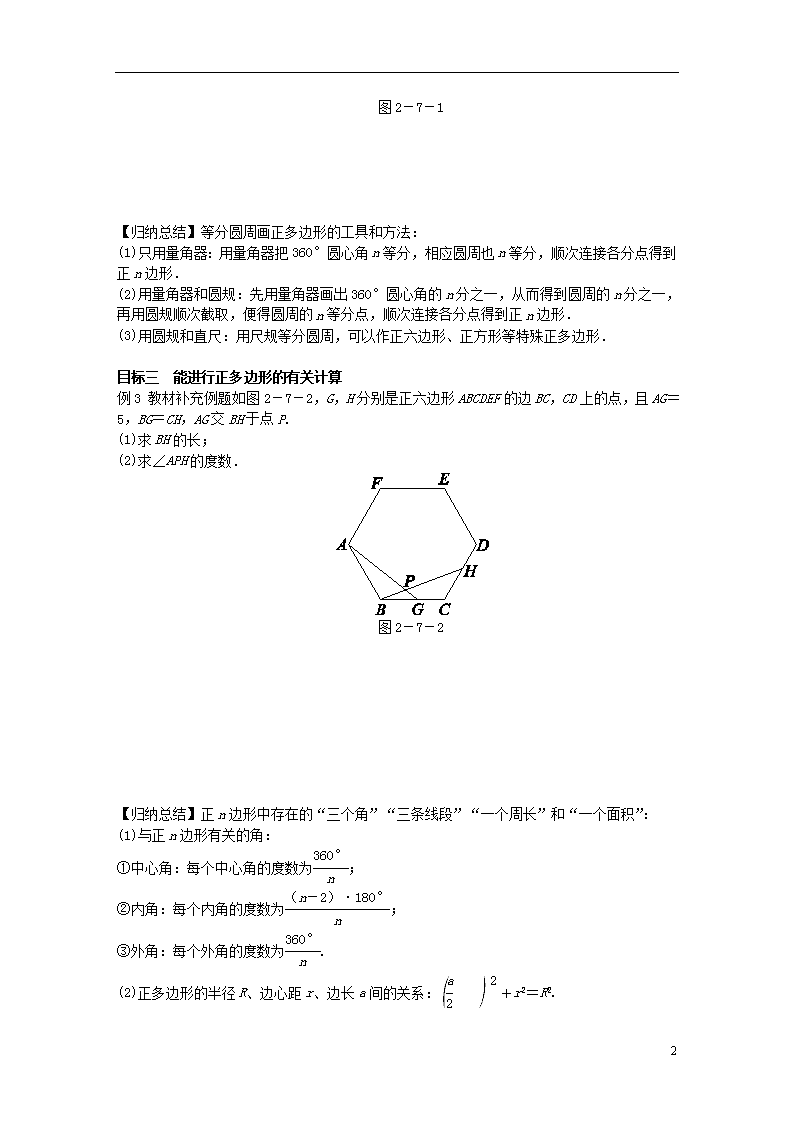例3 教材补充例题如图2－7－2，G，H分别是正六边形ABCDEF的边BC，CD上的点，且AG＝5，BG＝CH，AG交BH于点P.‎ ‎(1)求BH的长；‎ ‎(2)求∠APH的度数．‎ 图2－7－2‎ ‎【归纳总结】正n边形中存在的“三个角”“三条线段”“一个周长”和“一个面积”：‎ ‎(1)与正n边形有关的角：‎ ‎①中心角：每个中心角的度数为；‎ ‎②内角：每个内角的度数为；‎ ‎③外角：每个外角的度数为.‎ ‎(2)正多边形的半径R、边心距r、边长a间的关系：＋r2＝R2.‎ 5‎ ‎(3)正n边形的周长l与边长a，面积S与边长a、边心距r间的关系：周长l＝na；面积S＝arn.‎ 知识点一　正多边形的有关概念 正多边形：各边相等，各内角也相等的多边形叫作正多边形．‎ 将一个圆n(n≥3)等分，依次连接各等分点所得的多边形叫作这个圆的内接正多边形，这个圆是这个正多边形的外接圆，正多边形的外接圆的圆心叫作正多边形的中心．‎ 5‎ 知识点二　正多边形的画法 基本原理：由于在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，因此可以用等分圆心角的方法来等分圆周， 画正多边形．‎ 常用方法：(1)用量角器等分；‎ ‎(2)用圆规等分．‎ 知识点三　正多边形的对称性 正多边形都是轴对称图形，一个正n边形共有____条对称轴，每条对称轴都通过正n边形的______．当n为奇数时，正n边形的n条对称轴都是顶点与中心的连线所在的直线；当n为偶数时，正n边形有____条对称轴是过顶点与中心的直线，有____条对称轴是过中心与边垂直的直线．‎ 正偶数边形都是中心对称图形，它的对称中心是这个正多边形的中心．‎ 判断：正多边形都是中心对称图形．(　　)‎ 答案：√‎ 以上答案正确吗？若不正确，请说明理由．‎ 5‎ 教师详解详析 ‎【目标突破】‎ 例1　[解析] C　通过举反例可以知道菱形的各边相等，但它不是正多边形，可以排除选项A，矩形各角相等，但它不是正多边形，可以排除选项B，D.‎ 例2　[解析] (1)根据正方形和正六边形的作图方法分别作出⊙O的内接正方形ABCD和内接正六边形AEFCGH；‎ ‎(2)通过计算EB所对的圆心角的度数来证明．‎ 解：(1)在⊙O中，用直尺和圆规作两条互相垂直的直径AC和BD，连接AB，BC，CD，DA，得⊙O的内接正方形ABCD(如图所示)；按正六边形的作法用直尺和圆规在⊙O中作出正六边形AEFCGH.‎ ‎(2)证明：连接OE.‎ ‎∵AE是正六边形的一边，‎ ‎∴∠AOE＝＝60°.‎ ‎∵AB是正方形的一边，‎ ‎∴∠AOB＝＝90°，‎ ‎∴∠BOE＝∠AOB－∠AOE＝90°－60°＝30°.‎ 设EB是⊙O内接正n边形的一边，‎ 则＝30°，解得n＝12，‎ ‎∴EB是⊙O内接正十二边形的一边．‎ 例3　解：(1)在正六边形ABCDEF中，AB＝BC，∠ABC＝∠C＝120°.在△ABG与△BCH中，‎ ‎∵ ‎∴△ABG≌△BCH，∴BH＝AG＝5.‎ ‎(2)由(1)知△ABG≌△BCH，∴∠BAG＝∠CBH，∴∠BPG＝∠ABG＝120°，∴∠APH＝∠BPG＝120°.‎ ‎【总结反思】‎ ‎[小结] 知识点三　n　中心　　 ‎[反思] 不正确．因为只有正偶数边形才是中心对称图形．‎ 反思：正偶数边形既是中心对称图形，又是轴对称图形；正奇数边形仅是轴对称图形．‎ 5‎