13年1月黄浦中考数学一模试题 7页

黄浦区 2012 学年第一学期九年级期终考试数学试卷 （满分 150 分，考试时间 100 分钟） 2013 年 1 月 17 日 考生注意： 1、本试卷含四个大题，共 25 题； 2、答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律 无效； 3、除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计 算的主要步骤。 一、选择题（本大题共 6 题，每题 4 分，满分 24 分） 1、如果△ABC∽△DEF（其中顶点 A、B、C 依次与顶点 D、E、F 对应），那么下列等式中 不一定成立的是（ ） A、∠A＝∠D B、 AD BE  C、AB＝DE D、 AB DE AC DF 2、如图，地图上 A 地位于 B 地的正北方，C 地位于 B 地的北偏东 50°方向，且 C 地到 A 地、 B 地距离相等，那么 C 地位于 A 地的（ ） A、南偏东 50°方向 B、北偏西 50°方向 C、南偏东 40°方向 D、北偏西 40°方向 3、将抛物线 2yx 向左平移 2 个单位，则所得的抛物线的解析式为（ ） A、 2( 2)yx B、 2( 2)yx C、 2 2yx D、 2 2yx 4、如图，△PQR 在边长为 1 个单位的方格纸中，它的顶点在小正方形顶点位置，其中点 A、 B、C、D 也是小正方形的顶点，那么与△PQR 相似的是（ ） A、以点 P、Q、A 为顶点的三角形 B、以点 P、Q、B 为顶点的三角形 C、以点 P、Q、C 为顶点的三角形 D、以点 P、Q、D 为顶点的三角形 C B A （第 2 题） Q R P D C B A （第 4 题） A B D C （第 6 题） 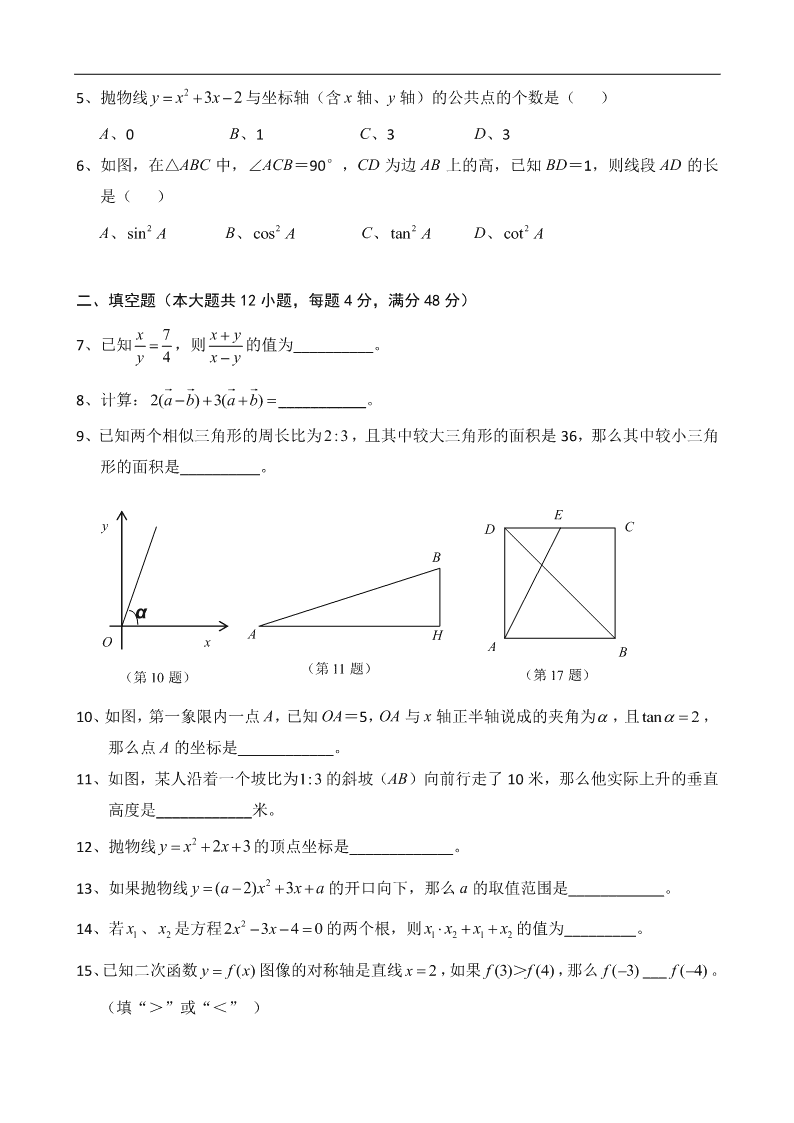5、抛物线 2 32y x x   与坐标轴（含 x 轴、y 轴）的公共点的个数是（ ） A、0 B、1 C、3 D、3 6、如图，在△ABC 中，∠ACB＝90°，CD 为边 AB 上的高，已知 BD＝1，则线段 AD 的长 是（ ） A、 2sin A B、 2cos A C、 2tan A D、 2cot A 二、填空题（本大题共 12 小题，每题 4 分，满分 48 分） 7、已知 7 4 x y  ，则 xy xy   的值为__________。 8、计算： 2( ) 3( )a b a b   ___________。 9、已知两个相似三角形的周长比为 2:3，且其中较大三角形的面积是 36，那么其中较小三角 形的面积是__________。 10、如图，第一象限内一点 A，已知 OA＝5，OA 与 x 轴正半轴说成的夹角为 ，且 tan 2  ， 那么点 A 的坐标是____________。 11、如图，某人沿着一个坡比为1:3的斜坡（AB）向前行走了 10 米，那么他实际上升的垂直 高度是____________米。 12、抛物线 2 23y x x   的顶点坐标是_____________。 13、如果抛物线 2( 2) 3y a x x a    的开口向下，那么 a 的取值范围是____________。 14、若 1x 、 2x 是方程 22 3 4 0xx   的两个根，则 1 2 1 2x x x x   的值为_________。 15、已知二次函数 ()y f x 图像的对称轴是直线 2x  ，如果 (3) (4)ff＞ ，那么 ( 3)f  ___ ( 4)f  。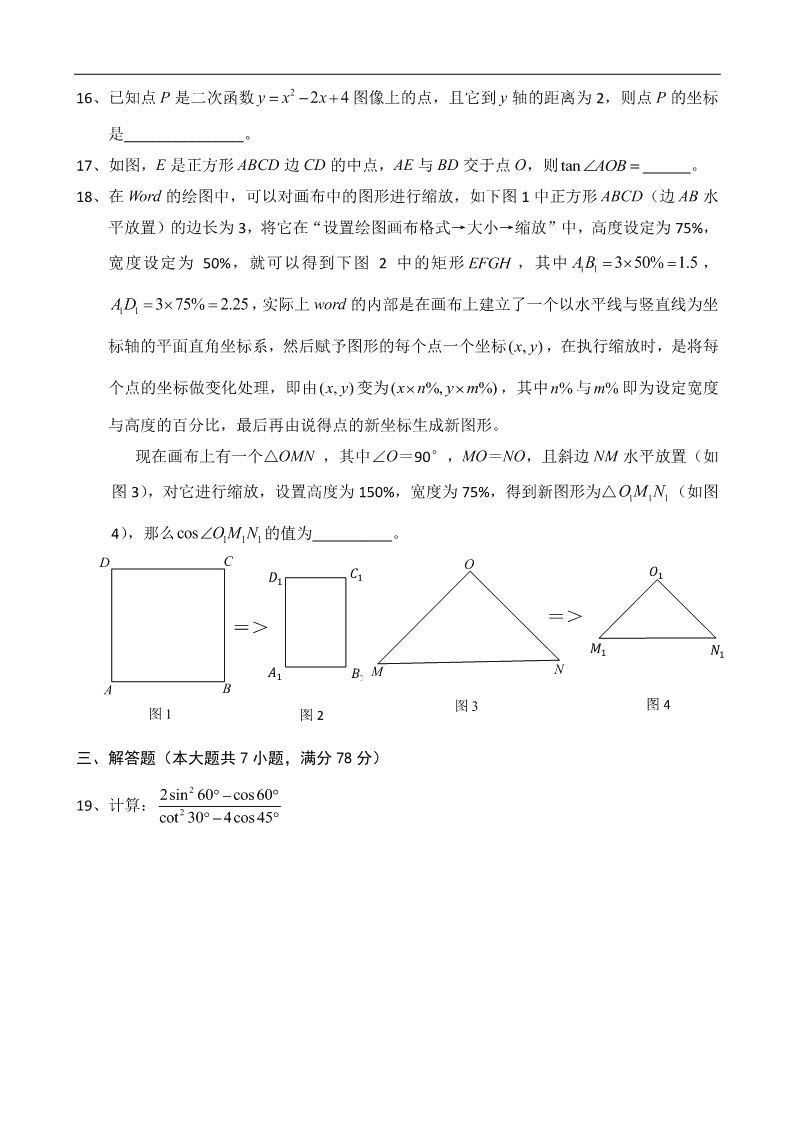 （填“＞”或“＜” ） α y x O （第 10 题） H B A （第 11 题） （第 17 题） A B C D E 16、已知点 P 是二次函数 2 24y x x   图像上的点，且它到 y 轴的距离为 2，则点 P 的坐标 是_______________。 17、如图，E 是正方形 ABCD 边 CD 的中点，AE 与 BD 交于点 O，则 tan AOB______。 18、在 Word 的绘图中，可以对画布中的图形进行缩放，如下图 1 中正方形 ABCD（边 AB 水 平放置）的边长为 3，将它在“设置绘图画布格式→大小→缩放”中，高度设定为 75%， 宽度设定为 50%，就可以得到下图 2 中的矩形 EFGH ，其中 11 3 50% 1.5AB    ， 11 3 75% 2.25AD    ，实际上 word 的内部是在画布上建立了一个以水平线与竖直线为坐 标轴的平面直角坐标系，然后赋予图形的每个点一个坐标( , )xy，在执行缩放时，是将每 个点的坐标做变化处理，即由( , )xy变为( %, %)x n y m，其中 %n 与 %m 即为设定宽度 与高度的百分比，最后再由说得点的新坐标生成新图形。 现在画布上有一个△OMN ，其中∠O＝90°，MO＝NO，且斜边 NM 水平放置（如 图 3），对它进行缩放，设置高度为 150%，宽度为 75%，得到新图形为△ 1 1 1O M N （如图 4），那么 1 1 1cos O M N 的值为__________。 三、解答题（本大题共 7 小题，满分 78 分） 19、计算： 2 2 2sin 60 cos60 cot 30 4cos 45       ＝＞ B A D C 图 1 图 2 ＝＞ N M O 图 3 图 4 20、如图，点 E 是平行四边形 ABCD 边 BC 上一点，且 : 2:1BE EC  ，点 F 是边 CD 的中点， AE 与 BF 交于点 O， （1）设 ,AB a AD b，试用 a 、b 表示 AE ； （2）求 :BO OF 的值。 21、已知二次函数的图像经过点(0, 8) 和(3, 5) ，且其对称轴是直线 1x  ，求此二次函数的 解析式，并求出次二次函数图像与 x 轴公共点的坐标。 22、如图，在△ABC 中， 90C  ，AC＝4，BC＝6，点 D 是边 BC 上一点，且 CAD B   。 （1）求线段 CD 的长； （2）求sin BAD 的值。 O F E D C B A D B C A 23、如图，点 D 是 Rt△ABC 斜边 AB 上一点，点 E 是直线 AC 左侧一点，且 EC⊥CD，∠EAB ＝∠B。 （1）求证：△CDE∽△CBA； （2）如果点 D 是斜边 AB 中点，且 3tan 2BAC，试求 CDE CBA S S 的值。 （ CDES 表示△CDE 的面积， CBAS 表示△CBA 的面积） 24、已知二次函数 2 3y ax bx   的图像与 x 轴交于点 (1,0)A 和点 (3,0)B ，交 y 轴于点 C，其 图像顶点为 D。 （1）求此二次函数的解析式； （2）是问△ABD 与△BCO 是否相似，并证明你的结论； （3）若点 P 是此二次函数图像上的点，且 PAB ACB   ，试求点 P 的坐标。 O y x A B C D E 25、如图，在等腰三角形 ABCD 中，AD∥BC，AD＝2，AB＝5， 3sin 5B，点 E 是边 BC 上的一个动点（不与点 B、C 重合）作 AEF AEB   ，使边 EF 交边 CD 于点 F（不与 点 C、D 重合），设 ,BE x CF y。 （1）求边 BC 的长； （2）当△ABE 与△CEF 相似时，求 BE 的长； （3）求 y 关于 x 的函数关系式，并写出定义域。 F E C B D A C B D A （备用图） 黄浦区一模参考答案 一、选择题 CAABDD 二、填空题 7、11 3 8、5ab 9、16 10、( 5,2 5) 11、 10 12、( 1,2) 13、a＜2 14、 1 2 15、＞ 16、(2,4) ，( 2,12) 17、3 18、 5 5 三、解答题 19、3 2 2 20、（ 1） 2 3AE a b ；（ 2） :BO OF 的值为 1 21、 2 28y x x   ，公共点为( 2,0) 与(4,0) 22、（ 1） 8 3CD  ；（ 2） 5sin 13BAD 23、（2） 13 36 CDE CBA S S  24、（ 1） 2 43y x x   ；（ 2）是相似，利用三边对应成比例来证明；（3） 53( , )24 或 75( , )24 25、（ 1） 10BC  ；（ 2） 43BE  或 10；（ 3） 2 2 10 140 400 16 39 xxy xx   （4＜x＜10）