2020年江苏省泰州市中考数学真题 8页

泰州市二 ◯ 二 ◯ 年初中学业水平测试 数学试题 （考试时间：120 分钟 满分 150 分） 请注意：1. 本试卷分选择题和非选择题两个部分. 2.所有试题的答案均填写在答题卡上，答案写在试卷上无效. 3.作图必须用 2B 铅笔，并请加黑加粗. 第一部分 选择题（区 18 分） 一、选择题：（本大题共有 6 小题，第小题 3 分，共 18 分.在每小题所给出的四个选项中，恰有一项是符 合题目要求的，请将正确选项的字母代号填涂在 答 ∙ 题∙ 卡 ∙ 相∙ 应∙ 位 ∙ 置∙ 上） 1. -2 的倒数是 A. 2 B. 1 2  C. -2 D. - 1 2  2. 把如图所示的纸片沿着虚线折叠，可以得到的几何体是 A. 三棱柱 B. 四棱柱 C. 三棱锥 D. 四棱锥 3. 下列等式成立的是 A. 3 + 4 2  = 7 2  B. 3  × 2  = 5  C. 3  ÷ 1 6  = 2 3  D. (-3)2  = 3 4. 如图，电路图上有 4 个开关 A、B、C、D 和 1 个小灯泡，同时闭合开关 A、B 或同时闭合开关 C、D 都可以使小灯泡发光.下列操作中，“小灯泡发光”这 个事件是随机事件的是 A. 只闭合 1 个开关 B. 只闭合 2 个开关 C. 只闭合 3 个开关 D. 闭合 4 个开关 5. 点 P(a, b) 在函数 y = 3x + 2 的图像上，则代数式 6a - 2b + 1 的值等于 A. 5 B. 3 C. -3 D. -1 6. 如图，半径为 10 的扇形 AOB 中，∠ AOB = 90°，C 为 AB  上一点，CD ⊥ OA, CE ⊥ OB, 垂足分别为 D、E. 若 ∠ CDE 为 36°, 则图中阴影部分的面积为 A. 10π B. 9π C. 8π D. 6π （第2题图） A B C D （第4题图） A B CD EO （第6题图） 第二部分 非选择题（共 132 分） 二、填空题（本大题共有 10 小题，每小题 3 分，共 30 分，请把答案直接填写在 答 ∙ 题∙ 卡 ∙ 相∙ 应∙ 位 ∙ 置∙ 上） 7. 9 的平方根等于 _____. 8. 因式分解：x2 - 4 = ____. 9. 据新华社 2020 年 5 月 17 日消息，全国各地和军队约 42600 名医务人员支援湖北抗击新冠肺炎疫 情，将 42600 用科学计数法表示为 _______. 10. 方程 x2 + 2x - 3 = 0 的两根为 x1、x2,则 x1 ∙ x2 的值为 ________. 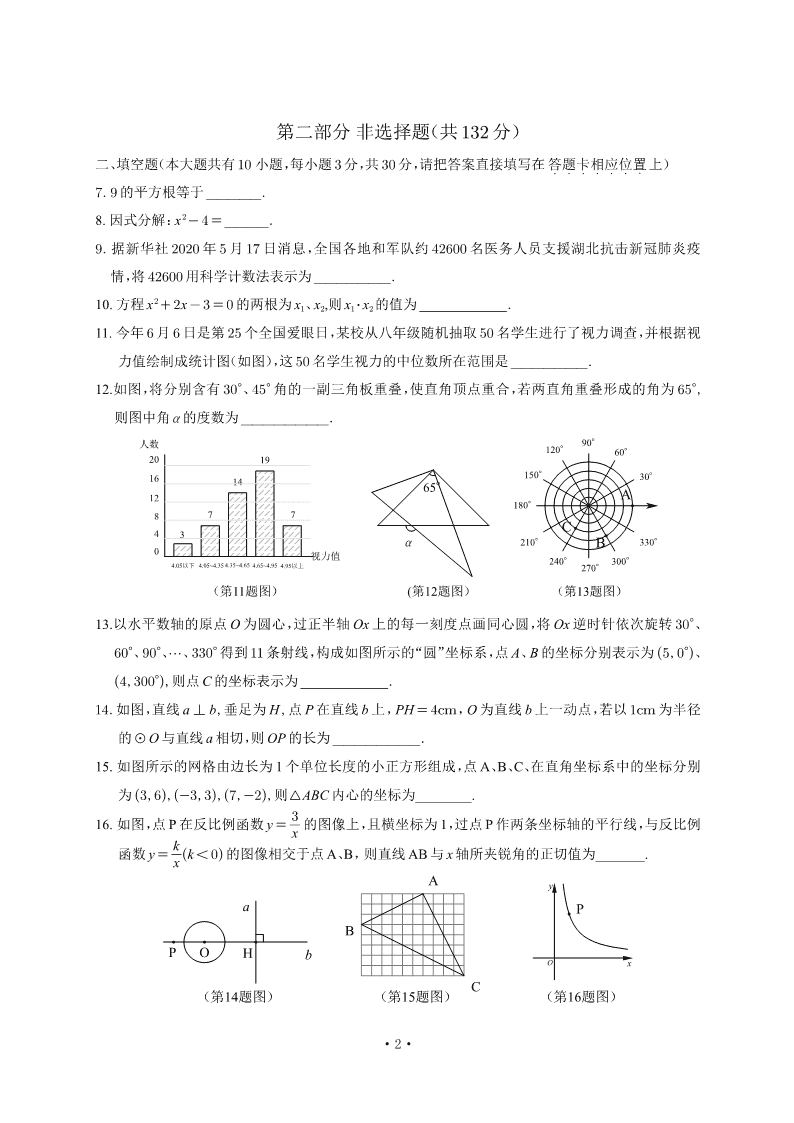11. 今年 6 月 6 日是第 25 个全国爱眼日，某校从八年级随机抽取 50 名学生进行了视力调查，并根据视 力值绘制成统计图（如图），这 50 名学生视力的中位数所在范围是 _______. 12.如图，将分别含有 30°、45° 角的一副三角板重叠，使直角顶点重合，若两直角重叠形成的角为 65°, 则图中角 α 的度数为 ________. 3 7 14 19 7 人数 0 4 8 12 16 20 4.05以下 4.35~4.654.05~4.35 4.65~4.95 4.95以上 视力值 （第11题图） 65° α (第12题图） 30° 60° 90°120° 150° 180° 210° 240° 270° 300° 330° A B C （第13题图） 13.以水平数轴的原点 O 为圆心，过正半轴 Ox 上的每一刻度点画同心圆，将 Ox 逆时针依次旋转 30°、 60°、90°、⋯、330° 得到 11 条射线，构成如图所示的“圆”坐标系，点 A、B 的坐标分别表示为 (5, 0°)、 (4, 300°), 则点 C 的坐标表示为 ________. 14. 如图，直线 a ⊥ b, 垂足为 H, 点 P 在直线 b 上，PH = 4cm，O 为直线 b 上一动点，若以 1cm 为半径 的 ⊙ O 与直线 a 相切，则 OP 的长为 ________. 15. 如图所示的网格由边长为 1 个单位长度的小正方形组成，点 A、B、C、在直角坐标系中的坐标分别 为 (3, 6), (-3, 3), (7, -2), 则 △ ABC 内心的坐标为________. 16. 如图，点 P 在反比例函数 y = 3 x  的图像上，且横坐标为 1，过点 P 作两条坐标轴的平行线，与反比例 函数 y = k x (k < 0) 的图像相交于点 A、B， 则直线 AB 与 x 轴所夹锐角的正切值为_______. a bP O H （第14题图） A B C（第15题图） O x y P （第16题图） 三、解答题（本大题共有 10 题，共 102 分，请在答题卡规定区域内作答，解答时应写出必要的文字说明、 证明过程或演算步骤） 17.( 本题满分 12 分 ) (1) 计算：(-π)0 + ( 1 2 )-1 - 3  sin60°; (2) 解不等式组： 3x - 1 ≥ x + 1, x + 4 < 4x - 2. 18.( 本题满分 8 分 ) 2020 年 6 月 1 日起，公安部在全国开展“一盔一带”安全守护行动.某校小交警社团在交警带领 下，从 5 月 29 日起连续 6 天，在同一时段对某地区一路口的摩托车和电动自行车骑乘人员佩戴头 盔情况进行了调查，并将数据绘制成图表如下： 0 20 40 60 80 100 头盔佩戴率（%） 5.29 5.30 5.31 6.1 6.2 6.3 23 26 40 43 45 46 59 62 78 89 90 95 摩托车 电动 自行车 日期 2020年5月29日~6月3日 骑乘人员头盔佩戴率折线统计图 2020年6月2日 骑乘人员头盔佩戴情况统计表 骑乘 摩托车 骑乘 电动自行车 戴头盔人数 18 72 不戴头盔人数 2 m (1) 根据以上信息，小明认为 6 月 3 日该地区全天摩托车骑乘人员头盔佩戴率约为 95% . 你是否同 意他的观点？请说明理由； (2) 相比较而言，你认为需要对哪类人员加大宣传引导力度？为什么？ (3) 求统计表中 m 的值. 19.( 本题满分 8 分 ) 一只不透明袋子中装有 1 个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸 球试验：将球搅匀后从中任意摸出 1 个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如 下： 摸球的次数 200 300 400 1000 1600 2000 摸到白球的频数 72 93 130 334 532 667 摸到白球的频率 0.3600 0.3100 0.3250 0.3340 0.3325 0.3335 (1) 该学习小组发现，摸到白球的频率在一个常数附近摆动，这个常数是 _______.（精确到 0.01），由此估出红球有 ______ 个. (2) 现从该袋中摸出 2 个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到 1 个 乒乓球，1 个红球的概率. 20.( 本题满分 10 分 ) 近年来，我市大力发展城市快速交通，小王开车从家到单位有两条路线可选择，路线 A 为全程 25km 的普通道路，路线 B 包含快速通道，全程 30km, 走路线 B 比走路线 A 平均速度提高 50%，时 间节省 6min, 求走路线 B 的平均速度. 21.( 本题满分 10 分 ) 如图，已知线段 a, 点 A 在平面直角坐标系 xOy 内， (1) 用直尺和圆规在第一象限内. . . . . 作出点 P，使点 P 到两坐标轴的距离相等，且与点 A 的距离等于 a.( 保留作图痕迹，不写作法 ) (2) 在 (1) 的条件下，若 a ≈ 2 5  , A 点的坐标为 (3, 1), 求 P 点的坐标. a A x y O （第21题图） 22.( 本题满分 10 分 ) 我市在凤城河风景区举办了端午节赛龙舟活动，小亮在河畔的一幢楼上看到一艘龙舟迎面驶 来，他在高出水面 15m 的 A 处测得在 C 处的龙舟俯角为 23°; 他登高 6m 到正上方的 B 处测得驶至 D 处的龙舟俯角为 50°, 问两次观测期间龙舟前进了多少？（结果精确到 1m, 参考数据：tan23° ≈ 0.42, tan40° ≈ 0.84, tan50° ≈ 1.19, tan67° ≈ 2.36) 50° 23°A B CD 水面 （第22题图） 23.( 本题满分 10 分 ) 如图，在 △ ABC 中，∠ C = 90°, AC = 3, BC = 4, P 为 BC 边上的动点（与 B、C 不重合）， PD ⎳ AB, 交 AC 于点 D，连接 AP，设 CP = x, △ ADP 的面积为 S. (1) 用含 x 的代数式表示 AD 的长； (2) 求 S 与 x 的函数表达式，并求当 S 随 x 增大而减小时 x 的取值范围. A BC P D （第23题图） 24.( 本题满分 10 分 ) 如图，在 ⊙ O 中，点 P 为 AB  的中点，弦 AD、PC 互相垂直，垂足为 M ，BC 分别与 AD、PD 相 交于点 E、N ，连接 BD、MN. (1) 求证：N 为 BE 的中点. (2) 若 ⊙ O 的半径为 8，AB  的度数为 90°, 求线段 MN 的长. A B C D E M NO P （第24题图） 25.( 本题满分 12 分 ) 如图，正方形 ABCD 的边长为 6，M 为 AB 的中点， △ MBE 为等边三角形，过点 E 作 ME 的垂 线分别与边 AD、BC 相交于点 F、G，点 P、Q 分别在线段 EF、BC 上运动，且满足 ∠ PMQ = 60°, 连接 PQ. (1) 求证：△ MEP ≌ △ MBQ. (2) 当点 Q 在线段 GC 上时，试判断 PF + GQ 的值是否变化？如果不变，求出这个值，如果变化， 请说明理由. (3) 设 ∠ QMB = α, 点 B 关于 QM 的对称点为 B‘，若点 B’落在 △ MPQ 的内部，试写出 α 的范围， 并说明理由. A B C D E F G M P Q （第25题图） 26.( 本题满分 14 分 ) 如图，二次函数 y1 = a(x - m)2 + n、y2 = 6ax2 + n(a < 0, m > 0, n > 0) 的图像分别为 C1、C2， C1 交 y 轴于点 P，点 A 在 C1 上，且位于 y 轴右侧，直线 PA 与 C2 在 y 轴左侧的交点为 B. (1) 若 P 点的坐标为 (0, 2), C1 的顶点坐标为 (2, 4), 求 a 的值； (2) 设直线 PA 与 y 轴所夹的角为 α. ①当 α = 45°, 且 A 为 C1 的顶点时，求 am 的值； ②若 α = 90°, 试说明：当 a、m、n 各自取不同的值时，PA PB  的值不变； (3) 若 PA = 2PB， 试判断点 A 是否为 C1 的顶点？请说明理由。 O x y A B P C1 C2 (第26题图） O x y A B P C1 C2 （备用图）