2011年上海市中考数学试卷【答案+解析】 18页

2011 年上海市中考数学试卷 一、选择题（本大题共 6 题，每题 4 分，共 24 分） 1．（ 2011•上海）下列分数中，能化为有限小数的是（ ） A． B． C． D． 2．（ 2011•上海）如果 a＞b，c＜0，那么下列不等式成立的是（ ） A．a+c＞b+c B．c﹣a＞c﹣b C．ac＞bc D． 3．（ 2011•上海）下列二次根式中，最简二次根式是（ ） A． B． C． D． 4．（ 2011•上海）抛物线 y=﹣（x+2）2﹣3 的顶点坐标是（ ） A．（ 2，﹣3） B．（﹣2，3） C．（ 2，3） D．（﹣2，﹣3） 5．（ 2011•上海）下列命题中，真命题是（ ） A．周长相等的锐角三角形都全等 B．周长相等的直角三角形都全等 C．周长相等的钝角三角形都全等 D．周长相等的等腰直角三角形都全等 6．（ 2011•上海）矩形 ABCD 中，AB=8， ，点 P 在边 AB 上，且 BP=3AP，如果圆 P 是以点 P 为圆心，PD 为半径的圆，那么下列判断正确的是（ ） A．点 B、C 均在圆 P 外 B．点 B 在圆 P 外、点 C 在圆 P 内 C．点 B 在圆 P 内、点 C 在圆 P 外 D．点 B、 C 均在圆 P 内 二、填空题（本大题共 12 题，每题 4 分，共 48 分） 7．（ 2011•上海）计算：a2•a3= _________ ． 8．（ 2011•上海）因式分解：x2﹣9y2= _________ ． 9．（ 2011•上海）如果关于 x 的方程 x2﹣2x+m=0（m 为常数）有两个相等实数根，那么 m= _________ ． 10．（ 2011•上海）函数 的定义域是 _________ ． 11．（ 2011•上海）如果反比例函数 （k 是常数，k≠0）的图象经过点（﹣1，2），那么这个函数的解析式是 _________ ． 12．（ 2011•上海）一次函数 y=3x﹣2 的函数值 y 随自变量 x 值的增大而 _________ （填“增大”或“减小”）． 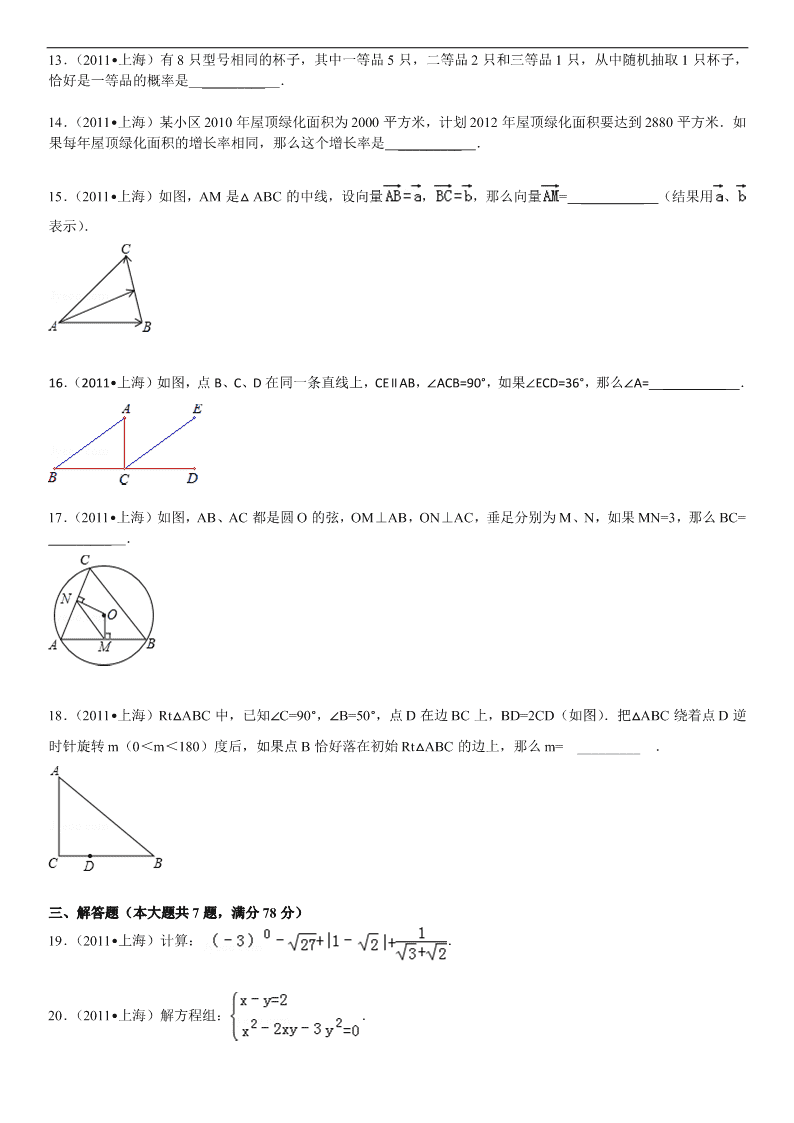13．（ 2011•上海）有 8 只型号相同的杯子，其中一等品 5 只，二等品 2 只和三等品 1 只，从中随机抽取 1 只杯子， 恰好是一等品的概率是 _________ ． 14．（ 2011•上海）某小区 2010 年屋顶绿化面积为 2000 平方米，计划 2012 年屋顶绿化面积要达到 2880 平方米．如 果每年屋顶绿化面积的增长率相同，那么这个增长率是 _________ ． 15．（ 2011•上海）如图，AM 是△ ABC 的中线，设向量 ， ，那么向量 = _________ （结果用 、 表示）． 16．（ 2011•上海）如图，点 B、C、D 在同一条直线上，CE∥AB，∠ACB=90°，如果∠ECD=36°，那么∠A= _________ ． 17．（ 2011•上海）如图，AB、AC 都是圆 O 的弦，OM⊥AB，ON⊥AC，垂足分别为 M、N，如果 MN=3，那么 BC= _________ ． 18．（ 2011•上海）Rt△ABC 中，已知∠C=90°，∠B=50°，点 D 在边 BC 上，BD=2CD（如图）．把△ABC 绕着点 D 逆 时针旋转 m（0＜m＜180）度后，如果点 B 恰好落在初始 Rt△ABC 的边上，那么 m= _________ ． 三、解答题（本大题共 7 题，满分 78 分） 19．（ 2011•上海）计算： ． 20．（ 2011•上海）解方程组： ． 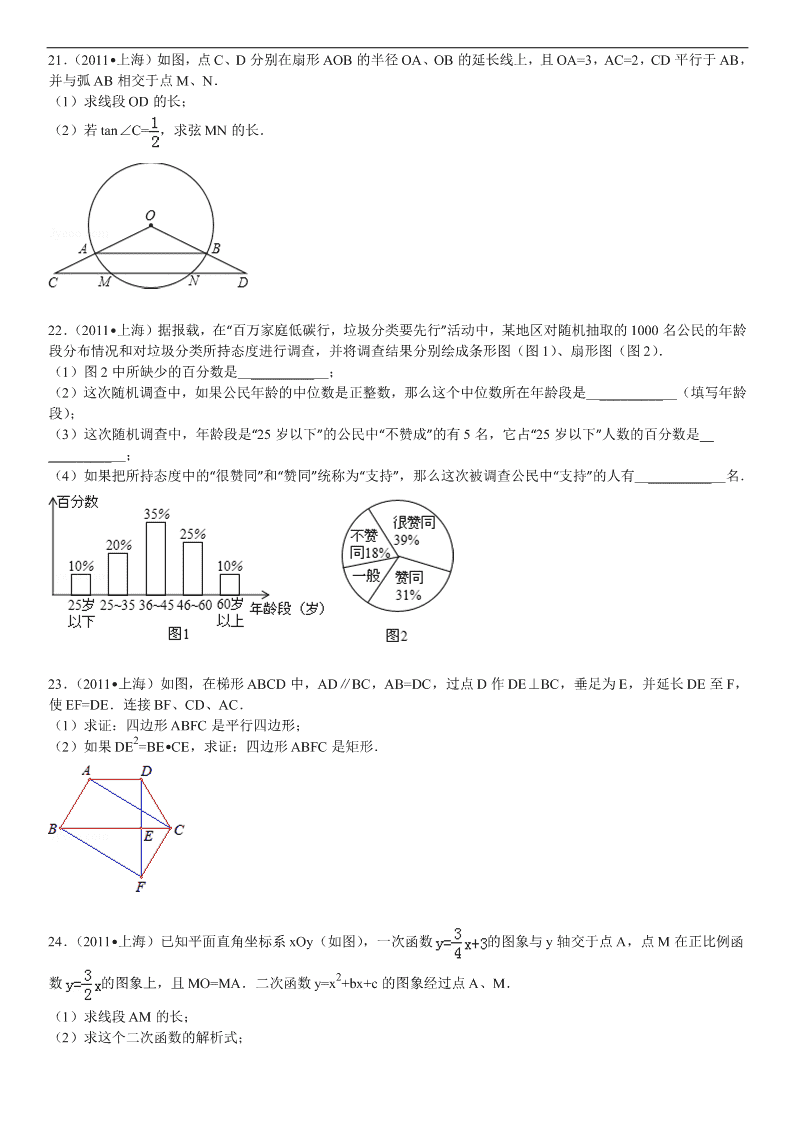21．（ 2011•上海）如图，点 C、D 分别在扇形 AOB 的半径 OA、OB 的延长线上，且 OA=3，AC=2，CD 平行于 AB， 并与弧 AB 相交于点 M、N． （1）求线段 OD 的长； （2）若 tan∠C= ，求弦 MN 的长． 22．（ 2011•上海）据报载，在“百万家庭低碳行，垃圾分类要先行”活动中，某地区对随机抽取的 1000 名公民的年龄 段分布情况和对垃圾分类所持态度进行调查，并将调查结果分别绘成条形图（图 1）、扇形图（图 2）． （1）图 2 中所缺少的百分数是 _________ ； （2）这次随机调查中，如果公民年龄的中位数是正整数，那么这个中位数所在年龄段是 _________ （填写年龄 段）； （3）这次随机调查中，年龄段是“25 岁以下”的公民中“不赞成”的有 5 名，它占“25 岁以下”人数的百分数是 _________ ； （4）如果把所持态度中的“很赞同”和“赞同”统称为“支持”，那么这次被调查公民中“支持”的人有 _________ 名． 23．（ 2011•上海）如图，在梯形 ABCD 中，AD∥BC，AB=DC，过点 D 作 DE⊥BC，垂足为 E，并延长 DE 至 F， 使 EF=DE．连接 BF、CD、AC． （1）求证：四边形 ABFC 是平行四边形； （2）如果 DE2=BE•CE，求证：四边形 ABFC 是矩形． 24．（ 2011•上海）已知平面直角坐标系 xOy（如图），一次函数 的图象与 y 轴交于点 A，点 M 在正比例函 数 的图象上，且 MO=MA．二次函数 y=x2+bx+c 的图象经过点 A、M． （1）求线段 AM 的长； （2）求这个二次函数的解析式； （3）如果点 B 在 y 轴上，且位于点 A 下方，点 C 在上述二次函数的图象上，点 D 在一次函数 的图象上， 且四边形 ABCD 是菱形，求点 C 的坐标． 25．（ 2011•上海）在 Rt△ ABC 中，∠ACB=90°，BC=30，AB=50．点 P 是 AB 边上任意一点，直线 PE⊥AB，与边 AC 或 BC 相交于 E．点 M 在线段 AP 上，点 N 在线段 BP 上，EM=EN， ． （1）如图 1，当点 E 与点 C 重合时，求 CM 的长； （2）如图 2，当点 E 在边 AC 上时，点 E 不与点 A、C 重合，设 AP=x，BN=y，求 y 关于 x 的函数关系式，并写出 函数的定义域； （3）若△ AME∽△ENB（△ AME 的顶点 A、M、E 分别与△ ENB 的顶点 E、N、B 对应），求 AP 的长． 2011 年上海市中考数学试卷 参考答案与试题解析 一、选择题（本大题共 6 题，每题 4 分，共 24 分） 1．（ 2011•上海）下列分数中，能化为有限小数的是（ ） A． B． C． D． 考点：有理数的除法。 专题：计算题。 分析：本题需根据有理数的除法法则分别对每一项进行计算，即可求出结果． 解答：解：A∵ =0.3…故本选项错误； B、∵ =0.2 故本选项正确； C、 =0.142857…故本选项错误； D、 =0.1…故本选项错误． 故选 B． 点评：本题主要考查了有理数的除法，在解题时要根据有理数的除法法则分别计算是解题的关键． 2．（ 2011•上海）如果 a＞b，c＜0，那么下列不等式成立的是（ ） A．a+c＞b+c B．c﹣a＞c﹣b C．ac＞bc D． 考点：不等式的性质。 专题：计算题。 分析：根据不等式的基本性质：（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变．（2）不等式 两边乘（或除以）同一个正数，不等号的方向不变． （3）不等式两边乘（或除以）同一个负数，不等号的方向改变．一个个筛选即可得到答案． 解答：解：A，∵a＞b，∴a+c＞b+c，故此选项正确； B，∵a＞b， ∴﹣a＜﹣b， ∴﹣a+c＜﹣b+c， 故此选项错误； C，∵a＞b，c＜0， ∴ac＜bc， 故此选项错误； D，∵a＞b，c＜0， ∴ ＜ ， 故此选项错误； 故选：A． 点评：此题主要考查了不等式的基本性质．“0”是很特殊的一个数，因此，解答不等式的问题时，应密切关注“0”存 在与否，以防掉进“0”的陷阱，准确把握不等式的性质是做题的关键． 3．（ 2011•上海）下列二次根式中，最简二次根式是（ ） A． B． C． D． 考点：最简二次根式。 专题：计算题。 分析：判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时 满足的就是最简二次根式，否则就不是． 解答：解：A、 = ，被开方数含分母，不是最简二次根式；故此选项错误 B、 = ，被开方数含分母，不是最简二次根式；故此选项错误 C、 ，是最简二次根式；故此选项正确； D. =5 ，被开方数，含能开得尽方的因数或因式，故此选项错误 故选 C． 点评：此题主要考查了最简二次根式的定义．根据最简二次根式的定义，最简二次根式必须满足两个条件：（1）被 开方数不含分母；（2）被开方数不含能开得尽方的因数或因式． 4．（ 2011•上海）抛物线 y=﹣（x+2）2﹣3 的顶点坐标是（ ） A．（ 2，﹣3） B．（﹣2，3） C．（ 2，3） D．（﹣2，﹣3） 考点：二次函数的性质。 专题：计算题。 分析：已知抛物线解析式为顶点式，根据顶点式的坐标特点求顶点坐标． 解答：解：∵抛物线 y=﹣（x+2）2﹣3 为抛物线解析式的顶点式， ∴抛物线顶点坐标是（﹣2，﹣3）． 故选 D． 点评：本题考查了二次函数的性质．抛物线 y=a（x﹣h）2+k 的顶点坐标是（h，k）． 5．（ 2011•上海）下列命题中，真命题是（ ） A．周长相等的锐角三角形都全等 B．周长相等的直角三角形都全等 C．周长相等的钝角三角形都全等 D．周长相等的等腰直角三角形都全等 考点：全等三角形的判定；命题与定理。 专题：证明题。 分析：全等三角形必须是对应角相等，对应边相等，根据全等三角形的判定方法，逐一检验． 解答：解：A、周长相等的锐角三角形的对应角不一定相等，对应边也不一定相等，假命题； B、周长相等的直角三角形对应锐角不一定相等，对应边也不一定相等，假命题； C、周长相等的钝角三角形对应钝角不一定相等，对应边也不一定相等，假命题； D、由于等腰直角三角形三边之比为 1：1： ，故周长相等时，等腰直角三角形的对应角相等，对应边相等，故 全等，真命题． 故选 D． 点评：本题考查了全等三角形的判定定理的运用，命题与定理的概念．关键是明确全等三角形的对应边相等，对应 角相等． 6．（ 2011•上海）矩形 ABCD 中，AB=8， ，点 P 在边 AB 上，且 BP=3AP，如果圆 P 是以点 P 为圆心，PD 为半径的圆，那么下列判断正确的是（ ） A．点 B、C 均在圆 P 外 B．点 B 在圆 P 外、点 C 在圆 P 内 C．点 B 在圆 P 内、点 C 在圆 P 外 D．点 B、 C 均在圆 P 内 考点：点与圆的位置关系。 专题：计算题；数形结合。 分析：根据 BP=3AP 和 AB 的长度求得 AP 的长，然后利用勾股定理求得圆 P 的半径 PD 的长，根据点 B、C 到 P 点的距离判断点 P 与圆的位置关系即可． 解答：解：∵AB=8，点 P 在边 AB 上，且 BP=3AP， ∴AP=2， ∴r=PD= =7， PC= = =9， ∵PB=6＜r，PC=9＞r ∴点 B 在圆 P 内、点 C 在圆 P 外 故选 C． 点评：本题考查了点与圆的位置关系的判定，根据点与圆心之间的距离和圆的半径的大小关系作出判断即可． 二、填空题（本大题共 12 题，每题 4 分，共 48 分） 7．（ 2011•上海）计算：a2•a3= a5 ． 考点：同底数幂的乘法。 分析：根据同底数的幂的乘法，底数不变，指数相加，计算即可． 解答：解：a2•a3=a2+3=a5． 点评：熟练掌握同底数的幂的乘法的运算法则是解题的关键． 8．（ 2011•上海）因式分解：x2﹣9y2= （x+3y）（ x﹣3y） ． 考点：因式分解-运用公式法。 分析：直接利用平方差公式分解即可． 解答：解：x2﹣9y2=（x+3y）（ x﹣3y）． 点评：本题主要考查利用平方差公式分解因式，熟记公式结构是解题的关键． 9．（ 2011•上海）如果关于 x 的方程 x2﹣2x+m=0（m 为常数）有两个相等实数根，那么 m= 1 ． 考点：根的判别式。 专题：计算题。 分析：本题需先根据已知条件列出关于 m 的等式，即可求出 m 的值． 解答：解：∵x 的方程 x2﹣2x+m=0（m 为常数）有两个相等实数根 ∴△=b2﹣4ac=（﹣2）2﹣4×1•m=0 4﹣4m=0 m=1 故答案为：1 点评：本题主要考查了根的判别式，在解题时要注意对根的判别式进行灵活应用是本题的关键． 10．（ 2011•上海）函数 的定义域是 x≤3 ． 考点：函数自变量的取值范围。 专题：计算题。 分析：二次根式有意义，被开方数为非负数，即 3﹣x≥0，解不等式即可． 解答：解：依题意，得 3﹣x≥0， 解得 x≤3． 故答案为：x≤3． 点评：本题考查了函数的自变量取值范围的求法．关键是根据二次根式有意义时，被开方数为非负数建立不等式． 11．（ 2011•上海）如果反比例函数 （k 是常数，k≠0）的图象经过点（﹣1，2），那么这个函数的解析式是 y= ﹣ ． 考点：待定系数法求反比例函数解析式。 专题：待定系数法。 分析：根据图象过（﹣1，2）可知，此点满足关系式，能使关系时左右两边相等． 解答：解：把（﹣1，2）代入反比例函数关系式得：k=﹣2， ∴y=﹣ ， 故答案为：y=﹣ ， 点评：此题主要考查了用待定系数法求反比例函数的解析式，是中学阶段的重点． 12．（ 2011•上海）一次函数 y=3x﹣2 的函数值 y 随自变量 x 值的增大而 增大 （填“增大”或“减小”）． 考点：一次函数的性质。 专题：存在型。 分析：根据一次函数的性质判断出一次函数 y=3x﹣2 中 k 的符号，再根据一次函数的增减性进行解答即可． 解答：解：∵一次函数 y=3x﹣2 中，k=3＞0， ∴函数值 y 随自变量 x 值的增大而增大． 故答案为：增大． 点评：本题考查的是一次函数的性质，即一次函数 y=kx+b（k≠0）中，k＞0 时，y 随 x 的增大而增大． 13．（ 2011•上海）有 8 只型号相同的杯子，其中一等品 5 只，二等品 2 只和三等品 1 只，从中随机抽取 1 只杯子， 恰好是一等品的概率是 ． 考点：概率公式。 专题：应用题。 分析：共有八只型号相同的杯子，每只杯子被抽到的机会是相同的，故可用概率公式解答． 解答：解：在 8 只型号相同的杯子中， 一等品有 5 只， 则从中随机抽取 1 只杯子，恰好是一等品的概率是 P= ． 故答案为 ． 点评：此题考查概率的求法：如果一个事件有 n 种可能，而且这些事件的可能性相同，其中事件 A 出现 m 种结果， 那么事件 A 的概率 P（A）= ． 14．（ 2011•上海）某小区 2010 年屋顶绿化面积为 2000 平方米，计划 2012 年屋顶绿化面积要达到 2880 平方米．如 果每年屋顶绿化面积的增长率相同，那么这个增长率是 20% ． 考点：一元二次方程的应用。 专题：增长率问题。 分析：本题需先设出这个增长率是 x，再根据已知条件找出等量关系列出方程，求出 x 的值，即可得出答案． 解答：解：设这个增长率是 x，根据题意得： 2000×（1+x）2=2880 解得：x1=20%，x2=﹣220%（舍去） 故答案为：20%． 点评：本题主要考查了一元二次方程的应用，在解题时要根据已知条件找出等量关系，列出方程是本题的关键． 15．（ 2011•上海）如图，AM 是△ ABC 的中线，设向量 ， ，那么向量 = + （结果用 、 表 示）． 考点：*平面向量。 专题：数形结合。 分析：首先由 AM 是△ ABC 的中线，即可求得 的长，又由 = + ，即可求得答案． 解答：解：∵AM 是△ ABC 的中线， ， ∴ = = ， ∵ ， ∴ = + = + ． 故答案为： + ． 点评：此题考查了平面向量的知识．题目难度不大，注意数形结合思想的应用． 16．（ 2011•上海）如图，点 B、C、D 在同一条直线上，CE∥AB，∠ACB=90°，如果∠ECD=36°，那么∠A= 54° ． 考点：平行线的性质；三角形内角和定理。 分析：由∠ACB=90°，∠ECD=36°，求得∠ACE 的度数，又由 CE∥AB，即可求得∠A 的度数． 解答：解：∵∠ECD=36°，∠ACB=90°， ∴∠ACD=90°， ∴∠ACE=∠ACD﹣∠ECD=90°﹣36°=54°， ∵CE∥AB， ∴∠A=∠ACE=54°． 故答案为：54°． 点评：此题考查了平行线的性质．解题的关键是注意数形结合思想的应用． 17．（ 2011•上海）如图，AB、AC 都是圆 O 的弦，OM⊥AB，ON⊥AC，垂足分别为 M、N，如果 MN=3，那么 BC= 6 ． 考点：三角形中位线定理；垂径定理。 分析：由 AB、AC 都是圆 O 的弦，OM⊥AB，ON⊥AC，根据垂径定理可知 M、N 为 AB、AC 的中点，线段 MN 为△ ABC 的中位线，根据中位线定理可知 BC=2MN． 解答：解：∵AB、AC 都是圆 O 的弦，OM⊥AB，ON⊥AC， ∴M、N 为 AB、AC 的中点，即线段 MN 为△ ABC 的中位线， ∴BC=2MN=6． 故答案为：6． 点评：本题考查了垂径定理，三角形的中位线定理的运用．关键是由垂径定理得出两个中点． 18．（ 2011•上海）Rt△ ABC 中，已知∠C=90°，∠B=50°，点 D 在边 BC 上，BD=2CD（如图）．把△ ABC 绕着点 D 逆时针旋转 m（0＜m＜180）度后，如果点 B 恰好落在初始 Rt△ ABC 的边上，那么 m= 80°或 120° ． 考点：旋转的性质。 专题：计算题。 分析：本题可以图形的旋转问题转化为点 B 绕 D 点逆时针旋转的问题，故可以 D 点为圆心，DB 长为半径画弧，第 一次与原三角形交于斜边 AB 上的一点 B′，交直角边 AC 于 B″，此时 DB′=DB，DB″=DB=2CD，由等腰三角形的性 质求旋转角∠BDB′的度数，在 Rt△ B″CD 中，解直角三角形求∠CDB″，可得旋转角∠BDB″的度数． 解答：解：如图，在线段 AB 取一点 B′，使 DB=DB′，在线段 AC 取一点 B″，使 DB=DB″， ∴旋转角 m=∠BDB′=180°﹣∠DB′B﹣∠B=180°﹣2∠B=80°， 在 Rt△ B″CD 中，∵DB″=DB=2CD，∴∠CDB″=60°， 旋转角∠BDB″=180°﹣∠CDB″=120°． 故答案为：80°或 120°． 点评：本题考查了旋转的性质．关键是将图形的旋转转化为点的旋转，求旋转角． 三、解答题（本大题共 7 题，满分 78 分） 19．（ 2011•上海）计算： ． 考点：二次根式的混合运算；零指数幂。 专题：计算题。 分析：观察，可以首先去绝对值以及二次根式化简，再合并同类二次根式即可． 解答：解： =1﹣3 + ﹣1+ ， =﹣3 + + ﹣ ， =﹣2 ． 点评：此题主要考查了二次根式的混合运算以及绝对值的性质，在进行此类运算时一般先把二次根式化为最简二次 根式的形式后再运算． 20．（ 2011•上海）解方程组： ． 考点：高次方程。 专题：方程思想。 分析：用代入法即可解答，把①化为 x=1+y，代入②得（1+y）2+2y+3=0 即可． 解答：解： 由①得 y=x﹣2③ 把③代入②，得 x2﹣2x（x﹣2）﹣3（x﹣2）2=0， 即 x2﹣4x+3=0 解这个方程，得 x1=3，x2=1 代入③中，得 或 ． ∴原方程组的解为 或 ． 点评：考查了高次方程，解答此类题目一般用代入法比较简单，先消去一个未知数再解关于另一个未知数的一元二 次方程，把求得结果代入一个较简单的方程中即可． 21．（ 2011•上海）如图，点 C、D 分别在扇形 AOB 的半径 OA、OB 的延长线上，且 OA=3，AC=2，CD 平行于 AB， 并与弧 AB 相交于点 M、N． （1）求线段 OD 的长； （2）若 tan∠C= ，求弦 MN 的长． 考点：垂径定理；勾股定理；相似三角形的判定与性质；解直角三角形。 专题：几何综合题。 分析：（1）根据 CD∥AB 可知，△ OAB∽△OCD，再根据相似三角形的对应边成比例即可求出 OD 的长； （2）过 O 作 OE⊥CD，连接 OM，由垂径定理可知 ME= MN，再根据 tan∠C= 可求出 OE 的长，利用勾股定理 即可求出 ME 的长，进而求出答案． 解答：解：（1）∵CD∥AB，OA=3，AC=2， ∴△OAB∽△OCD， ∴ = ，即 = ， ∴OD=5； （2）过 O 作 OE⊥CD，连接 OM，则 ME= MN， ∵tan∠C= ， ∴设 OE=x，则 CE=2x， 在 Rt△ OEC 中，OC2=OE2+CE2，即 52=x2+（2x）2，解得 x= ， 在 Rt△ OME 中，OM2=OE2+ME2，即 32=（ ）2+ME2，解得 ME=2． ∴MN=4， 故答案为：5；4． 点评：本题考查的是垂径定理，涉及到锐角三角函数的定义、相似三角形的判定与性质及勾股定理，根据题意作出 辅助线是解答此题的关键． 22．（ 2011•上海）据报载，在“百万家庭低碳行，垃圾分类要先行”活动中，某地区对随机抽取的 1000 名公民的年龄 段分布情况和对垃圾分类所持态度进行调查，并将调查结果分别绘成条形图（图 1）、扇形图（图 2）． （1）图 2 中所缺少的百分数是 12% ； （2）这次随机调查中，如果公民年龄的中位数是正整数，那么这个中位数所在年龄段是 36～45 （填写年龄段）； （3）这次随机调查中，年龄段是“25 岁以下”的公民中“不赞成”的有 5 名，它占“25 岁以下”人数的百分数是 5% ； （4）如果把所持态度中的“很赞同”和“赞同”统称为“支持”，那么这次被调查公民中“支持”的人有 700 名． 考点：条形统计图；扇形统计图；中位数。 专题：图表型。 分析：（1）本题需先根据已知条件，再结合图形列出式子，解出结果即可． （2）本题需先根据中位数的概念即可得出答案． （3）本题需先求出 25 岁以下的总人数，再用 5 除以总人数即可得出答案． （4）本题需先求出这次被调查公民中支持的人所占的百分比，再乘以总人数即可得出答案． 解答：解：（1）图 2 中所缺少的百分数是：1﹣39%﹣18%﹣31%=12% （2）这个中位数所在年龄段是：36～45 （3） =5% （4）1000×（39%+31%）=700 故答案为：12%，36～45，5%，700 点评：本题主要考查了条形统计图和扇形统计图的有关知识，在解题时要注意综合利用这两种统计图是本题的关键． 23．（ 2011•上海）如图，在梯形 ABCD 中，AD∥BC，AB=DC，过点 D 作 DE⊥BC，垂足为 E，并延长 DE 至 F， 使 EF=DE．连接 BF、CD、AC． （1）求证：四边形 ABFC 是平行四边形； （2）如果 DE2=BE•CE，求证：四边形 ABFC 是矩形． 考点：等腰梯形的性质；全等三角形的判定与性质；平行四边形的判定与性质；矩形的性质；相似三角形的判定与 性质。 专题：证明题。 分析：（1）连接 BD，利用等腰梯形的性质得到 AC=BD，再根据垂直平分线的性质得到 DB=FB，从而得到 AC=BF， 然后证得 AC∥BF，利用一组对边平行且相等判定平行四边形； （2）利用题目提供的等积式和两直角相等可以证得两直角三角形相似，得到对应角相等，从而得到直角来证明有 一个角是直角的平行四边形是矩形． 解答：证明：（1）连接 BD， ∵梯形 ABCD 中，AD∥BC，AB=DC， ∴AC=BD，∵BC=CB， ∴△ABC≌△DCB， ∴∠ACB=∠DBC ∵DE⊥BC，EF=DE， ∴BD=BF，∠DBC=∠FBC， ∴AC=BF，∠ACB=∠CBF ∴AC∥BF， ∴四边形 ABFC 是平行四边形； （2）∵DE2=BE•CE ∴ ， ∵∠DEB=∠DEC=90°， ∴△BDE∽△DEC， ∴∠CDE=∠DBE， ∴∠BFC=∠BDC=∠BDE+∠CDE=∠BDE+∠DBE=90°， ∴四边形 ABFC 是矩形． 点评：本题考查了等腰梯形的性质、全等及相似三角形的判定及性质等，是一道集合了好几个知识点的综合题，但 题目的难度不算大． 24．（ 2011•上海）已知平面直角坐标系 xOy（如图），一次函数 的图象与 y 轴交于点 A，点 M 在正比例函 数 的图象上，且 MO=MA．二次函数 y=x2+bx+c 的图象经过点 A、M． （1）求线段 AM 的长； （2）求这个二次函数的解析式； （3）如果点 B 在 y 轴上，且位于点 A 下方，点 C 在上述二次函数的图象上，点 D 在一次函数 的图象上， 且四边形 ABCD 是菱形，求点 C 的坐标． 考点：二次函数综合题。 专题：压轴题。 分析：（1）先求出根据 OA 垂直平分线上的解析式，再根据两点的距离公式求出线段 AM 的长； （2）二次函数 y=x2+bx+c 的图象经过点 A、M．待定系数法即可求出二次函数的解析式； （3）可设 D（n， n+3），根据菱形的性质得出 C（n，n2_ n+3）且点 C 在二次函数 y=x2_ x+3 上，得到方程求 解即可． 解答：解：（1）在一次函数 y= x+3 中， 当 x=0 时，y=3． ∴A（0，3）． ∵MO=MA， ∴M 为 OA 垂直平分线上的点， 可求 OA 垂直平分线上的解析式为 y= ， 又∵点 M 在正比例函数 ， ∴M（1， ）， 又∵A（0，3）． ∴AM= ； （2）∵二次函数 y=x2+bx+c 的图象经过点 A、M．可得 ， 解得 ， ∴y=x2﹣ x+3； （3）∵点 D 在一次函数 的图象上， 则可设 D（n， n+3）， 设 B（0，m），（ m＜3）， C（n，n2﹣ n+3） ∵四边形 ABDC 是菱形， ∴|AB|=3﹣m，|DC|=yD﹣yC= n+3﹣（n2_ n+3）= n﹣n2， |AD|= = n， ∵|AB|=|DC|， ∴3﹣m= n﹣n2，①， ∵|AB|=|DA|， ∴3﹣m= n，② 解①②得，n1=0（舍去），n2=2， 将 n=2，代入 C（n，n2_ n+3） ∴C（2，2）． 点评：本题是二次函数的综合题型，其中涉及的知识点有抛物线解析式的确定，两点的距离公式，菱形的性质，解 二元一次方程，综合性较强，难度较大． 25．（ 2011•上海）在 Rt△ ABC 中，∠ACB=90°，BC=30，AB=50．点 P 是 AB 边上任意一点，直线 PE⊥AB，与边 AC 或 BC 相交于 E．点 M 在线段 AP 上，点 N 在线段 BP 上，EM=EN， ． （1）如图 1，当点 E 与点 C 重合时，求 CM 的长； （2）如图 2，当点 E 在边 AC 上时，点 E 不与点 A、C 重合，设 AP=x，BN=y，求 y 关于 x 的函数关系式，并写出 函数的定义域； （3）若△ AME∽△ENB（△ AME 的顶点 A、M、E 分别与△ ENB 的顶点 E、N、B 对应），求 AP 的长． 考点：相似三角形的判定与性质；勾股定理；解直角三角形。 专题：几何综合题。 分析：（1）本题需先根据已知条件得出 AC 的值，再根据 CP⊥AB 求出 CP，从而得出 CM 的值． （2）本题需先根据 EN ，设出 EP 的值，从而得出 EM 和 PM 的值，再得出△ AEP∽△ABC，即可求 出 = ，求出 a 的值，即可得出 y 关于 x 的函数关系式，并且能求出函数的定义域． （3）本题需先设 EP 的值，得出则 EM 和 MP 的值，然后分①点 E 在 AC 上时，根据△ AEP∽△ABC，求出 AP 的 值，从而得出 AM 和 BN 的值，再根据△ AME∽△ENB，求出 a 的值，得出 AP 的长；②点 E 在 BC 上时，根据 △ EBP∽△ABCC，求出 AP 的值，从而得出 AM 和 BN 的值，再根据△ AME∽△ENB，求出 a 的值，得出 AP 的长． 解答：解：（1）∵∠ACB=90°， ∴AC= ， = ， =40， ∵CP⊥AB， ∴ = ， ∴ = ， ∴CP=24， ∴CM= ， = ， =26； （2）∵ ， ∴设 EP=12a， 则 EM=13a，PM=5a， ∵EM=EN， ∴EN=13a，PN=5a， ∵△AEP∽△ABC， ∴ = ， ∴ ， ∴x=16a， ∴a= ， ∴BP=50﹣16a， ∴y=50﹣21a， =50﹣21× ， =50﹣ x， ∵当 E 点与 A 点重合时，x=0．当 E 点与 C 点重合时，x=32． ∴函数的定义域是：（0＜x＜32）； （3）①当点 E 在 AC 上时，如图 2，设 EP=12a，则 EM=13a，MP=NP=5a， ∵△AEP∽△ABC， ∴ ， ∴ ， ∴AP=16a， ∴AM=11a， ∴BN=50﹣16a﹣5a=50﹣21a， ∵△AME∽△ENB， ∴ ， ∴ = ， ∴a= ， ∴AP=16× =22， ②当点 E 在 BC 上时，如图（备用图），设 EP=12a，则 EM=13a，MP=NP=5a， ∵△EBP∽△ABC， ∴ = ， 即 = ， 解得 BP=9a， ∴BN=9a﹣5a=4a，AM=50﹣9a﹣5a=50﹣14a， ∵△AME∽△ENB， ∴ ， 即 = ， 解得 a= ， ∴AP=50﹣9a=50﹣9× =42． 所以 AP 的长为：22 或 42． 点评：本题主要考查了相似三角形、勾股定理、解直角三角形的判定和性质，在解题时要注意知识的综合应是解本 题的关键． 参与本试卷答题和审题的老师有： lantin；nhx600；zhangCF；sd2011；gbl210；CJX；HJJ；sjzx；HLing；zhjh；zcx；ZJX。（排名不分先后） 菁优网 2012 年 5 月 27 日