人教版九年级数学上册单元测试题 52页

人教版九年级数学上册单元测试题 第二十一章检测题(R) (时间：120 分钟　　满分：120 分) 一、选择题(本大题共 10 小题，每小题 3 分，共 30 分) 1．下列方程中是关于 x 的一元二次方程的是（ C ） A．x2＋3 x ＝0　　 　　　　　　　B．y2－2x＋1＝0　 C．x2－5x＝2 D．x2－2＝(x＋1)2 2．用直接开平方法解下列一元二次方程，其中无解的方程为（ C ） A．x2－1＝0 B．x2＝0 C．x2＋4＝0 D．－x2＋3＝0 3．方程 x2－2(x＋3)(x－4)＝10 化成一般形式为(　A　) A．x2－2x－14＝0 B．x2＋2x＋14＝0 C．x2＋2x－14＝0 D．x2－2x＋14＝0 4．下列方程采用配方法求解较简便的是( B ) A．3x2＋x－1＝0 B．4x2－4x－5＝0 C．x2－7x＝0 D．(x－3)2＝4x2 5．一元二次方程 3x2－4x＋1＝0 的根的情况为（ D ） A．没有实数根 B．只有一个实数根 C．有两个相等的实数根 D．有两个不相等的实数根 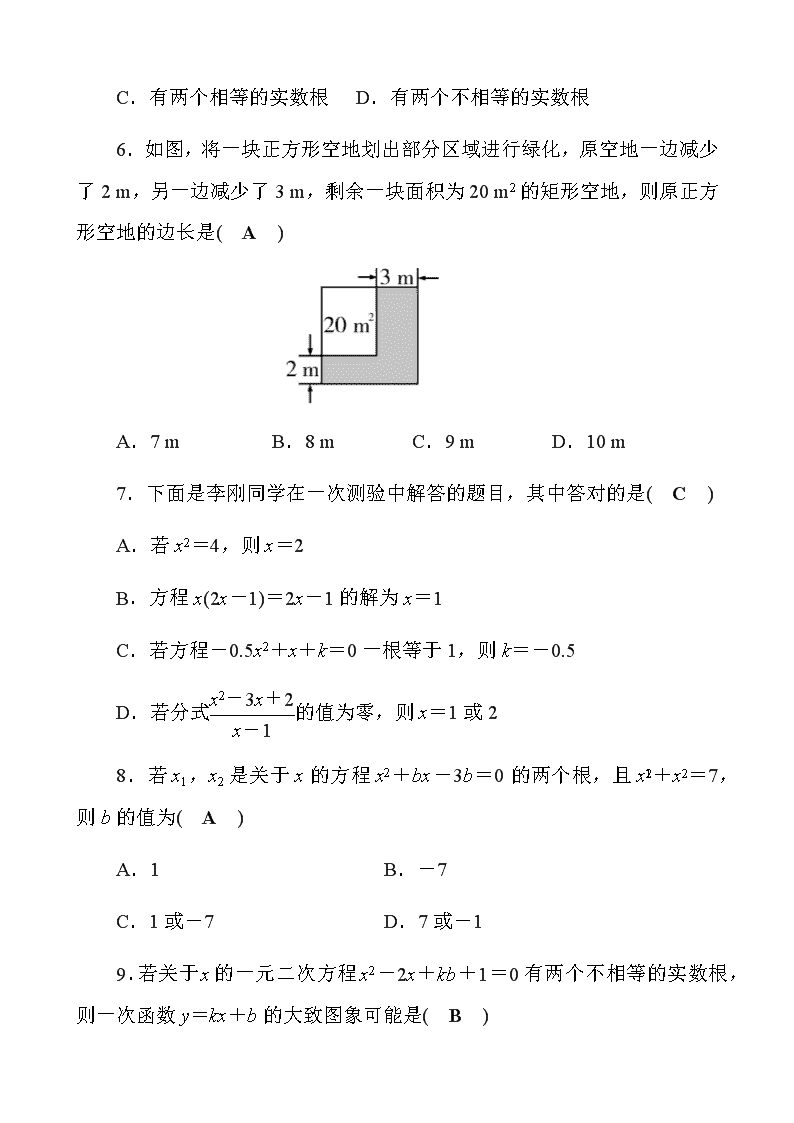6．如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少 了 2 m，另一边减少了 3 m，剩余一块面积为 20 m2 的矩形空地，则原正方 形空地的边长是(　A　) A．7 m B．8 m C．9 m D．10 m 7．下面是李刚同学在一次测验中解答的题目，其中答对的是( C ) A．若 x2＝4，则 x＝2 B．方程 x(2x－1)＝2x－1 的解为 x＝1 C．若方程－0.5x2＋x＋k＝0 一根等于 1，则 k＝－0.5 D．若分式x2－3x＋2 x－1 的值为零，则 x＝1 或 2 8．若 x1，x2 是关于 x 的方程 x2＋bx－3b＝0 的两个根，且 x 21＋x22＝7， 则 b 的值为(　A　) A．1 B．－7 C．1 或－7 D．7 或－1 9．若关于x 的一元二次方程x 2－2x＋kb＋1＝0有两个不相等的实数根， 则一次函数 y＝kx＋b 的大致图象可能是( B ) 10．当 m<－2 时，关于 x，y 的方程组{x＝my， y2－x＋1＝0的实数解的个数是 （ C ） A．0 个 B．1 个 C．2 个 D．3 个 二、填空题(本大题共 8 小题，每小题 3 分，共 24 分) 11．已知实数 x1，x2 满足 x1＋x2＝7，x1x2＝12，则以 x1，x2 为根的一 元二次方程是 x2－7x＋12＝0. 12．已知方程 x2－3x＋k＝0 的一个根为 x＝2，则 k＝ 2 . 13．已知关于 x 的一元二次方程 x2＋bx＋b－1＝0 有两个相等的实数 根，则 b 的值是 2 . 14．已知 b，c 为实数，且满足(b－c－1)2＝－ b＋1，则一元二次方程 x2＋bx＋c＝0 的根为 x1＝－1，x2＝2. 15．已知实数 m，n 满足 3m2＋6m－5＝0，3n 2＋6n－5＝0，且 m≠n， 则 m2＋n2＝ 22 3 . 16．关于 x 的一元二次方程(m－3)xm2－5m＋8＋(m－2)x＋5＝0 的解 为 x＝± 5. 17．三角形的两边长分别是 3 和 4，第三边长是方程 x2－13x＋40＝0 的根，则该三角形的周长为__12__． 18．如图，在矩形 ABCD 中，AB＝6 cm，BC＝8 cm.现有两个动点 P，Q 分别从点 A 和点 B 同时出发，其中点 P 以 1 cm/s 的速度沿 AB 向终点 B 移动，点 Q 以 2 cm/s 的速度沿 BC 向终点 C 移动，其中一点到达终点， 另一点也随之停止运动．连接 PQ，若经过 x s 后 P，Q 两点之间的距离 为 4 2，那么 x 的值为 2 或2 5 . 三、解答题(本大题共 7 小题，共 66 分) 19．(8 分)用适当的方法解下列方程： (1)4x2＋8x＋1＝0； 解：原方程可化为 x2＋2x＋1 4 ＝0，配方，得(x＋1)2＝3 4 ， 开平方，得 x＋1＝± 3 2 ，∴x1＝－1＋ 3 2 ，x2＝－1－ 3 2 . (2)(3t＋2)2＝6t＋4. 解：去括号，得 9t2＋12t＋4＝6t＋4，整理，得 9t2＋6t＝0， ∴3t(3t＋2)＝0，∴t1＝－2 3 ，t2＝0. 20．(8 分)若关于 x 的一元二次方程 ax2＝b(ab＞0)的两个根分别是 m＋1 与 2m－4，求b a 的值． 解：方程 ax2＝b 可变形为 x2＝b a (ab＞ 0)， ∴x＝± b a ， ∴方程的两个根互为相反数， ∴m＋1＋2m－4＝0，解得 m＝1， ∴一元二次方程 ax2＝b(ab＞ 0)的两个根分别是 2 与－2， ∴ b a ＝2，∴b a ＝4. 21.(8 分)随着国家“惠民政策”的陆续出台，为了切实让老百姓得到 实惠，国家卫计委严打药品销售环节中的不正当行为，某种药品原价 200 元/瓶，经过连续两次降价后，现在仅卖 98 元/瓶．现假定两次降价的百分 率相同，求该种药品平均每次降价的百分率． 解：设该种药品平均每次降价的百分率是 x， 由题意得 200(1－x)2＝98. 解得 x1＝1.7(不合题意，舍去)， x2＝0.3＝30%. 答：该种药品平均每次降价的百分率是 30%. 22．(8 分)一元二次方程 x2－2x－5 4 ＝0 的某个根，也是一元二次方程 x2－ (k＋2)x＋9 4 ＝0 的根，求 k 的值． 解：由 x2－2x－5 4 ＝0 得(x－1)2＝9 4 .解得 x1＝5 2 ，x2＝－1 2 . 当 x＝5 2 时，(5 2 )2 －5 2 (k＋2)＋9 4 ＝0，∴k＝7 5 . 当 x＝－1 2 时，(－1 2 )2 ＋1 2 (k＋2)＋9 4 ＝0，∴k＝－7. 又由 Δ＝[－(k＋2)]2－4× 9 4 ≥0，得 k≥1 或 k≤－5， ∴k 的取值符合． ∴k 的值为7 5 或－7. 23.(10 分)已知关于 x 的一元二次方程 x2－2kx＋k2＋2＝2(1－x)有两个 实数根 x1，x2. (1)求实数 k 的取值范围； (2)若方程的两个实数根 x1，x2 满足|x1＋x2|＝x1x2－1，求 k 的值． 解：(1)整理，得 x2－2(k－1)x＋k 2＝0，由题意，得 Δ＝4(k－1) 2－ 4k2≥0.解得 k≤1 2 ； (2)根据根与系数的关系，得 x1＋x2＝2(k－1)，x1x2＝k2， ∵|x1＋x2|＝x1x2－1，∴|2(k－1)|＝k2－1，又∵k≤1 2 ， ∴－2(k－1)＝k2－1 整理，得 k2＋2k－3＝0， 解得 k1＝－3，k2＝1(舍去)，∴k＝－3. 24．(12 分)阅读材料，回答问题． 材料：为解方程 x4－x2－6＝0，可将方程变形为(x2)2－x2－6＝0，然后 设 x2＝y，则(x2)2＝y2，原方程化为 y2－y－6＝0①， 解得 y1＝－2，y2＝3. 当 y1＝－2 时，x2＝－2 无意义，舍去； 当 y2＝3 时，x2＝3，解得 x＝± 3. 所以原方程的解为 x1＝ 3，x2＝－ 3. 问题： (1)在由原方程得到方程①的过程中，利用________法达到了降次的目 的，体现了________的数学思想； (2)利用本题的解题方法，解方程(x2－x)2－4(x2－x)－12＝0. 解：(1)换元，转化 (2)令 x2－x＝y，则原方程可化为 y2－4y－12＝0，即(y＋2)(y－6)＝0， 所以 y＋2＝0 或 y－6＝0，解得 y1＝－2，y2＝6， 当 y1＝－2 时，x2－x＝－2，即 x2－x＋2＝0，此方程无实数根； 当 y2＝6 时，x2－x＝6，(x＋2)(x－3)＝0，解得 x1＝－2，x2＝3，所以 原方程的解为 x1＝－2，x2＝3. 25．(12 分)如图①，为美化校园环境，某校计划在一块长为 100 米， 宽为 60 米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地 修建成同样宽的通道，设通道宽为 a 米． (1)用含 a 的式子表示花圃的面积； (2)如果通道所占面积是整个长方形空地面积的1 4 ，求出此时通道的宽； (3)已知某园林公司修建通道的单价是 50 元/米 2，修建花圃的造价 y(元) 与花圃的修建面积 S(m2)之间的函数关系如图②所示，并且通道宽 a(米)的 值能使关于 x 的方程 1 4 x2－ax＋25a－150＝0 有两个相等的实根，并要求修 建的通道的宽度不少于 5 米且不超过 12 米，如果学校决定由该公司承建此 项目，请求出修建的通道和花圃的造价和为多少元？ 解：(1)由图可知，花圃的面积为(100－2a)(60－2a)＝4a 2－320a＋6 000. (2)由已知可列式：100×60－(100－2a)(60－2a)＝1 4 ×100×60，解得 a1 ＝5，a2＝75(舍去)，∴通道的宽为 5 米． (3)∵方程 1 4 x2－ax＋25a－150＝0 有两个相等的实根，∴Δ＝a2－25a＋150 ＝0.解得 a1＝10，a2＝15.∵5≤a≤12，∴a＝10.设修建的花圃的造价为每 平方米 y 元，y＝55.625S.当 a＝10 时，S花圃＝80×40＝3 200 m2，y 花圃＝3 200× 55.625＝178 000 元，S 通道＝100× 60－80× 40＝2 800 m2，y 通道＝2 800×50＝140 000 元，造价和：178 000＋140 000＝318 000 元． 九上数学第二十二章检测题(R) (时间：120 分钟　　满分：120 分) 一、选择题(本大题共 10 小题，每小题 3 分，共 30 分) 1．下列函数中，不是二次函数的是(　C　) A．y＝2(x－1)2＋4 B．y＝1 2 (x＋1)(x－2) C．y＝x(x＋1)－x2 D．y＝1－ 2x2 2．抛物线 y＝2(x＋m)2＋n(m，n 是常数)的顶点坐标是(　B　) A．(m，n) B．(－m，n) C．(m，－n) D．(－m，－n) 3．(丽水中考)将函数 y＝x2 的图象用下列方法平移后，所得的图象不 经过点 A(1，4)的方法是(　D　) A．向左平移 1 个单位长度 B．向右平移 3 个单位长度 C．向上平移 3 个单位长度 D．向下平移 1 个单位长度 4．二次函数 y＝ax2＋bx－1(a≠0)的图象经过点(1，1)，则 1－a－b 的 值为（ B ） A．－3 B．－1 C．2 D．5 5．已知函数 y＝3x 2－6x＋k(k 为常数)的图象经过点 A(0.8，y 1)， B(1.1，y2)，C( 2，y3)，则有(　C　) A．y1＜y2＜y3 B．y1＞y2＞y3 C．y3＞y1＞y2 D．y1＞y3＞y2 6．已知函数 y＝kx2－7x－7 的图象和 x 轴有交点，则 k 的取值范围是 （ C ） A．k>－7 4 B．k>－7 4 且 k≠0 C．k≥－7 4 D．k≥－7 4 且 k≠0 7．向空中发射一枚炮弹，经 x 秒后的高度为 y 米，且时间与高度的关 系为 y＝ax2＋bx＋c(a≠0)．若此炮弹在第 7 秒与第 14 秒时的高度相等，则 在下列时间中炮弹所在高度最高的是（ B ） A．第 8 秒 B．第 10 秒 C．第 12 秒 D．第 15 秒 8．(泰安中考)在同一坐标系内，一次函数 y＝ax＋b 与二次函数 y＝ax2 ＋8x＋b 的图象可能是图中的（ C ） 9．(2018·黄冈)当 a≤x≤a＋1 时，函数 y＝x 2－2x＋1 的最小值为 1， 则 a 的值为( D ) A．－1 B．2 C．0 或 2 D．－1 或 2 10．(2018·鄂州)如图，抛物线 y＝ax 2＋bx＋c(a≠0)与 x 轴交于点 A(1， 0)和 B，与 y 轴的正半轴交于点 C.有下列结论： ①abc>0；②4a－2b＋c>0；③2a－b>0；④3a＋c>0.其中正确结论的个 数为( B ) A．1 个 B．2 个 C．3 个 D．4 个 　　　 　　　 第 10 题图　　　第 12 题图　　　　第 18 题图 二、填空题(本大题共 8 小题，每小题 3 分，共 24 分) 11．(上海中考)已知一个二次函数的图象开口向上，顶点坐标为(0，－ 1)，那么这个二次函数的解析式可以是 y＝x2－1.(只需写一个) 12．(衡阳中考)已知二次函数 y＝－x2＋3x＋m 的部分图象如图所示， 则关于 x 的一元二次方程－x2＋3x＋m＝0 的解为 x1＝－1，x2＝4. 13．若抛物线 y＝－x2＋8x－12 的顶点是 P，与 x 轴的两个交点是 C，D 两点，则△PCD 的面积是__8__． 14．(原创题)军事演习在平坦的草原上进行，一门迫击炮发射的一发 炮弹飞行的高度 y(m)与飞行时间 x(s)的关系满足 y＝－1 5 x2＋10x，经过 25s 时间，炮弹到达它的最高点，最高点的高度是 125m，经过 50s 时间，炮弹 落到地上爆炸了． 15．已知二次函数 y＝ax2＋bx－3 自变量 x 的部分取值和对应函数值 y 如下表： x … －2 －1 0 1 2 3 … y … 5 0 －3 －4 －3 0 … 则在实数范围内能使得 y－5>0 成立的 x 的取值范围是 x<－2 或 x>4. 16．已知两点 A(－5，y1)，B(3，y2)均在抛物线 y＝ax2＋bx＋c(a≠0)上， 点 C(x0，y0)是该抛物线的顶点．若 y1>y2≥y0，则 x0 的取值范围是 x0>－1. 17．已知二次函数的图象经过原点及点(－1 2 ，－1 4)，且图象与 x 轴的另 一交点到原点的距离为 1，则该二次函数的解析式为 y＝－1 3 x2＋1 3 x 或 y＝x2＋x. 18．二次函数 y＝x2－2x－3 的图象如图所示，若线段 AB 在 x 轴上， 且 AB 为 2 3个单位长度，以 AB 为边作等边△ABC，使点 C 落在该函数 y 轴右侧的图象上，则点 C 的坐标为(1＋ 7，3)或(2，－3)． 三、解答题(本大题共 7 小题，共 66 分) 19．(8 分)已知函数 y＝(m＋3)xm2＋2m－6 是关于 x 的二次函数． (1)求满足条件的 m 的值； (2)当 m 为何值时，抛物线有最低点？求出这个最低点，并求当 x 为何 值时，y 随 x 的增大而增大？ 解：(1)由题意得{m2＋2m－6＝2， m＋3 ≠ 0， 解得{m＝2 或－4， m ≠ －3， 则 m＝2 或－4； (2)当 m＝2 时，抛物线有最低点，为(0，0)， 当 x＞ 0 时，y 随 x 的增大而增大． 20．(8 分)(1)已知抛物线的对称轴是 y 轴，顶点坐标是(0，2)，且经过　 (1，3)，求此抛物线； (2)已知抛物线 y＝ax2＋bx＋c 与 x 轴交于点 A(1，0)，B(3，0)，且过点 C(0，－3)．求抛物线的解析式． 解：(1)由题意设抛物线解析式为 y＝ax2＋k.将(0，2)，(1，3)代入 y＝ ax2＋k，得{k＝2， a＋k＝3，解得{k＝2， a＝1. ∴抛物线解析式为 y＝x2＋2. (2)∵抛物线与 x 轴交于点 A(1，0)，B(3，0)，∴可设抛物线解析式为 y＝a(x－1)(x－3)，把 C(0，－3)代入得 3a＝－3，解得 a＝－1，故抛物线 解析式为 y＝－(x－1)(x－3)，即 y＝－x2＋4x－3. 21．(8 分)如图，已知抛物线 y＝x2－6x＋8 与 x 轴交于 A，B 两点， 与 y 轴交于点 C. (1)求△ABC 的周长； (2)求△ABC 的面积． 解：(1)设 y＝0 得 x2－6x＋8＝0，解得 x1＝2，x2＝4.∴A(2，0)，B(4， 0)，OA＝2，OB＝4，AB＝2. ∵当 x＝0 时，y＝8，∴C(0，8)，OC＝8. 在 Rt△OAC 中，AC＝ OC2＋OA2＝ 82＋22＝2 17； 在 Rt△OBC 中，BC＝ OC2＋OB2＝ 82＋42＝4 5； ∴△ABC 的周长为 2＋4 5＋2 17. (2)S△ABC＝1 2 × 2× 8＝8. 22．(8 分)如图，足球场上守门员在 O 处开出一高球，球从离地面 1 米的 A 处飞出(A 在 y 轴上)，运动员乙在距 O 点 6 米的 B 处发现球在自己 头的正上方达到最高点 M，距地面约 4 米高，球落地后又一次弹起．据实 验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高 度减少到原来最大高度的一半． (1)求足球开始飞出到第一次落地时，该抛物线的解析式； (2)足球第一次落地点 C 距守门员多少米？(取 4 3≈7) (3)运动员乙要抢到第二个落点 D，他应再向前跑多少米？(取 2 6≈5) 解：(1)设足球开始飞出到第一次落地时，抛物线的解析式为 y＝a(x－ 6)2＋4，由题意得当 x＝0 时 y＝1，即 1＝36a＋4，∴a＝－ 1 12 ，∴解析式 为 y＝－ 1 12 (x－6)2＋4. (2)令 y＝0，－ 1 12 (x－6) 2＋4＝0，∴(x－6) 2＝48，解得 x 1＝4 3＋ 6≈13，x2＝－4 3＋6<0(舍去)，∴足球第一次落地距守门员约 13 米． (3)第二次足球弹出后的距离为 CD，根据题意：CD＝EF(即相当于将 抛物线 AEMFC 向下平移了 2 个单位)， ∴2＝－ 1 12 (x－6)2＋4，解得 x1＝6－2 6，x2＝6＋2 6， ∴CD＝|x1－x2|＝4 6≈10，∴BD＝13－6＋10＝17(米)．即运动员乙 应再向前跑 17 米． 23．(10 分)(2018·杭州)设二次函数 y＝ax2＋bx－(a＋b)(a，b 是常数， a≠0)． (1)判断该二次函数图象与 x 轴的交点的个数，并说明理由； (2)若该二次函数图象经过 A(－1，4)，B(0，－1)，C(1，1)三个点中的 其中两个点，求该二次函数的解析式； (3)若 a＋b<0，点 P(2，m)(m>0)在该二次函数图象上，求证：a>0. (1)解：当 y＝0 时，ax2＋bx－(a＋b)＝0(a≠0)， 因为 Δ＝b2＋4a(a＋b)＝(2a＋b)2， 所以当 2a＋b＝0，即 Δ＝0 时二次函数图象与 x 轴有 1 个交点； 当 2a＋b≠0，即 Δ>0 时，二次函数图象与 x 轴有 2 个交点． (2)解：当 x＝1 时，y＝0， 所以函数图象不可能经过点 C(1，1)． 所以函数图象经过 A(－1，4)，B(0，－1)两点， 所以{a－b－（a＋b）＝4， －（a＋b）＝－1. 解得 a＝3，b＝－2. 所以二次函数的解析式为 y＝3x2－2x－1. (3)证明：因为 P(2，m)在该二次函数图象上， 所以 m＝4a＋2b－(a＋b)＝3a＋b， 因为 m>0，所以 3a＋b>0， 又因为 a＋b<0， 所以 2a＝3a＋b－(a＋b)>0， 所以 a>0. 24．(12 分)(2018·扬州)“扬州漆器”名扬天下，某网店专门销售某种 品牌的漆器笔筒，成本为 30 元/件，每天销售量 y(件)与销售单价 x(元)之间 存在一次函数关系，如图所示． (1)求 y 与 x 之间的函数关系式； (2)如果规定每天漆器笔筒的销售量不低于 240 件，当销售单价为多少 元时，每天获取的利润最大，最大利润是多少？ (3)该网店店主热心公益事业，决定从每天的销售利润中捐出 150 元给 希望工程，为了保证捐款后每天剩余利润不低于 3 600 元，试确定该漆器 笔筒销售单价的范围． 解：(1)设 y＝kx＋b，将(40，300)，(55，150)代入，得{40k＋b＝300， 55k＋b＝150， 解得{k＝－10， b＝700； ∴y＝－10x＋700； (2)设每天获得的利润为 w 元， ∴w＝(x－30)·y＝(x－30)(－10x＋700) ＝－10x2＋1 000x－21 000 ＝－10(x－50)2＋4 000. ∵y≥240，∴－10x＋700≥240，解得 x≤46. 又∵－10<0，∴当 x<50 时，w 随 x 的增大而增大． ∴当 x＝46 时，wmax＝3 840(元)． 答：当销售单价为 46 元时，每天获取的利润最大，为 3 840 元． (3)设捐款后每天获取的利润为 W 元，则 W＝w－150＝－10x2＋1 000x －21 150，令 W＝3 600，即－10x2＋1 000x－21 150＝3 600，解得 x1＝55， x2＝45，∵W 关于 x 的函数图象是抛物线的一部分，且开口向下，故当 45≤x≤55 时，捐款后每天剩余利润不低于 3 600 元． 25．(12 分)(2018·菏泽)如图，在平面直角坐标系中，抛物线 y＝ax2＋bx －5 交 y 轴于点 A，交 x 轴于点 B(－5，0)和点 C(1，0)，过点 A 作 AD∥x 轴交抛物线于点 D. (1)求抛物线的解析式； (2)点 E 是抛物线上一点，且点 E 关于 x 轴的对称点在直线 AD 上，求 △ADE 的面积； (3)若点 P 是直线 AB 下方的抛物线上一动点，当点 P 运动到某一位置 时，△ABP 的面积最大，求出此时点 P 的坐标和△ABP 的最大面积． 解：(1)∵抛物线 y＝ax2＋bx－5 经过点 B(－5，0)和 C(1，0)， ∴{25a－5b－5＝0， a＋b－5＝0， 解得{a＝1， b＝4. ∴抛物线的解析式为 y＝x2＋4x－5. (2)∵抛物线 y＝x2＋4x－5 交 y 轴于点 A， ∴A 点坐标为(0，－5)． 又∵点 E 关于 x 轴的对称点在直线 AD 上， ∴点 E 的纵坐标为 5. 过点 E 作 EF⊥DA 的延长线于点 F， ∴EF＝5＋|－5|＝10. 设点 D 的坐标为(m，－5)， ∴m2＋4m－5＝－5，∴m1＝0，m2＝－4， ∴点 D 的坐标为(－4，－5)． ∴AD＝|－4|＝4， ∴S△ADE＝1 2 AD·EF＝1 2 × 4× 10＝20. (3)设直线 AB 的解析式为 y＝kx＋n， ∵直线经过点 B(－5，0)和 A(0，－5)， ∴{－5k＋n＝0， n＝－5， 解得{k＝－1， n＝－5. ∴直线 AB 的解析式为 y＝－x－5. 设点 P 的坐标为(t，t2＋4t－5)．当 x＝t 时，y＝－t－5. ∵OB＝5，∴△ABP 的面积是 S＝1 2 [(－t－5)－(t2＋4t－5)]×5 ＝－5 2(t＋5 2)2 ＋125 8 . ∵a＝－5 2 <0，∴抛物线开口向下．∴当 x＝－5 2 时，△ABP 的面积最大， 此时点 P 的坐标为(－5 2 ，－35 4 )，△ABP 的面积为125 8 . 　　　　　 九上数学第二十三章检测题(R) (时间：120 分钟　　满分：120 分) 一、选择题(本大题共 10 小题，每小题 3 分，共 30 分) 1．下列运动属于旋转的是( D ) A．滚动过程中的篮球 B．一个图形沿某直线对折过程 C．气球升空的运动 D．钟表钟摆的摆动 2．(无锡中考)下列图形中，是中心对称图形的是( C ) 3．如图，在 Rt△ABC 中，∠BAC＝90°，将 Rt△ABC 绕点 C 按逆时针 方向旋转 48°得到 Rt△A′B′C，点 A 在边 B′C 上，则∠B′的大小为（ A ） A．42°　　　　　B．48°　　　　　C．52°　　　　　D．58° 　　　 第 3 题图 第 4 题图　　　　　　　　 4．如图所示，Rt△ABC 向右翻滚，下列说法：(1)①→②是旋转； (2)①→③是平移；(3)①→④是平移；(4)②→③是旋转．其中正确的有 (　C　) A．1 个　　　 B．2 个　　　 C．3 个　　　 D．4 个 5．下列说法中错误的是(　B　) A．成中心对称的两个图形全等 B．成中心对称的两个图形中，对称点的连线被对称轴平分 C．中心对称图形的对称中心是对称点连线的中心 D．中心对称图形绕对称中心旋转 180°后，都能与自身重合 6．如图，在△ABC 中，∠C＝90°，AC＝4，BC＝3，将△ABC 绕点 A 逆时针旋转，使点 C 落在线段 AB 上的点 E 处，点 B 落在点 D 处，则 B，D 两点间的距离为（ C ） A．2 2 B．3 C. 10 D．2 5 7．如图，若将△ABC 绕点 C 顺时针旋转 90°后得到△DEC，则 A 点的 对应点 D 的坐标是（ C ） A．(－3，－2) B．(2，2) C．(3，0) D．(2，1) 8．若点 P(3，－n)，Q(m，－4)关于原点对称，则 P，Q 两点间的距离 为( B ) A．5 B．10 C．20 D．10 2 9．将五个边长都为 2 cm 的正方形按如图所示的样子摆放，点 A，B， C，D 分别是四个正方形的中心，则图中四块阴影部分面积的和为(　B　) A．2 cm2 B．4 cm2 C．6 cm2 D．8 cm2 第 9 题图　　 第 10 题图 10．(2018·桂林)如图，在正方形 ABCD 中，AB＝3，点 M 在 CD 的边 上，且 DM＝1，△AEM 与△ADM 关于 AM 所在的直线对称，将△ADM 按 顺时针方向绕点 A 旋转 90°得到△ABF，连接 EF，则线段 EF 的长为( C ) A．3 B．2 3 C. 13 D. 15 二、填空题(本大题共 8 小题，每小题 3 分，共 24 分) 11．如图所示，等边三角形 ABC 经过顺时针旋转后成为△EBD，则其 旋转中心是点 B，旋转角度是 120°. 第 11 题图　　　 第 12 题图 12．在直角坐标系中，已知点 A(3，4)，由点 A 分别向 x 轴，y 轴作垂 线，垂足为 M，N，当矩形 OMAN 绕点 O 旋转 180°后得到矩形 OM1A1N1(如 图所示)，则 OM1＝OM＝3，ON1＝ON＝4，点 A1 的坐标为(－3，－4)． 13．下列各组图中，图形甲变成图形乙，既能用平移，又能用旋转的 是③. 14．如图，将△ABC 绕点 A 顺时针旋转 60°得到△AED，若线段 AB＝ 3，则 BE＝ 3 . 第 14 题图　　 第 15 题图 15．如图是中国共产主义青年团团旗上的图案(图案本身没有字母)， 则至少旋转 72 度后能与原来图形重合． 16．如图所示，在等边△ABC 中，AC＝9，点 O 是 AC 上的一点，且 OA＝3，点 P 是 AB 上的一动点，连接 OP，将线段 OP 绕点 O 逆时针旋转 60°得到线段 OD，若点 D 恰好落在 BC 上，则 AP 的长度是 6 . 第 16 题图 第 17 题图　 第 18 题图　 17．(2018·随州)如图，在平面直角坐标系 xOy 中，菱形 OABC 的边长 为 2，点 A 在第一象限，点 C 在 x 轴正半轴上，∠AOC＝60°，若将菱形 OABC 绕点 O 顺时针旋转 75°，得到四边形 OA′B′C′，则点 B 的对应点 B′的坐标 为( 6，－ 6)． 18．如图，已知△ABC 中，AB＝AC，∠BAC＝90°，直角∠EPF 的顶 点 P 是 BC 的中点，两边 PE，PF 分别交 AB，AC 于点 E，F，给出以下五 个结论：①AE＝CF；②∠APE＝∠CPF；③△EPF 是等腰直角三角形；④EF＝ AP；⑤S 四边形 AEPF＝1 2 S△ABC.当∠EPF 在△ABC 内绕顶点 P 旋转时(点 E 不 与 A，B 重合)，上述结论中始终正确的有①②③⑤(填序号)． 三、解答题(本大题共 7 小题，共 66 分) 19．(8 分)直角坐标系第二象限内的点 P(x 2＋2x，3)与另一点 Q(x＋2， y)关于原点对称，试求 x＋2y 的值． 解：根据题意得(x2＋2x)＋(x＋2)＝0，y＝－3. ∴x1＝－1，x2＝－2.∵点 P 在第二象限，∴x2＋2x＜ 0. ∴x＝－1.∴x＋2y＝－7. 20.(8 分)如图所示，边长为 a 的正方形 ABCD 绕点 D 旋转 30°后能与四 边形 A′B′C′D 重合． (1)四边形 A′B′C′D 是怎样的图形，面积是多少？ (2)求∠C′DC 和∠CDA′的度数； (3)连接 AA′，求∠DAA′的度数． 解：(1)四边形 A′B′C′D 是正方形， 面积为 a2； (2)∠C′DC＝30 °，∵∠A′DC′＝∠ADC＝90 °， ∴∠CDA′＝∠A′DC′－∠C′DC＝60°； (3)∵AD＝A′D， ∴∠DAA′＝∠DA′A＝1 2 (180°－30°)＝75°， 即∠DAA′＝75°. 21．(8 分)如图，已知点 P 是正方形 ABCD 内的一点，连接 PA，PB， PC.将△PAB 绕点 B 顺时针旋转 90°到△P′CB 的位置． (1)设 AB 的长为 a，PB 的长为 b(b 3 3 时，BC 与⊙O 相离． 21．(8 分)如图，四边形 ABCD 内接于⊙O，点 E 在对角线 AC 上，EC ＝BC＝DC. (1)若∠CBD＝39°，求∠BAD 的度数； (2)求证：∠1＝∠2. (1)解：∵BC＝DC，∴ BC︵ ＝DC︵ ，∴∠BAC＝∠CDB＝∠CBD＝39°， ∴∠BAD＝∠BAC＋∠CAD＝39°＋39°＝78°. (2)证明：∵EC＝BC，∴∠CEB＝∠CBE. ∵∠CEB＝∠2＋∠BAE，∠CBE＝∠1＋∠CBD， ∴∠2＋∠BAE＝∠1＋∠CBD.∵∠BAE＝∠CBD，∴∠1＝∠2. 22．(8 分)如图，四边形 ABCD 是矩形，以 AD 为直径的⊙O 交 BC 边 于点 E，F，AB＝4，AD＝12.求线段 EF 的长． 解：作 OM⊥BC 于 M，连接 OE. ∴ME＝MF＝1 2 EF.∵AD＝12，∴OE＝6. 在矩形 ABCD 中，OM⊥BC，∴OM＝AB＝4.在△OEM 中，∠OME＝ 90 °， ∴ME＝ OE2－OM2＝ 62－42＝2 5.∴EF＝2ME＝4 5. 23.(10 分)如图，在△ABC 中，以 AB 为直径的⊙O 分别与 BC，AC 相 交于 D，E，BD＝CD，过点 D 作⊙O 的切线交边 AC 于点 F. (1)求证：DF⊥AC； (2)若⊙O 的半径为 5，∠CDF＝30°，求BD︵ 的长．(结果保留 π) (1)证明：连接 OD， ∵DF 是⊙O 的切线，D 为切点， ∴OD⊥DF，∴∠ODF＝90°. ∵BD＝CD，OA＝OB， ∴OD 是△ABC 的中位线， ∴OD∥AC，∴∠CFD＝∠ODF＝90°， ∴DF⊥AC. (2)解：∵∠CDF＝30°，由(1)得∠ODF＝90°， ∴∠ODB＝180°－∠CDF－∠ODF＝60°. ∵OB＝OD， ∴△OBD 是等边三角形，∴∠BOD＝60°， ∴lBD︵ ＝nπR 180 ＝60π × 5 180 ＝5 3 π. 24．(12 分)(2018·沈阳)如图，BE 是⊙O 的直径，点 A 和点 D 是⊙O 上的两点，过点 A 作⊙O 的切线交 BE 延长线于点 C. (1)若∠ADE＝25°，求∠C 的度数； (2)若 AB＝AC，CE＝2，求⊙O 的半径的长． 解：(1)连接 OA. ∵AC 为⊙O 的切线，OA 是⊙O 的半径， ∴OA⊥AC，∴∠OAC＝90°. ∵AE︵ ＝AE︵ ，∠ADE＝25°， ∴∠AOE＝2∠ADE＝50°， ∴∠C＝90°－∠AOE＝90°－50°＝40°. (2)∵AB＝AC，∴∠B＝∠C. ∵AE︵ ＝AE︵ ，∴∠AOC＝2∠B，∴∠AOC＝2∠C. ∵∠OAC＝90°，∴∠AOC＋∠C＝90°，∴3∠C＝90°， ∴∠C＝30°.∵∠OAC＝90°，∴OA＝1 2 OC. 设⊙O 的半径为 r，∵CE＝2，∴r＝1 2 (r＋2)，∴r＝2， ∴⊙O 的半径为 2. 25．(12 分)(2018·曲靖)如图，AB 是⊙O 的直径，点 C 是⊙O 上一点， 将BC︵ 沿直线 BC 翻折，使BC︵ 的中点 D 恰好与圆心 O 重合，连接 OC，CD， BD，过点 C 的切线与线段 BA 的延长线交于点 P，连接 AD，在 PB 的另一 侧作∠MPB＝∠ADC， (1)判断 PM 与⊙O 的位置关系，并说明理由； (2)若 PC＝ 3，求四边形 OCDB 的面积． 解：(1)PM 与⊙O 相切．理由：连接 OD，过点 O 作 OE⊥PM 于点 E. ∵点 D 是BC︵ 的中点，∴CD＝BD， 根据翻折的性质可得 CD＝OC＝BD＝OB， ∴四边形 OCDB 是菱形，∴BD∥OC. ∵AB 是⊙O 的直径，∴AD⊥BD，∴OC⊥AD. ∵PC 与⊙O 相切，∴OC⊥PC，∴AD∥PC， ∴四边形 APCD 是平行四边形，∴∠OPC＝∠ADC. ∵∠MPB＝∠ADC，∴∠MPB＝∠OPC，即 PB 平分∠MPC. ∵OE＝OC， ∴PM 与⊙O 相切； (2)由(1)得四边形 OCDB 是菱形． 则 CD＝BD＝OC＝OB＝OD. ∴△OCD 与△OBD 都是等边三角形． ∴∠OCD＝∠OBD＝60°. 又∵CD∥OB，∴∠OCD＝∠POC＝60°， ∵PC 与⊙O 相切，∴OC⊥PC，即∠PCO＝90°， ∴∠OPC＝30°，∴OP＝2OC，∴PC＝ OP2－OC2＝ 3OC， ∴OC＝ 1 3 PC＝1. 过点 C 作 CF⊥AB 于点 F， 则 CF＝1 2 PC＝ 3 2 ， ∴S 四边形 OCDE＝1× 3 2 ＝ 3 2 . 九上数学第二十五章检测题(R)　　　　　　　　　　　　　　　　　　　　　　　 (时间：120 分钟　　满分：150 分) 一、选择题(本大题共 10 小题，每小题 3 分，共 30 分) 1．(本溪中考)下列事件为确定事件的是(　B　) A．一个不透明的口袋中装有除颜色以外完全相同的 3 个红球和 1 个 白球，均匀混合后，从中任意摸出一个球是红球 B．长度分别是 4，6，9 的三条线段能围成一个三角形 C．本钢篮球队运动员韩德军投篮一次命中 D．掷一枚质地均匀的硬币，落地时正面朝上 2．(2018·衡阳)已知抛一枚均匀硬币正面朝上的概率为1 2 ，下列说法错 误的是( A ) A．连续抛一枚均匀硬币 2 次必有 1 次正面朝上 B．连续抛一枚均匀硬币 10 次都可能正面朝上 C．大量反复抛一枚均匀硬币，平均每 100 次有 50 次正面朝上 D．通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的 3．(毕节中考)为了估计鱼塘中鱼的数量，可以先从鱼塘中随机打捞 50 条鱼，在每条鱼身上做上记号后，把这些鱼放归鱼塘，经过一段时间，等 这些鱼完全混合于鱼群后，再从鱼塘中随机打捞 50 条鱼，发现只有 2 条鱼 是前面做了记号的，那么可以估计这个鱼塘鱼的数量约为(　A　) A．1 250 条 B．1 750 条 C．2 500 条 D．5 000 条 4．小红、小明在玩“石头、剪刀、布”游戏，小红给自己一个规定， 一直不出“石头”．小红、小明获胜的概率分别是 P1，P2，则下列结论正 确的是（ B ） A．P1>P2 B．P1＝P2 C．P1