江苏省无锡市2017年中考数学试题 13页

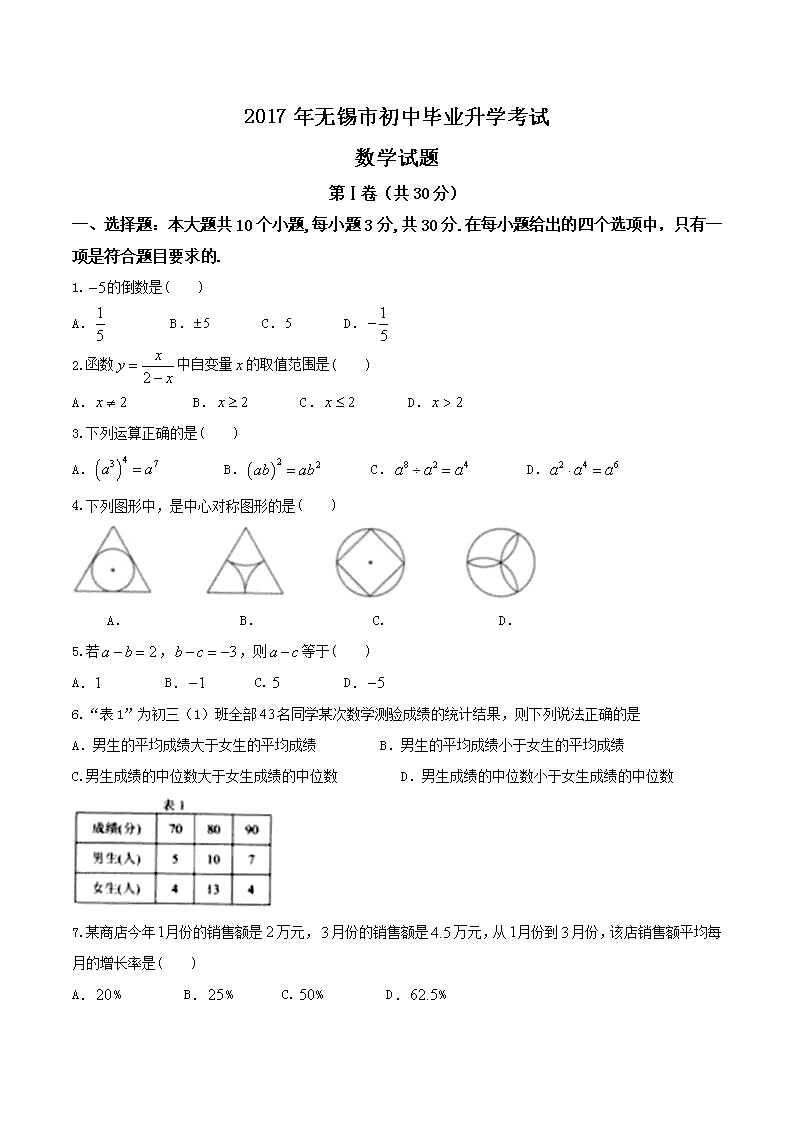
‎2017年无锡市初中毕业升学考试 数学试题 第Ⅰ卷（共30分）‎ 一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.的倒数是( ) ‎ A． B． C． D．‎ ‎2.函数中自变量的取值范围是( )‎ A． B． C． D．‎ ‎3.下列运算正确的是( )‎ A． B． C． D．‎ ‎4.下列图形中，是中心对称图形的是( )‎ A． B． C. D．‎ ‎5.若，，则等于( )‎ A． B． C. 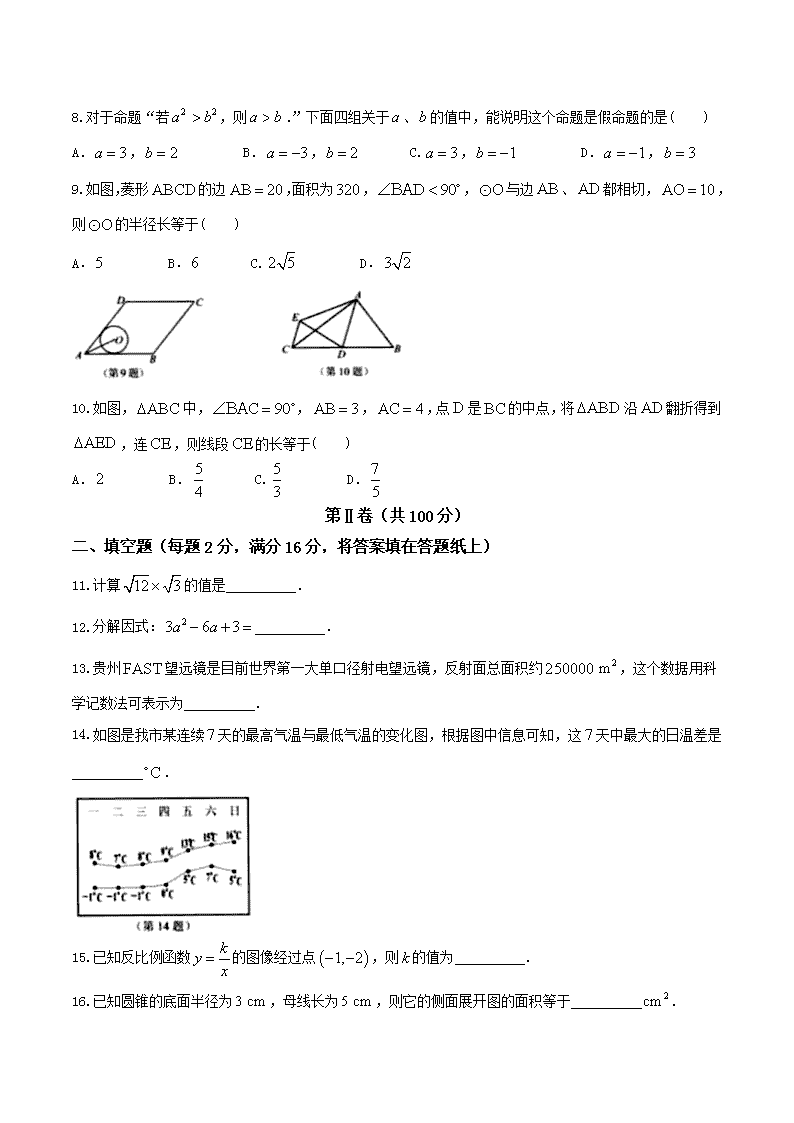D．‎ ‎6.“表‎1”‎为初三（1）班全部名同学某次数学测验成绩的统计结果，则下列说法正确的是 A．男生的平均成绩大于女生的平均成绩 B．男生的平均成绩小于女生的平均成绩 C.男生成绩的中位数大于女生成绩的中位数 D．男生成绩的中位数小于女生成绩的中位数 ‎7.某商店今年月份的销售额是万元，月份的销售额是万元，从月份到月份，该店销售额平均每月的增长率是( )‎ A．% B．% C.% D．%‎ ‎8.对于命题“若，则．”下面四组关于、的值中，能说明这个命题是假命题的是( )‎ A．， B．， C.， D．，‎ ‎9.如图，菱形的边，面积为，，与边、都相切，，则的半径长等于( )‎ A． B． C. D．‎ ‎10.如图，中，，，，点是的中点，将沿翻折得到，连，则线段的长等于( )‎ A． B． C. 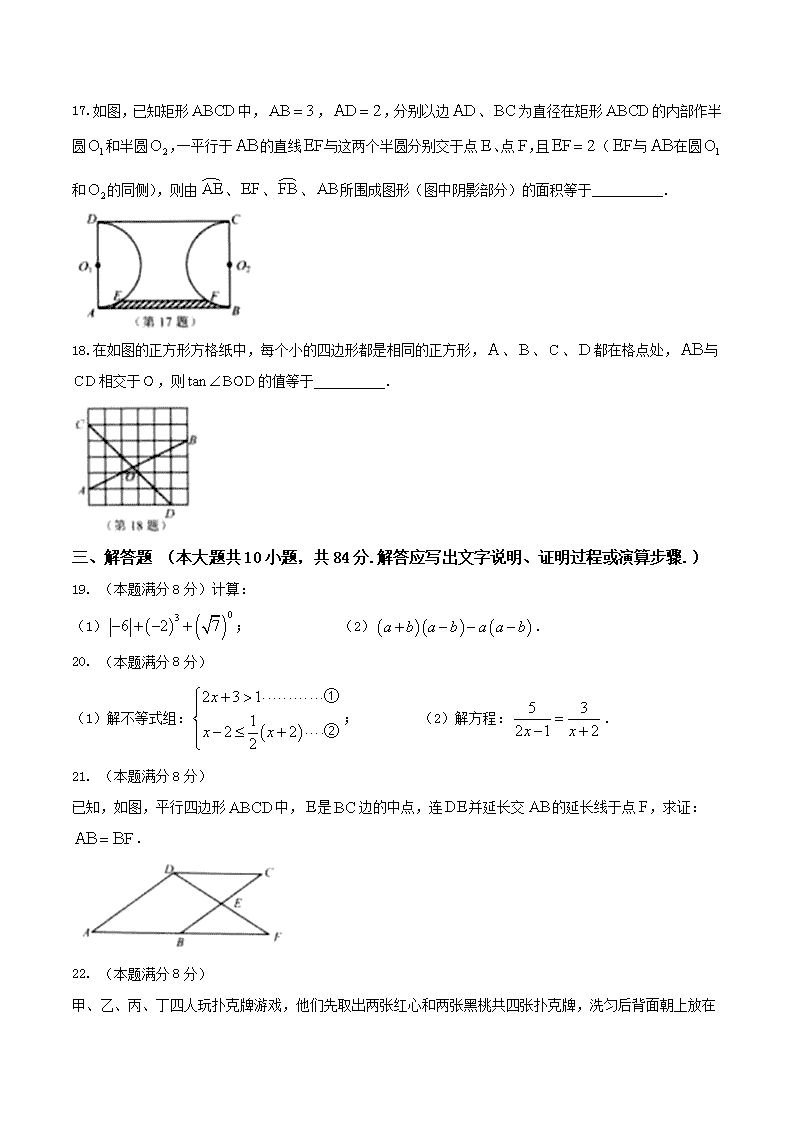D．‎ 第Ⅱ卷（共100分）‎ 二、填空题（每题2分，满分16分，将答案填在答题纸上）‎ ‎11.计算的值是 ．‎ ‎12.分解因式： ．‎ ‎13.贵州望远镜是目前世界第一大单口径射电望远镜，反射面总面积约，这个数据用科学记数法可表示为 ．‎ ‎14.如图是我市某连续天的最高气温与最低气温的变化图，根据图中信息可知，这天中最大的日温差是 ‎ ．‎ ‎15.已知反比例函数的图像经过点，则的值为 ．‎ ‎16.已知圆锥的底面半径为，母线长为，则它的侧面展开图的面积等于 ．‎ ‎17.如图，已知矩形中，，，分别以边、为直径在矩形的内部作半圆和半圆，一平行于的直线与这两个半圆分别交于点、点，且（与在圆和的同侧），则由、、、所围成图形（图中阴影部分）的面积等于 ．‎ ‎18.在如图的正方形方格纸中，每个小的四边形都是相同的正方形，、、、都在格点处，与相交于，则的值等于 ．‎ 三、解答题 （本大题共10小题，共84分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎19. （本题满分8分）计算：‎ ‎（1）； （2）．‎ ‎20. （本题满分8分）‎ ‎（1）解不等式组：； （2）解方程：．‎ ‎21. （本题满分8分）‎ 已知，如图，平行四边形中，是边的中点，连并延长交的延长线于点，求证：．‎ ‎22. （本题满分8分）‎ 甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为游戏搭档．现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请用“画树状图”或“列表”等方法写出分析过程）‎ ‎23. （本题满分8分）‎ 某数学学习网站为吸引更多人注册加入，举行了一个为期天的推广活动．在活动期间，加入该网站的人数变化情况如下表所示：‎ ‎（1）表格中 ， ；‎ ‎（2）请把下面的条形统计图补充完整；‎ ‎（3）根据以上信息，下列说法正确的是 （只要填写正确说法前的序号）．‎ ①在活动之前，该网站已有人加入；‎ ②在活动期间，每天新加入人数逐天递增；‎ ③在活动期间，该网站新加入的总人数为人．‎ ‎24.（本题满分6分）‎ 如图，已知等边，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：‎ ‎（1）作的外心；‎ ‎（2）设是边上一点，在图中作出一个正六边形，使点，点分别在边和上．‎ ‎25.（本题满分10分）‎ 操作：“如图1，是平面直角坐标系中一点（轴上的点除外），过点作轴于点，点绕点逆时针旋转得到点．”我们将此由点得到点的操作称为点的变换．‎ ‎（1）点经过变换后得到的点的坐标为 ；若点经过变换后得到点，则点的坐标为 ．‎ ‎（2）是函数图像上异于原点的任意一点，经过变换后得到点．‎ ①求经过点、点的直线的函数表达式；‎ ②如图2，直线交轴于点，求的面积与的面积之比．‎ ‎26.（本题满分10分）‎ 某地新建的一个企业，每月将产生吨污水．为保护环境，该企业计划购置污水处理器，并在如下两个型号中选择：‎ 已知商家售出的台型、台型污水处理器的总价为万元；售出的台型、台型污水处理器的总价为万元．‎ ‎（1）求每台型、型污水处理器的价格；‎ ‎（2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么他们至少要支付多少钱？‎ ‎27.（本题满分10分）‎ 如图，以原点为圆心、为半径的圆与轴分别交于、两点（点在点的右边），是半径上一点，过且垂直于的直线与分别交于、两点（点在点的上方），直线、交于点．若，‎ ‎（1）求点的坐标；‎ ‎（2）求过点和点，且顶点在直线上的抛物线的函数表达式．‎ ‎28.（本题满分8分）‎ 如图，已知矩形中，，．动点从点出发，在边上以每秒个单位的速度向点运动，连接，作点关于直线的对称点．设点的运动时间为．‎ ‎（1）若，求当、、三点在同一直线上时对应的的值．‎ ‎（2）已知满足：在动点从点到点的整个运动过程中，有且只有一个时刻，使点到直线的距离等于，求所有这样的的取值范围．‎