九年级数学上册第23章图形的相似23-2相似图形第2课时相似图形的性质学案新版华东师大版 3页

第2课时　相似图形的性质 学前温故 若△ABC≌△DEF，则AB＝____，BC＝____，AC＝____，∠A＝____，∠B＝____，∠C＝____.即全等三角形的对应边____，对应角____．‎ 新课早知 ‎1．相似多边形对应边______，对应角____．‎ ‎2．五边形ABCDE的五边长分别为‎50 cm，‎20 cm，‎35 cm，‎38 cm,‎40 cm；另一个和它相似的五边形的最短边长是‎10 cm，则这个五边形的最长边为__________．‎ ‎3．直角梯形的一个角是135°，则与之相似的一个梯形的四个角分别为__________．‎ ‎4．如果两个多边形____________，__________，那么这两个多边形相似．‎ ‎5．下列说法正确的是(　　)．‎ A．两个三角形相似 B．两个矩形相似 C．两个等腰三角形相似 D．两个正方形相似 答案：学前温故 DE　EF　DF　∠D　∠E　∠F　相等　相等 新课早知 ‎1．成比例　相等　‎‎2.25 cm ‎3．90°，90°，135°，45°‎ ‎4．对应边成比例　对应角相等 ‎5．D 相似多边形的性质 ‎【例题】 已知四边形ABCD与四边形A′B′C′D′相似，AB＝‎15 cm，A′B′＝‎10 cm，∠A＝∠A′＝80°，∠B＝∠B′＝90°，∠C＝70°.又BC＝‎20 cm，C′D′＝‎12 cm，AD＝‎16 cm，试求∠C′、∠D、∠D′、B′C′、A′D′的值．‎ 分析：相似多边形的对应角相等，对应边成比例．四边形ABCD与四边形A′B′C′D′相似，其中就暗含着确定的对应关系．‎ 解：由四边形ABCD与四边形A′B′C′D′相似，得∠C＝∠C′＝70°，∠D＝∠D′，‎ 且＝＝＝.‎ 在四边形ABCD中，∠D＝360°－∠A－∠B－∠C＝120°，‎ 所以∠D＝∠D′＝120°.‎ 由AB＝‎15 cm，A′B′＝‎10 cm，BC＝‎20 cm，C′D′＝‎12 cm，AD＝‎16 cm，‎ 得＝＝＝.‎ 解得CD＝‎18 cm，B′C′＝ cm，A′D′＝ cm.‎ 点拨：(1)应用相似多边形的特征求边和角时，关键是找对对应边和对应角，从而列出等式，通过解方程求解．(2)一般地，相等的角是对应角，对应角所夹的边是对应边；对应边所夹的角是对应角；最大(小)的边是对应边；最大(小)的角是对应角．(3)我们在平日的学习中就要养成把对应顶点写在对应的位置上的习惯．‎ 3‎ ‎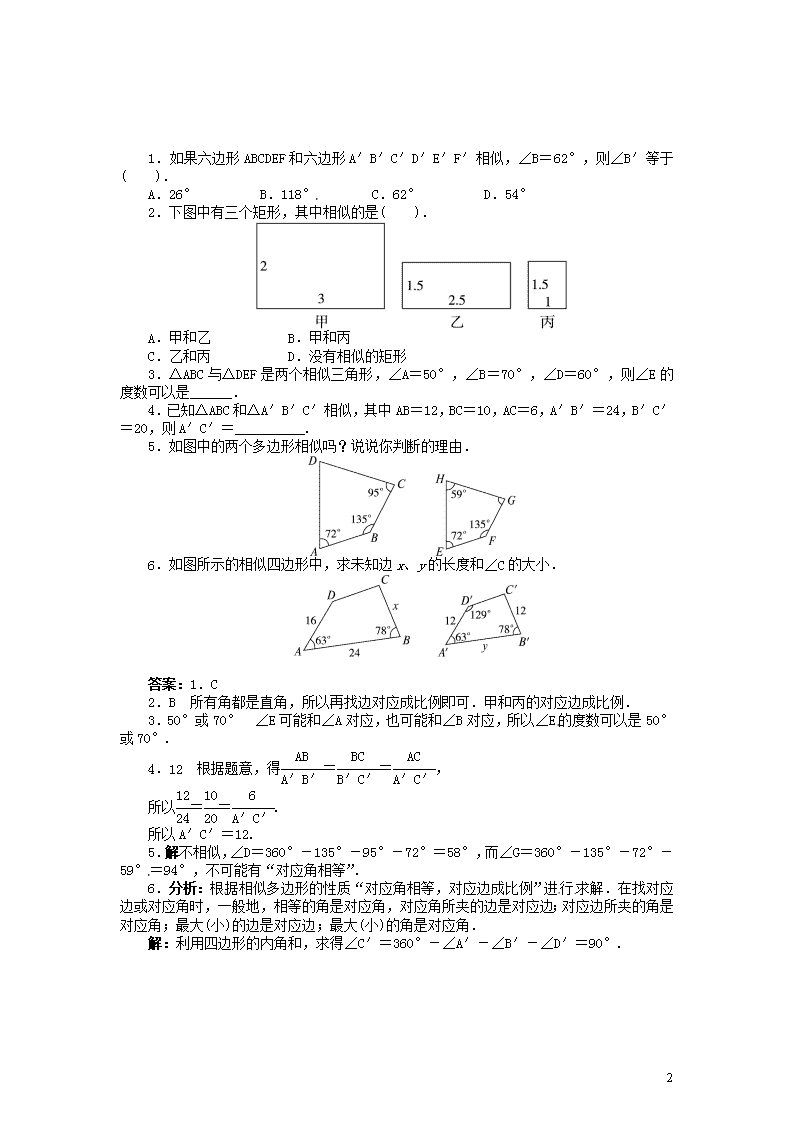1．如果六边形ABCDEF和六边形A′B′C′D′E′F′相似，∠B＝62°，则∠B′等于(　　)．‎ A．26° B．118° C．62° D．54°‎ ‎2．下图中有三个矩形，其中相似的是(　　)．‎ A．甲和乙 B．甲和丙 C．乙和丙 D．没有相似的矩形 ‎3．△ABC与△DEF是两个相似三角形，∠A＝50°，∠B＝70°，∠D＝60°，则∠E的度数可以是______．‎ ‎4．已知△ABC和△A′B′C′相似，其中AB＝12，BC＝10，AC＝6，A′B′＝24，B′C′＝20，则A′C′＝__________.‎ ‎5．如图中的两个多边形相似吗？说说你判断的理由．‎ ‎6．如图所示的相似四边形中，求未知边x、y的长度和∠C的大小．‎ 答案：1．C ‎2．B　所有角都是直角，所以再找边对应成比例即可．甲和丙的对应边成比例．‎ ‎3．50°或70°　∠E可能和∠A对应，也可能和∠B对应，所以∠E的度数可以是50°或70°.‎ ‎4．12　根据题意，得＝＝，‎ 所以＝＝.‎ 所以A′C′＝12.‎ ‎5．解：不相似，∠D＝360°－135°－95°－72°＝58°，而∠G＝360°－135°－72°－59°＝94°，不可能有“对应角相等”．‎ ‎6．分析：根据相似多边形的性质“对应角相等，对应边成比例”进行求解．在找对应边或对应角时，一般地，相等的角是对应角，对应角所夹的边是对应边；对应边所夹的角是对应角；最大(小)的边是对应边；最大(小)的角是对应角．‎ 解：利用四边形的内角和，求得∠C′＝360°－∠A′－∠B′－∠D′＝90°.‎ 根据相似多边形的性质得：∠C＝∠C′＝90°，＝＝，解得x＝16，y＝18.‎ 3‎ 3‎