九年级数学下册第二章二次函数阶段专题复习习题课件北师大版 53页

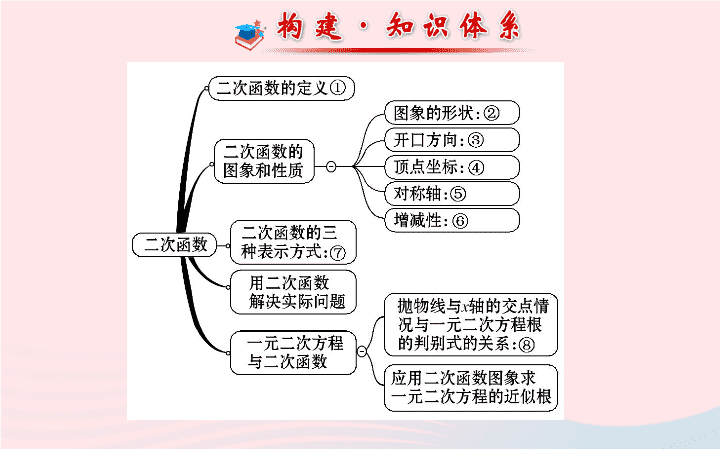
阶段专题复习 第 二 章 请写出框图中数字处的内容 : ①__________________________________________________ _____ ②_______ ③______________________________________________ ④____________ ⑤_________ 形如 y=ax 2 +bx+c(a,b,c 是常数 ,a≠0) 的函数叫做 x 的二次 函数 抛物线 当 a>0 时 , 抛物线开口向上 , 当 a<0 时 , 抛物线开口向下 ⑥___________________________________________________ ____________________________________________________ ___________________________________________ ⑦_______________________ ⑧__________________________________________________ __________ 当 a>0 时 , 在对称轴的左侧 ,y 随 x 的增大而减小 , 在对称轴的 右侧 ,y 随 x 的增大而增大 ; 当 a<0 时 , 在对称轴的左侧 ,y 随 x 的 增大而增大 , 在对称轴的右侧 ,y 随 x 的增大而减小 函数表达式、表格、图象 有两个交点 ⇔ b 2 -4ac>0; 有一个交点 ⇔ b 2 -4ac=0; 没有交点 ⇔ b 2 -4ac<0 考点 1 待定系数法   【 知识点睛 】 　 1. 二次函数表达式常用的三种形式 : (1) 一般式 :y=ax 2 +bx+c(a≠0). (2) 顶点式 :y=a(x-h) 2 +k(a≠0). (3) 交点式 :y=a(x-x 1 )(x-x 2 )(a≠0). 2. 选择不同表达形式求二次函数关系式的技巧 : (1) 当已知抛物线上任意三点时 , 通常设为一般式 y=ax 2 +bx +c(a≠0) 的形式 , 然后组成三元一次方程组来求解 . (2) 当已知抛物线的顶点或对称轴或最大 ( 小 ) 值时 , 通常设为顶点式 y=a(x-h) 2 +k(a≠0) 的形式 . (3) 当已知抛物线与 x 轴的交点 ( 或交点横坐标 ) 或已知抛物线与 x 轴一个交点和对称轴时 , 通常设为交点式 y=a(x-x 1 )(x-x 2 ) (a≠0) 的形式 . 【 例 1】 (2012 · 连云港中考 ) 如图抛物线 y=-x 2 +bx+c 与 x 轴交于 A,B 两点 , 与 y 轴交于点 C, 点 D 为抛物线的顶点 , 点 E 在抛物线上 , 点 F 在 x 轴上 , 四边形 OCEF 为矩形 , 且 OF=2,EF=3. (1) 求该抛物线所对应的函数表达式 . (2) 求△ ABD 的面积 . (3) 将三角形 AOC 绕点 C 逆时针旋转 90°, 点 A 对应点为点 G, 问点 G 是否在该抛物线上 ? 请说明理由 . 【 思路点拨 】 (1) 先表示出 C,E 的坐标 , 然后利用待定系数法确定该函数的表达式 . (2) 根据 (1) 的函数表达式求出 A,B,D 三点的坐标 , 以 AB 为底、 D 点纵坐标的绝对值为高 , 可求出△ ABD 的面积 . (3) 首先根据旋转条件求出 G 点的坐标 , 然后将点 G 的坐标代入抛物线的表达式中进行判断 . 【 自主解答 】 (1) 依题意知， C 点坐标为 (0,3),E 点坐标为 (2 ， 3) ，代入 y= － x 2 +bx+c 中， 得 解得 故抛物线所对应的函数表达式为 y= － x 2 +2x+3. (2)∵y= － x 2 +2x+3= － (x － 1) 2 +4, ∴ 抛物线的顶点坐标为 D(1,4), 又 y=0 时，－ x 2 +2x+3=0, 解得 x 1 =-1,x 2 =3, ∴A 点坐标为 (-1,0),B 点坐标为 (3,0), ∴AB=3-(-1)=4,△ABD 的面积大小为 (3) 当△ AOC 绕点 C 逆时针旋转 90° ， CO 落在 CE 所在的直线上， 又 OA=1, 则点 A 的对应点 G 的坐标为 (3 ， 2), 又当 x=3 时， y= － 3 2 +2×3+3=0≠2, ∴G 点不在该抛物线上 . 【 中考集训 】 1.(2011· 泰安中考 ) 若二次函数 y=ax 2 +bx+c 的 x 与 y 的部分对应 值如下表： 则当 x=1 时， y 的值为 ( ) A.5 B.-3 C.-13 D.-27 x -7 -6 -5 -4 -3 -2 y -27 -13 -3 3 5 3 【 解析 】 选 D. 由表可知，抛物线的顶点为 (-3 ， 5) ，设二次函数的表达式为 y=a(x+3) 2 +5 ， 把 (-2 ， 3) 代入得 a=-2 ， ∴二次函数的表达式为 y=-2(x+3) 2 +5 ， ∴当 x=1 时， y=-27. 2.(2013 · 安徽中考 ) 已知二次函数图象的顶点坐标为 (1,-1), 且过原点 (0,0), 求该函数表达式 . 【 解析 】 ∵ 二次函数图象的顶点坐标为 (1,-1), ∴ 设 y=a(x-1) 2 -1, 当 x=0 时 ,y=0, ∴0=a(0-1) 2 -1,a=1, ∴ 所求函数表达式为 y=(x-1) 2 -1. 3.(2012 · 赤峰中考 ) 如图 , 抛物线 y=x 2 -bx-5 与 x 轴交于 A,B 两点 ( 点 A 在点 B 的左侧 ), 与 y 轴交于点 C, 点 C 与点 F 关于抛物线的对称轴对称 , 直线 AF 交 y 轴于点 E,OC∶OA=5∶1. (1) 求抛物线的表达式 . (2) 求直线 AF 的表达式 . 【 解析 】 (1)∵y=x 2 -bx-5,∴OC=5. ∵OC∶OA=5∶1,∴OA=1. 即 A(-1,0). 把 A(-1,0) 代入 y=x 2 -bx-5 得 (-1) 2 -b×(-1)-5=0, 解得 b=4. ∴ 抛物线的表达式为 y=x 2 -4x-5. (2)∵ 点 C 与点 F 关于对称轴对称， C(0 ， — 5) ， 设 F(x 0 ，－ 5) ， 解得 x 0 =0 或 4 ．∴ F(4 ， -5) ． ∴对称轴为直线 x=2 ． 设直线 AF 的表达式为 y=kx+c ， 把 F(4, － 5) ， A(-1 ， 0) 代入 y=kx+c ， 得 ∴直线 AF 的表达式为 y= － x － 1. 考点 2 二次函数的图象和性质 【 知识点睛 】 1. 系数 a,b,c 与二次函数的图象的关系： (1)a 决定开口方向及开口大小 当 a ＞ 0 时，开口向上，当 a ＜ 0 时，开口向下； |a| 越大，抛物线的开口越小 . (2)b 和 a 共同决定抛物线对称轴的位置 . 由于抛物线 y=ax 2 +bx+c 的对称轴是直线 故： ① b=0 时，对称轴为 y 轴 ; ② ( 即 a,b 同号 ) 时，对称轴在 y 轴左侧 ; ③ ( 即 a,b 异号 ) 时，对称轴在 y 轴右侧 . (3)c 的大小决定抛物线 y=ax 2 +bx+c 与 y 轴交点的位置 . 当 x=0 时 ,y=c,∴ 抛物线 y=ax 2 +bx+c 与 y 轴有且只有一个交点 (0,c). 即 :①c=0, 抛物线经过原点 ;②c>0, 与 y 轴交于正半轴 ; ③c<0, 与 y 轴交于负半轴 . 以上三点中 , 当结论和条件互换时 , 仍成立 . 2. 二次函数图象的平移规律 : 平移不改变图形的形状和大小 , 因此抛物线在平移的过程中 , 图象的形状、开口方向必相同 , 即 a 不变 , 所以抛物线 y=ax 2 +bx+c 可以由 y=ax 2 平移得到 . 其平移的规律用语言来表示可以归结为 : “ 上加下减 , 左加右减 ” , 平移时具体的对应关系可以用下列框图来表示 : 【 例 2】 (2012 · 南昌中考 ) 如图 , 已知二次函数 L 1 :y=x 2 -4x+3 与 x 轴交于 A,B 两点 ( 点 A 在点 B 的左边 ), 与 y 轴交于点 C. (1) 写出二次函数 L 1 的开口方向、对称轴和顶点坐标 . (2) 研究二次函数 L 2 :y=kx 2 -4kx+3k(k≠0). ① 写出二次函数 L 2 与二次函数 L 1 有关图象的两条相同的性质 . ② 若直线 y=8k 与抛物线 L 2 交于 E,F 两点 , 问线段 EF 的长度是否会发生变化 ? 如果不会 , 请求出 EF 的长度 ; 如果会 , 请说明理由 . 【 思路点拨 】 (1) 由 a 的值确定抛物线的开口方向 , 再由对称轴方程和顶点坐标公式确定抛物线的对称轴和顶点坐标 . (2)① 新函数是由原函数的各项系数同时乘以 k 所得 , 因此从二次函数的图象与表达式的系数的关系入手进行分析 . ② 联系直线和抛物线 L 2 的表达式 , 先求出点 E,F 的坐标 , 进而可表示出 EF 的长 , 若该长度为定值 , 则线段 EF 的长不会发生变化 . 【 自主解答 】 (1) 二次函数 L 1 的开口方向向上 , 对称轴是直线 x=2, 顶点坐标是 (2,-1). (2)① 二次函数 L 2 与 L 1 有关图象的两条相同的性质 : 对称轴是直线 x=2 或顶点的横坐标是 2; 都经过 A(1,0),B(3,0) 两点 . ② 线段 EF 的长度不会发生变化 . ∵ 直线 y=8k 与抛物线 L 2 交于 E,F 两点 , ∴kx 2 -4kx+3k=8k, ∵k≠0,∴x 2 -4x+3=8, 解得 x 1 =-1,x 2 =5, ∴EF=x 2 -x 1 =5-(-1)=6, ∴ 线段 EF 的长度不会发生变化 . 【 中考集训 】 　 1.(2012 · 宿迁中考 ) 在平面直角坐标系中 , 若将抛物线 y=2x 2 -4x+3 先向右平移 3 个单位长度 , 再向上平移 2 个单位长度 , 则经过这两次平移后所得抛物线的顶点坐标是　 ( 　　 ) A.(-2,3) B.(-1,4) C.(1,4) D.(4,3) 【 解析 】 选 D.∵y=2x 2 -4x+3=2x 2 -4x+2+1=2(x 2 -2x+1)+1=2(x-1) 2 +1, ∴ 将抛物线 y=2x 2 -4x+3 经两次平移后所得到新抛物线的表达式为 y=2(x-1-3) 2 +1+2, 即 y=2(x-4) 2 +3,∴ 新抛物线的顶点坐标为 (4,3). 2.(2013 · 毕节中考 ) 将二次函数 y=x 2 的图象向右平移 1 个单位长度 , 再向上平移 3 个单位长度所得的图象表达式为 ( 　　 ) A.y=(x-1) 2 +3 B.y=(x+1) 2 +3 C.y=(x-1) 2 -3 D.y=(x+1) 2 -3 【 解析 】 选 A. 将抛物线 y=x 2 的图象向右平移 1 个单位长度所得抛物线表达式为 y=(x-1) 2 , 再向上平移 3 个单位长度所得图象的表达式为 y=(x-1) 2 +3. 3.(2013· 重庆中考 ) 一次函数 y=ax+b(a≠0) ，二次函数 y=ax 2 +bx 和反比例函数 (k≠0) 在同一直角坐标系中 的图象如图所示， A 点的坐标为 (-2 ， 0) ，则下列结论中， 正确的是 ( ) A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0 【 解析 】 选 D. 因为点 A 在一次函数图象上，所以 -2a+b=0, 又 k≠0 ，所以 A 选项错；当 x=-1 时，代入二次函数得 y=a-b ，由 图象可知 y=a-b 为负数，而反比例函数的图象在一、三象限， k>0 ，故选项 B 错误；由上可知， b=2a, 所以选项 C 错误；由图象 知 x=-1 是抛物线的对称轴 . 当 x=-1 时，双曲线的值大于抛物线 的值，即 又 故选项 D 正确 . 4.(2012 · 佳木斯中考 ) 如图 , 抛物线 y=x 2 +bx+c 经过坐标原点 , 并与 x 轴交于点 A(2,0). (1) 求此抛物线的表达式 . (2) 写出顶点坐标及对称轴 . (3) 若抛物线上有一点 B, 且 S △OAB =3, 求点 B 的坐标 . 【 解析 】 (1) 把 (0 ， 0) ， (2 ， 0) 代入 y=x 2 +bx+c 得 所以抛物线的表达式为 y=x 2 － 2x. (2)∵y=x 2 － 2x=(x － 1) 2 － 1 ， ∴顶点坐标为 (1 ，－ 1) ， 对称轴为直线 x=1. (3) 设点 B 的坐标为 (a ， t) ，则 解得 t=3 或 t= － 3 ， ∵顶点纵坐标为－ 1 ，－ 3 ＜－ 1 ( 或方程 x 2 － 2x= － 3 无解 ) ， ∴ t=3 ，∴ x 2 － 2x=3 ，解得 x 1 =3,x 2 = － 1 ， 所以点 B 的坐标为 (3 ， 3) 或 ( － 1 ， 3). 考点 3 二次函数的实际应用 【 知识点睛 】 1. 应用二次函数解决实际问题的基本思路： (1) 理解问题 . (2) 分析问题中的变量和常量以及它们之间的关系 . (3) 用函数表达式表示它们之间的关系 . (4) 计算或求解 , 并应用函数的性质作出判断 . (5) 检验结果的合理性 . 2. 二次函数应用的类型及解题策略： (1) 最值问题 ①利润最大问题的解题策略：先运用“总利润 = 总售价 - 总成本”或“总利润 = 单件商品利润 × 销售数量”建立利润与价格之间的二次函数表达式 , 再求出函数的最值 . ② 几何图形中最值问题的解题策略：先结合面积公式、相似等知识 , 把要讨论的量表示成另一变量的二次函数的形式 , 再求出函数的最值 . (2) 抛物线型问题 解决此类实际问题的关键是进行二次函数建模 , 依据题意 , 建立合适的平面直角坐标系 , 并利用抛物线的性质解决问题 . 【 例 3】 (2012· 茂名中考 ) 每年六七月份我市荔枝大量上市，今年某水果商以 5 元 / 千克的价格购进一批荔枝进行销售，运输过程中质量损耗 5% ，运输费用是 0.7 元 / 千克，假设不计其他费用 . (1) 水果商要把荔枝售价至少定为多少才不会亏本？ (2) 在销售过程中，水果商发现每天荔枝的销售量 m( 千克 ) 与销售单价 x( 元 / 千克 ) 之间满足关系： m= － 10x+120 ，那么当销售单价定为多少时，每天获得的利润 w 最大？ 【 思路点拨 】 (1) 设购进荔枝 k 千克，荔枝售价定为 y 元 / 千克时，水果商才不亏本，由题意建立不等式求出其值即可． (2) 由 (1) 可知，每千克荔枝的平均成本为 6 元，再根据总售价 - 总进价 = 利润就可以表示出利润 w ，然后化为顶点式就可以求出最值． 【 自主解答 】 (1) 设购进荔枝 k 千克，荔枝售价定为 y 元 / 千克时，水果商才不会亏本． 由题意得 y · k(1 － 5%)≥(5+0.7)k ， 由 k>0 可解得 y≥6 ， 所以，水果商要把荔枝售价至少定为 6 元 / 千克才不会亏本 . (2) 由 (1) 可知，每千克荔枝的平均成本为 6 元， 由题意得 w=(x-6)m =(x-6)(-10x+120) =-10(x-9) 2 +90 ， 因此，当 x=9 时， w 有最大值． 所以，当销售单价定为 9 元 / 千克时，每天可获利润 w 最大 . 【 中考集训 】 1.(2012· 扬州中考 ) 如图，线段 AB 的长为 2 ， C 为 AB 上一个动点，分别以 AC,BC 为斜边在 AB 的同侧作两个等腰直角三角形△ ACD 和△ BCE ，那么 DE 长的最小值是 ______. 【 解析 】 设 AC ＝ x, 则 BC ＝ 2-x, ∵△ACD 和△ BCE 都是等腰直角三角形， ∴∠DCE=180° － 45°-45°=90°. 在 Rt△DCE 中， DE 2 =DC 2 +CE 2 ， =(x-1) 2 +1. ∴ 当 x=1 时， DE 2 有最小值，最小值为 1 ，此时 DE 有最小值 1. 答案： 1 2.(2013 · 南充中考 ) 某商场购进一种每件价格为 100 元的新商品 , 在商场试销发现 : 销售单价 x( 元 / 件 ) 与每天销售量 y( 件 ) 之间满足如图所示的关系 : (1) 求出 y 与 x 之间的函数关系式 . (2) 写出每天的利润 W 与销售单价 x 之间的函数关系式 ; 若你是商场负责人 , 会将售价定为多少 , 来保证每天获得的利润最大 , 最大利润是多少 ? 【 解析 】 (1) 设 y 与 x 之间的函数关系式为 y=kx+b(k≠0). 由所给函数图象得 解得 ∴函数关系式为 y=-x+180. (2)W=(x-100)y=(x-100)(-x+180) =-x 2 +280x-18 000 =-(x-140) 2 +1 600. 当 x=140 时， W 最大 =1 600. ∴ 售价定为 140 元 / 件时，每天最大利润 W=1 600 元 . 3.(2012 · 六盘水中考 ) 如图 , 已知△ ABC 中 ,AB=10cm, AC=8cm, BC=6cm. 如果点 P 由 B 出发沿 BA 方向向点 A 匀速运动 , 同时点 Q 由 A 出发向点 C 匀速运动 , 它们的速度均是 2cm/s, 连接 PQ, 设运动的 时间为 t( 单位 :s)(0≤t≤4). 解答下列问题 : (1) 当 t 为何值时 ,PQ∥BC. (2) 设△ AQP 的面积为 S( 单 位 :cm 2 ), 当 t 为何值时 ,S 取 得最大值 , 并求出最大值 . 【 解析 】 (1) 若 QP∥BC ，则△ AQP∽△ACB, 解得， ∴当 时， PQ∥BC. (2)∵8 2 +6 2 =10 2 ， ∴∠ C=90° ， 过 P 作 PH⊥AC 于 H ，则 PH∥BC ， 于是△ APH∽△ABC ， 解得， ∴ ∴当 时， S 取最大值为