北师大版九年级数学下册课件-期末综合测试卷，精品大全 92页

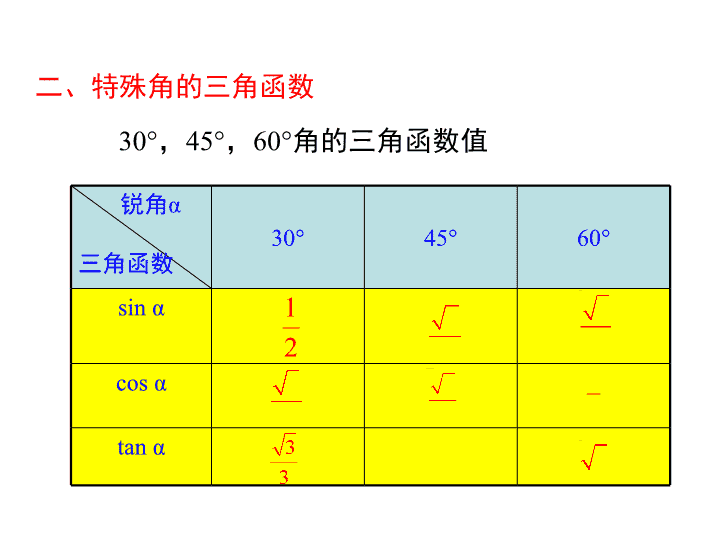
要点梳理 一、锐角三角函数 1.如图所示，在Rt△ABC中，∠C＝90°， a，b，c分别是∠A，∠B，∠C的对边． (2)∠A的余弦：cosA＝　　　　　　　　＝　　　； (3)∠A的正切：tanA＝　　　　　　　　＝　　　　. 2.梯子的倾斜程度与tanA、sinA和cosA的关系： tanA的值越大,梯子越陡; sinA的值越大,梯子越陡; cosA的值越小,梯子越陡. 3.锐角三角函数的增减性： 当角度在0°～90°之间变化时，正弦值和正切值随 着角度的增大（或减小）而 _______ ； 余弦值随着角度的增大（或减小）而 _______ . 增大（或减小） 减小（或增大） 30°，45°，60°角的三角函数值 锐角α 三角函数 30° 45° 60° sin α cos α tan α 1 2 二、特殊角的三角函数 合作探究 1.解直角三角形的依据 (1)在Rt△ABC中，∠C＝90°，a，b，c分别是∠A， ∠B,∠C的对边． 三边关系：　 　； 三角关系：　 ； 边角关系：sinA＝cosB＝　　　，cosA＝sinB＝ ， tanA＝　　　　　　，tanB＝　　　　　　. a2＋b2＝c2 ∠A＝90°－∠B　 三、解直角三角形 = a b = b a (2)直角三角形可解的条件和解法 条件：解直角三角形时知道其中的2个元素(至少有 一个是边)，就可以求出其余的3个未知元素． 解法：①一边一锐角，先由两锐角互余关系求出另 一锐角；知斜边，再用正弦(或余弦)求另两边；知直角 边用正切求另一直角边，再用正弦或勾股定理求斜边； ②知两边：先用勾股定理求另一边，再用边角关系求锐 角；③斜三角形问题可通过添加适当的辅助线转化为解 直角三角形问题． 1.利用计算器求三角函数值． 第二步：输入角度值， 屏幕显示结果. （有的计算器是先输入角度再按函数名称键） 第一步：按计算器 、 、 键，sin tan cos 四、锐角三角函数的计算 2.利用计算器求锐角的度数． 还可以利用 键，进一步得到角 的度数. 第二步：然后输入函数值 屏幕显示答案（按实际需要进行精确） 第一种方法： °＇″2nd F 第一步：按计算器 、 、 键，2nd F sin cos tan 第一步：按计算器 键，°＇″2nd F 第二种方法： 第二步：输入锐角函数值 屏幕显示答案（按实际需要选取精确值）. 1.仰角和俯角 铅 直 线 水平线 视线 视线 仰角 俯角 　　在进行测量时，从下向上看，视线与水平 线的夹角叫做仰角；从上往下看，视线与水平 线的夹角叫做俯角. 五、三角函数的应用 • 以正南或正北方向为准，正南或正北方向线与目标 方向线构成的小于900的角,叫做方向角.如图所示： 30° 45° B O A 东西 北 南 2.方向角 45° 45° 西南 O 东北 东西 北 南 西北 东南 α l h h : l（1）坡角 坡面与水平面的夹角叫做坡角，记作α . （2）坡度（或坡比） 坡度通常写成1∶ m的形式，如1∶ 6. 如图所示，坡面的铅垂高度（h）和水平长度（l） 的比叫做坡面的坡度（或坡比）,即 —h l （3）坡度与坡角的关系 tanh l 坡度等于坡角的正切值 坡 面 水平面 3.坡角 利用解直角三角形的知识解决实际问题的一般过程是： （1）将实际问题抽象为数学问题（画出平面图形，转 化为解直角三角形的问题）； （2）根据条件的特点，适当选用锐角三角函数等去解 直角三角形； （3）得到数学问题的答案； （4）得到实际问题的答案． A C M N (1)在测点A安置测倾器，测得M的仰角∠MCE=α； E (2)量出测点A到物体底部N的水平距离AN=l； (3)量出测倾器的高度AC=a，可求出MN的高度. MN=ME+EN=l·tanα+a α 1. 测量底部可以到达的物体的高度步骤： 六、利用三角函数测高 2.测量东方明珠的高度的步骤是怎么样的呢？ (1)在测点A处安置测倾器，测得此时M的仰角∠MCE=α； A C B D M N Eα (2)在测点A与物体之间的B处安置测倾器，测得此时M的仰角 ∠MDE=β； β (3)量出测倾器的高度AC=BD=a，以及测点A,B之间的距离 AB=b.根据测量数据,可求出物体MN的高度. ,tan tan ME ME b MN ME a     考点一 求三角函数的值 考点讲练 例1 在△ABC中，∠C＝90°，sinA＝ ， 则tanB＝(　　) A.　　 B.　 　 C.　 D. 【解析】 根据sinA＝ ，可设三角形的两边长分 别为4k,5k，则第三边长为3k，所以tanB＝ 4 5 4 3 3 4 3 5 4 5 4 5 3 3 .4 4 k k  B 针对训练 1.如图，在网格中，小正方形的边长均为1，点A，B， C都在格点上，则∠ABC的正弦值是________.5 5 2.用计算器求下列各式的值： （1）cos63°17′≈______； （2）tan27.35°≈______； （3）sin39°57′6″≈______． 0.4 50.52 0.64 3.已知sinα=0.2，cosβ=0.8，则α+β=__________ （精确到1′）． 48°24′ 考点二 特殊角的三角函数值 例2 【解析】本题考查数的0次幂、分母有理化和特殊 角的三角函数值． 解：原式＝ (1) tan30°＋cos45°＋tan60° (2) tan30°· tan60°＋ cos230° 4. 计算： 3 333 4 7 4     3 2 33 2    4 3 2 3 2   针对训练 考点三 解直角三角形 例3.如图，在△ABC中，∠C＝90°，点D在BC上， BD＝4，AD＝BC，cos∠ADC= ， 求：（1）DC的长；（2）sinB的值． 5 3 【分析】题中给出了两个直角三角 形，DC和sinB可分别在Rt△ACD和 ABC中求得，由AD＝BC，图中CD ＝BC－BD，由此可列方程求出 CD． A B CD 解:(1)设CD＝x，在Rt△ACD中，cos∠ADC= , 又 BC－CD＝BD， 解得x=6， ∴CD=6. A B CD 3 5 3 5, .5 3 x AD xAD     5, ,3AD BC BC x   5 43 x x   ， (2) BC=BD+CD=4+6=10=AD 在Rt△ACD中 在Rt△ABC中 2 2 2 210 6 8,AC AD CD     2 2 64 100 2 41AB AC BC     8 4 41sin 412 41 ACB AB     A B CD 5.如图所示，在Rt△ABC中，∠C＝90°，AC＝ . 点D为BC边上一点，且BD＝2AD，∠ADC＝60°. 求△ABC的周长(结果保留根号). 针对训练 3 解：在Rt△ADC中， ∴BD＝2AD＝4. ∴BC＝BD＋DC＝5. 在Rt△ABC中， ∴△ABC的周长＝AB＋BC＋AC 考点四 三角函数的应用 例4 如图，在一次数学课外实践活动中，要求测 教学楼AB的高度．小刚在D处用高1.5 m的测角仪 CD，测得教学楼顶端A的仰角为30°，然后向教学 楼前进40 m到达EF，又测得教学楼顶端A的仰角为 60°.求这幢教学楼AB的高度． 【分析】 设CF与AB交于点G，在 Rt△AFG中，用AG表示出FG，在 Rt△ACG中，用AG表示出CG，然 后根据CG－FG＝40，可求AG. 解：设CF与AB交于点G，在Rt△AFG中， tan∠AFG＝ ，∴FG＝ 在Rt△ACG中，tan∠ACG＝ ， 又CG－FG＝40， ∴AG＝ ，∴AB＝ 答：这幢教学楼AB的高度为 20 3 (20 3 1.5)(m). (20 3 1.5)m. ∴ 6.如图某人站在楼顶观测对面的笔直的旗杆AB，已知 观测点C到旗杆的距离（即CE的长）为8米，测得旗杆 顶的仰角∠ECA为30°，旗杆底部的俯角∠ECB为45 °，则旗杆AB的高度是多少米? C A B D E 解：如图在Rt△ACE和Rt△BCE中 ∠ACE=30°，EC=8米 ∴tan∠ACE= ,tan∠ECB= 即：AE=8tan30°= （米） EB=8tan45°=8（米） ∴AE+EB=(8+ )米 AE EC EB EC 8 3 3 8 3 3 针对训练 锐角三角 函数 特殊角的三 角函数 解直角三 角形 简单实际 问题 c a b A BC 课堂小结 见《学练优》本章热点专练 课后作业 1.当a为何值时,不等式组 x - 2 ≤ ≤ +1 的解集中只有一个解?并求这个解 3 a 4 32 x 2 1 x a=-18，x=-4 §2、已知关于x的不等式2x-a≤-1的解集是x≤-1，则a的 取值是__________. 3、若不等式组 的解集是-1b.1 – 5a ––– 1 -5b （ 3 ）、当 2a≤3b时，a－b –––　 b2 1 期末综合测试卷 B A A A A B B C A B