2019福建各地市九年级上期末数学质检卷及答案 55页

书书书 ２０１８～２０１９学年度福州市九年级第一学期质量调研 数学试卷 一、选择题（本题共 １０小题，每小题 ４分，共 ４０分．在 每小题给出的四个选项中，只有一项是符合题目 要求的） １．下列图形是中心对称图形的是 （　　） ２．气象台预报“本市明天降水概率是 ８３％”．对此信 息，下列说法正确的是 （　　） Ａ．本市明天将有 ８３％的时间降水 Ｂ．本市明天将有 ８３％的地区降水 Ｃ．本市明天肯定下雨 Ｄ．本市明天降水的可能性比较大 ３．在平面直角坐标系中，点（２，６）关于原点对称的点 的坐标是 （　　） Ａ．（－２，－６）　　　　　　Ｂ．（－２，６） Ｃ．（－６，２） Ｄ．（６，２） ４．如图，测得 ＢＤ＝１２０ｍ，ＤＣ＝６０ｍ，ＥＣ＝５０ｍ，则小 河宽 ＡＢ的长是 （　　） 第 ４题图 Ａ．１８０ｍ Ｂ．１５０ｍ Ｃ．１４４ｍ Ｄ．１００ｍ ５．若两个正方形的边长比是 ３∶２，其中较大的正方形 的面积是 １８，则较小的正方形的面积是 （　　） Ａ．４　　　Ｂ．８　　　Ｃ．１２　　　Ｄ．１６ ６．如图，⊙Ｏ的半径 ＯＣ垂直于弦 ＡＢ，Ｄ是优弧 ＡＢ 上的一点（不与点 Ａ，Ｂ重合），若∠ＢＯＣ＝５０°，则 ∠ＡＤＣ等于 （　　） Ａ．４０° Ｂ．３０° Ｃ．２５° Ｄ．２０° 第 ６题图 ７．下列抛物线平移后可得到抛物线 ｙ＝－（ｘ－１）２ 的 是 （　　） Ａ．ｙ＝－ｘ２ Ｂ．ｙ＝ｘ２ －１ Ｃ．ｙ＝（ｘ－１）２ ＋１ Ｄ．ｙ＝（１－ｘ）２ ８．已知关于 ｘ的方程 ｘ２ ＋ａｘ＋ｂ＝０有一个非零根 ｂ， 则 ａ＋ｂ的值是 （　　） Ａ．－２ Ｂ．－１ Ｃ．０ Ｄ．１ ９．如图，矩形 ＡＢＣＤ的对角线 ＢＤ过原点 Ｏ，各边分别 平行于坐标轴，点 Ｃ在反比例函数 ｙ＝３ｋ＋１ ｘ 的图 象上．若点 Ａ的坐标是（－２，－２），则 ｋ的值是 （　　） Ａ．－１ Ｂ．０ Ｃ．１ Ｄ．４ 第 ９题图 １０．已知二次函数 ｙ＝ａｘ２ －２ａｘ＋ｃ，当 －３＜ｘ＜－２ 时，ｙ＞０；当 ３＜ｘ＜４时，ｙ＜０．则 ａ与 ｃ满足的关 系式是 （　　） Ａ．ｃ＝－１５ａ Ｂ．ｃ＝－８ａ Ｃ．ｃ＝－３ａ Ｄ．ｃ＝ａ 二、填空题（本题共 ６小题，每小题 ４分，共 ２４分） １１．如图，在平行四边形纸片上作随机扎针试验，针 头扎在阴影区域内的概率是　　　　． 第 １１题图 １２．二次函数 ｙ＝－（ｘ－２）２ －３的最大值是　　　． １３．在半径为 ４的圆中，１２０°的圆心角所对的弧长是 　　　　． １４．已知 ｘ２ ＋３ｘ－５＝０，则 ｘ（ｘ＋１）（ｘ＋２）（ｘ＋３）的 值是　　　　． １５．我国古代数学著作《增删算法统宗》记载“圆中方 形”问题：“今有圆田一段，中间有个方池．丈量田 地待耕犁，恰好三分在记．池面至周有数，每边三 步无疑．内方圆径若能知，堪作算中第一．”其大 意为：有一块圆形的田，中间有一块正方形水池． 测量出除水池外圆内可耕地的面积恰好 ７２                                                                平方 １ 步，从水池边到圆周，每边相距 ３步远．如果你能 求出正方形边长和圆的直径，那么你的计算水平 就是第一了．设正方形的边长是 ｘ步，则列出的 方程是　　　　． 第 １５题图 １６．如图，等边三角形 ＡＢＣ中，Ｄ是边 ＢＣ上一点，过 点 Ｃ作 ＡＤ的垂线段，垂足为点 Ｅ，连接 ＢＥ，若 ＡＢ ＝２，则 ＢＥ的最小值是　　　　． 第 １６题图 三、解答题（本题共 ９小题，共 ８６分，解答应写出文字 说明、证明过程或演算步骤） １７．（本小题满分 ８分） 解方程：ｘ２ ＋４ｘ＋２＝０． １８．（本小题满分 ８分） 已知函数 ｙ＝ｍｘ２ ＋（２ｍ＋１）ｘ＋ｍ（ｍ为常数）的 图象与 ｘ轴只有一个公共点，求 ｍ的值． １９．（本小题满分 ８分） 小明和小武两人玩猜想数字游戏．先由小武在心 中任意想一个数记为 ｘ，再由小明猜小武刚才想 的数字．把小明猜的数字记为 ｙ，且他们想和猜的 数字只能在 １，２，３，４这四个数字中． （１）用列表法或画树状图法表示出他们想和猜的 所有情况； （２）如果他们想和猜的数字相同，则称他们“心灵 相通”，求他们“心灵相通”的概率． ２０．（本小题满分 ８分） 如图，直线 ＡＢ经过⊙Ｏ上的点 Ｃ，并且 ＯＡ＝ＯＢ， ＣＡ＝ＣＢ．求证：直线 ＡＢ是⊙Ｏ的切线． 　第 ２０题图                                                                       ２ 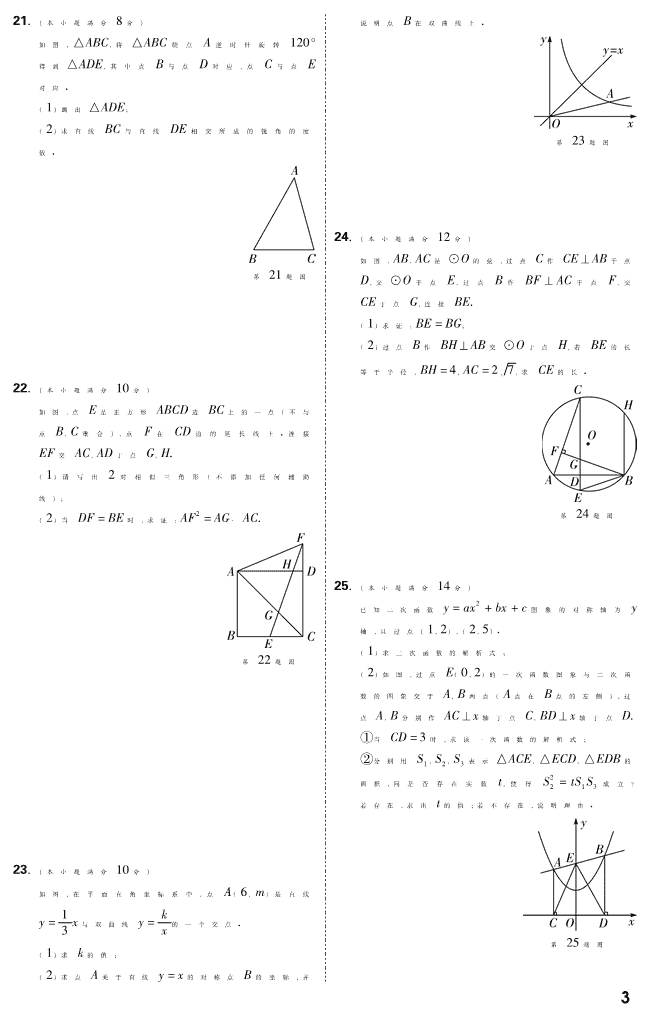２１．（本小题满分 ８分） 如图，△ＡＢＣ，将△ＡＢＣ绕点 Ａ逆时针旋转 １２０° 得到△ＡＤＥ，其中点 Ｂ与点 Ｄ对应，点 Ｃ与点 Ｅ 对应． （１）画出△ＡＤＥ； （２）求直线 ＢＣ与直线 ＤＥ相交所成的锐角的度 数． 　第 ２１题图 ２２．（本小题满分 １０分） 如图，点 Ｅ是正方形 ＡＢＣＤ边 ＢＣ上的一点（不与 点 Ｂ，Ｃ重合），点 Ｆ在 ＣＤ边的延长线上．连接 ＥＦ交 ＡＣ，ＡＤ于点 Ｇ，Ｈ． （１）请写出 ２对相似三角形（不添加任何辅助 线）； （２）当 ＤＦ＝ＢＥ时，求证：ＡＦ２ ＝ＡＧ·ＡＣ． 　第 ２２题图 ２３．（本小题满分 １０分） 如图，在平面直角坐标系中，点 Ａ（６，ｍ）是直线 ｙ＝１ ３ｘ与双曲线 ｙ＝ｋ ｘ的一个交点． （１）求 ｋ的值； （２）求点 Ａ关于直线 ｙ＝ｘ的对称点 Ｂ的坐标，并 说明点 Ｂ在双曲线上． 　第 ２３题图 ２４．（本小题满分 １２分） 如图，ＡＢ，ＡＣ是⊙Ｏ的弦，过点 Ｃ作 ＣＥ⊥ＡＢ于点 Ｄ，交⊙Ｏ于点 Ｅ，过点 Ｂ作 ＢＦ⊥ＡＣ于点 Ｆ，交 ＣＥ于点 Ｇ，连接 ＢＥ． （１）求证：ＢＥ＝ＢＧ； （２）过点 Ｂ作 ＢＨ⊥ＡＢ交⊙Ｏ于点 Ｈ，若 ＢＥ的长 等于半径，ＢＨ＝４，ＡＣ 槡＝２ ７，求 ＣＥ的长． 　第 ２４题图 ２５．（本小题满分 １４分） 已知二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ图象的对称轴为 ｙ 轴，且过点（１，２），（２，５）． （１）求二次函数的解析式； （２）如图，过点 Ｅ（０，２）的一次函数图象与二次函 数的图象交于 Ａ，Ｂ两点（Ａ点在 Ｂ点的左侧），过 点 Ａ，Ｂ分别作 ＡＣ⊥ｘ轴于点 Ｃ，ＢＤ⊥ｘ轴于点 Ｄ． ①当 ＣＤ＝３时，求该一次函数的解析式； ②分别用 Ｓ１，Ｓ２，Ｓ３ 表示△ＡＣＥ，△ＥＣＤ，△ＥＤＢ的 面积，问是否存在实数 ｔ，使得 Ｓ２ ２ ＝ｔＳ１Ｓ３ 成立？ 若存在，求出 ｔ的值；若不存在，说明理由． 　第 ２５题图                                                                       ３ ２０１８－２０１９学年（上）厦门市九年级质量检测 数　学 （试卷满分 １５０分；考试时间 １２０分钟） 一、选择题（本大题有 １０小题，每小题 ４分，共 ４０分． 每小题都有四个选项，其中有且只有一个选项正确） １．计算 －５＋６，结果正确的是 （　　） Ａ．１　　　Ｂ．－１　　　Ｃ．１１　　　Ｄ．－１１ 第 ２题图 ２．如图，在△ＡＢＣ中，∠Ｃ＝９０°，则下列 结论正确的是 （　　） Ａ．ＡＢ＝ＡＣ＋ＢＣ Ｂ．ＡＢ＝ＡＣ·ＢＣ Ｃ．ＡＢ２ ＝ＡＣ２ ＋ＢＣ２ Ｄ．ＡＣ２ ＝ＡＢ２ ＋ＢＣ２ ３．抛物线 ｙ＝２（ｘ－１）２ －６的对称轴是 （　　） Ａ．ｘ＝－６ Ｂ．ｘ＝－１ Ｃ．ｘ＝１ ２ Ｄ．ｘ＝１ ４．要使分式 １ ｘ－１有意义，ｘ的取值范围是 （　　） Ａ．ｘ≠０ Ｂ．ｘ≠１ Ｃ．ｘ＞－１ Ｄ．ｘ＞１ ５．下列事件是随机事件的是 （　　） Ａ．画一个三角形，其内角和是 ３６０° Ｂ．投掷一枚正六面体骰子，朝上一面的点数小于 ７ Ｃ．射击运动员射击一次，命中靶心 Ｄ．在只装了红球的不透明袋子里，摸出黑球 ６．图①，图②分别是某厂六台机床十月份第一天和第 二天生产零件数的统计图．与第一天相比，第二天 六台机床生产零件数的平均数与方差的变化情况 是 （　　） 图① 　　 图② 第 ６题图 Ａ．平均数变大，方差不变 Ｂ．平均数变小，方差不变 Ｃ．平均数不变，方差变小 Ｄ．平均数不变，方差变大 ７．地面上一个小球被推开后笔直滑行，滑行的距离 ｓ 与时间 ｔ的函数关系如图中的部分抛物线所示（其 中 Ｐ是该抛物线的顶点），则下列说法正确的是 （　　） 第 ７题图 Ａ．小球滑行 ６秒停止 Ｂ．小球滑行 １２秒停止 Ｃ．小球滑行 ６秒回到起点 Ｄ．小 球 滑 行 １２秒 回 到 起点 ８．在平面直角坐标系 ｘＯｙ中，已 知 Ａ（２，０），Ｂ（１，－１），将线段 ＯＡ绕点 Ｏ逆时针旋转， 旋转角为 α（０°＜α＜１３５°）．记点 Ａ的对应点为 Ａ１，若 点 Ａ１与点 Ｂ的距离为槡６，则 α为 （　　） Ａ．３０° Ｂ．４５° Ｃ．６０° Ｄ．９０° ９．点 Ｃ，Ｄ在线段 ＡＢ上，若点 Ｃ是线段 ＡＤ的中点， ２ＢＤ＞ＡＤ，则下列结论正确的是 （　　） Ａ．ＣＤ＜ＡＤ－ＢＤ Ｂ．ＡＢ＞２ＢＤ Ｃ．ＢＤ＞ＡＤ Ｄ．ＢＣ＞ＡＤ １０．已知二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ（ａ＞０）的图象经过 （０，１），（４，０）．当该二次函数的自变量分别取 ｘ１， ｘ２（０＜ｘ１ ＜ｘ２ ＜４）时，对应的函数值是 ｙ１，ｙ２，且 ｙ１ ＝ｙ２．设该函数图象的对称轴是 ｘ＝ｍ，则 ｍ的取 值范围是 （　　） Ａ．０＜ｍ＜１ Ｂ．１＜ｍ≤２ Ｃ．２＜ｍ＜４ Ｄ．０＜ｍ＜４ 二、填空题（本大题有 ６小题，每小题 ４分，共 ２４分） １１．投掷一枚质地均匀的正六面体骰子，投掷一次，朝 上一面的点数为奇数的概率是　　　　． １２．已知 ｘ＝２是方程 ｘ２ ＋ａｘ－２＝０的根，则 ａ＝ 　　　　． 第 １３题图 １３．如图，已知 ＡＢ是 ⊙Ｏ的 直 径，ＡＢ＝２，Ｃ，Ｄ是圆周上的 点，且∠ＣＤＢ＝３０°，则 ＢＣ的 长为　　　　． １４．我们把三边长的比为 ３∶４∶５ 的三角形称为完全三角形． 记命题 Ａ：“完全三角形是直角三角形”．若命题 Ｂ 是命题 Ａ的逆命题，请写出命题 Ｂ：　　　　　　 　　　　；并写出一个例子（该例子能判断命题 Ｂ 是错误的）： 　． １５．已知 ＡＢ是⊙Ｏ的弦，Ｐ为 ＡＢ的中点，连接 ＯＡ， ＯＰ，将△ＯＰＡ绕点 Ｏ旋转到△ＯＱＢ．设⊙Ｏ                                                                的半 ４ 径为 １，∠ＡＯＱ＝１３５°，则 ＡＱ的长为　　　　． １６．若抛物线 ｙ＝ｘ２ ＋ｂｘ（ｂ＞２）上存在关于直线 ｙ＝ｘ 成轴对称的两个点，则 ｂ的取值范围是　　　　． 三、解答题（本大题有 ９小题，共 ８６分） １７．（本题满分 ８分） 解方程 ｘ２ －３ｘ＋１＝０． １８．（本题满分 ８分） 化简并求值：（１－ ２ ｘ＋１）÷ｘ２ －１ ２ｘ＋２，其中 ｘ 槡＝ ２－１． １９．（本题满分 ８分） 已知二次函数 ｙ＝（ｘ－１）２ ＋ｎ，当 ｘ＝２时 ｙ＝２， 求该二次函数的解析式，并在平面直角坐标系中 画出该函数的图象． ２０．（本题满分 ８分） 如图，已知四边形 ＡＢＣＤ是矩形． （１）请用直尺和圆规在边 ＡＤ上作点 Ｅ，使得 ＥＢ＝ ＥＣ；（保留作图痕迹） （２）在 （１）的 条 件 下，若 ＡＢ＝４，ＡＤ＝６，求 ＥＢ 的长． 第 ２０题图 ２１．（本题满分 ８分） 如图，在△ＡＢＣ中，∠Ｃ＝６０°，ＡＢ＝４，以 ＡＢ为直 径画⊙Ｏ，交边 ＡＣ于点 Ｄ， ) ＡＤ的长为４π ３．求证：ＢＣ 是⊙Ｏ的切线． 第 ２１题图                                                                       ５ ２２．（本题满分 １０分） 已知动点 Ｐ在边长为 １的正方形 ＡＢＣＤ的内部， 点 Ｐ到边 ＡＤ，ＡＢ的距离分别为 ｍ，ｎ． （１）以 Ａ为原点，以边 ＡＢ所在直线为 ｘ轴，建立 平面直角坐标系，如图①所示．当点 Ｐ在对角线 ＡＣ上，且 ｍ＝１ ４时，求点 Ｐ的坐标； （２）如 图 ②，当 ｍ，ｎ满 足 什 么 条 件 时，点 Ｐ在 △ＤＡＢ的内部？请说明理由． 第 ２２题图 ２３．（本题满分 １０分） 小李的活鱼批发店以 ４４元 ／公斤的价格从港口买 进一批 ２０００公斤的某品种活鱼，在运输过程中， 有部分鱼未能存活．小李对运到的鱼进行随机抽 查，结果如表一．由于市场调节，该品种活鱼的售 价与日销售量之间有一定的变化规律，表二是近 一段时间该批发店的销售记录． （１）请估计运到的 ２０００公斤鱼中活鱼的总重量； （直接写出答案） （２）按此市场调节的规律， ①若该品种活鱼的售价定为 ５２．５元／公斤，请估 计日销售量，并说明理由； ②考虑到该批发店的储存条件，小李打算 ８天内 卖完这批鱼（只卖活鱼），且售价保持不变，求该 批发店每日卖鱼可能达到的最大利润，并说明 理由． 表一 所抽查的 鱼的总重 量 ｍ（公斤） １００ １５０ ２００ ２５０ ３５０ ４５０ ５００ 存活的鱼 的重量与 ｍ的比值 ０．８８５０．８７６０．８７４０．８７８０．８８１０．８８００．８８０ 表二 该品种活鱼的 售价（元／公斤） ５０ ５１ ５２ ５３ ５４ 该品种活鱼的 日销售量（公斤）                                                                       ４００ ３６０ ３２０ ２８０ ２４０ ６ ２４．（本题满分 １２分） 已知 Ｐ是⊙Ｏ上一点，过点 Ｐ作不过圆心的弦 ＰＱ，在劣弧 ＰＱ和优弧 ＰＱ上分别有动点 Ａ，Ｂ（不 与 Ｐ，Ｑ重合），连接 ＡＰ，ＢＰ．若∠ＡＰＱ＝∠ＢＰＱ． （１）如图①，当∠ＡＰＱ＝４５°，ＡＰ＝１，ＢＰ 槡＝２ ２时， 求⊙Ｏ的半径； （２）如图②，连接 ＡＢ，交 ＰＱ于点 Ｍ，点 Ｎ在线段 ＰＭ上（不与 Ｐ，Ｍ重合），连接 ＯＮ，ＯＰ．若∠ＮＯＰ ＋２∠ＯＰＮ＝９０°，探究直线 ＡＢ与 ＯＮ的位置关 系，并证明． 第 ２４题图 ２５．（本题满分 １４分） 在平面直角坐标系 ｘＯｙ中，点 Ａ（０，２），Ｂ（ｐ，ｑ）在 直线 ｌ上，抛物线 ｍ经过点 Ｂ，Ｃ（ｐ＋４，ｑ），且它的 顶点 Ｎ在直线 ｌ上． （１）若 Ｂ（－２，１）， ①请在如图的平面直角坐标系中画出直线 ｌ与抛 物线 ｍ的示意图； ②设抛物线 ｍ上的点 Ｑ的横坐标为 ｅ（－２≤ｅ≤ ０），过点 Ｑ作 ｘ轴的垂线，与直线 ｌ交于点 Ｈ．若 ＱＨ＝ｄ，当 ｄ随 ｅ的增大而增大时，求 ｅ的取值 范围； （２）抛物线 ｍ与 ｙ轴交于点 Ｆ，当抛物线 ｍ与 ｘ轴 有唯一交点时，判断△ＮＯＦ的形状并说明理由． 第 ２５题图                                                                       ７ 泉州市 ２０１８～２０１９学年度上学期初三教学质量检测 数学试题 （满分：１５０分　考试时间：１２０分钟） 学校　　　　　姓名　　　　　座位号　　　　 　　　　　　　　　　 （第Ⅰ卷　选择题　共 ４０分） 一、选择题：本题共 １０小题，每小题 ４分，共 ４０分．在 每小题给出的四个选项中，只有一项符合题目要求， 在答题卡的相应位置内作答． １．下列各数中，能使 ｘ槡 －５有意义的是 （　　） Ａ．０ Ｂ．２ Ｃ．４ Ｄ．６ ２．下列二次根式中与槡２是同类二次根式的是 （　　） Ａ．槡８ Ｂ． ０．槡 ２ Ｃ．槡１２ Ｄ．槡２ ３ ３．若 ａ ｂ＝５ ３，则ａ－ｂ ａ 的值为 （　　） Ａ．２ ３ Ｂ．２ ５ Ｃ．３ ５ Ｄ．－２ ３ ４．用配方法解方程 ｘ２ －６ｘ＋１＝０，下列配方正确的是 （　　） Ａ．（ｘ＋３）２ ＝８ Ｂ．（ｘ－３）２ ＝８ Ｃ．（ｘ＋３）２ ＝９ Ｄ．（ｘ－３）２ ＝９ ５．下列事件为不可能事件的是 （　　） Ａ．掷一枚质地均匀的正方体骰子，掷得的点数不 是奇数就是偶数 Ｂ．从一副扑克牌中任意抽出一张牌，花色是黑桃 Ｃ．抛一枚普通的硬币，正面朝上 Ｄ．从装满红球的袋子中摸出一个白球 ６．若三角形的各边长分别是 ８ｃｍ、１０ｃｍ和 １６ｃｍ，则 以各边中点为顶点的三角形的周长为 （　　） Ａ．３４ｃｍ Ｂ．３０ｃｍ Ｃ．２９ｃｍ Ｄ．１７ｃｍ ７．从一个由 ４个男生、３个女生组成的学习小组中， 随机选出 １人担任小组长，则选出“男生”为小组 长的概率是 （　　） Ａ．１ ４ Ｂ．１ ２ Ｃ．３ ７ Ｄ．４ ７ ８．某斜坡的坡度 ｉ＝１∶槡３ ３，则该斜坡的坡角为 （　　） Ａ．７５° Ｂ．６０° Ｃ．４５° Ｄ．３０° 第 ９题图 ９．如图，在△ＡＢＣ中，点 Ｇ为 △ＡＢＣ的 重 心，过 点 Ｇ作 ＤＥ∥ＢＣ，分别交 ＡＢ，ＡＣ于 点 Ｄ、Ｅ，则△ＡＤＥ与四边形 ＤＢＣＥ的面积之比为（　　） Ａ．２ ３ Ｂ．３ ４ Ｃ．４ ５ Ｄ．４ ９ １０．若关于 ｘ的一元二次方程 ａｘ２ ＋ｂｘ＋ｃ＝０（ａｃ≠０） 有一根为 ｘ＝２０１９，则关于 ｙ的一元二次方程 ｃｙ２ ＋ｂｙ＋ａ＝０（ａｃ≠０）必有一根为 （　　） Ａ． １ ２０１９ Ｂ．－ １ ２０１９ Ｃ．２０１９ Ｄ．－２０１９ （第Ⅱ卷　非选择题　共 １１０分） 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分．把 答案填在答题卡的相应位置． １１．计算：（ 槡３ ２）２ ＝　　　　． １２．方程 ｘ２ －３ｘ＝０的解是　　　　． 第 １４题图 １３．在 Ｒｔ△ＡＢＣ中，∠Ｃ＝９０°，ＢＣ ＝３，ＡＣ＝４，则 ｓｉｎＡ＝　　　． １４．如图，直线 ｌ１∥ｌ２∥ｌ３，直线 ＡＣ 分别交 ｌ１、ｌ２、ｌ３ 于点 Ａ、Ｂ、Ｃ， 直线 ＤＦ分别交 ｌ１、ｌ２、ｌ３ 于点 Ｄ、Ｅ、Ｆ，ＡＢ＝３，ＢＣ＝５，ＤＥ＝ ２，则 ＥＦ＝　　　　． 第 １５题图 １５．我国古代数学著作《九章算术》中 有题如下：“今有勾五步，股 十二 步．问勾中容方几何？”其大意译 为：如图，在 Ｒｔ△ＡＢＣ中，∠ＡＣＢ＝ ９０°，ＢＣ＝５，ＡＣ＝１２，四边形 ＣＤＥＦ 是 Ｒｔ△ＡＢＣ的内接正方形，点 Ｄ、 Ｅ、Ｆ分别在边 ＢＣ、ＡＢ、ＡＣ上，则正 方形 ＣＤＥＦ边长为　　　　                                                             ． ８ １６．若在△ＡＢＣ内有一点 Ｄ，使得∠ＡＤＢ＝∠ＡＤＣ，ＡＤ ＝ａ，ＣＤ＝ｂ，则当 ＢＤ＝　　 　　 时，△ＡＢＤ与 △ＡＣＤ相似． 三、解答题：本题共 ９小题，共 ８６分．解答应写出文字 说明，证明过程或演算步骤．在答题卡的相应位置内 作答． １７．（８分）计算：槡 槡６× ２－槡２４ 槡８ ＋２ｃｏｓ３０°． １８．（８分）小玲为毕业联欢会设计了一个“配橙色” 的游戏，使用的是如图所示两个可以自由转动的 转盘，每个转盘被分成面积相等的若干个扇形， 不同扇形分别填涂颜色．分界线可忽略．游戏者 同时转动两个转盘，两个转盘停止转动时，若有 一个转盘的指针指向红色，另一个转盘的指针指 向黄色，则“配橙色”游戏成功，游戏者获胜．求游 戏者获胜的概率（用列表法或树状图说明）． 第 １８题图 １９．（８分）如图，在 ８×８的网格图中，△ＡＢＣ三个顶 点坐标分别为 Ａ（０，２）、Ｂ（－１，０）、Ｃ（２，－１）． （Ⅰ）以 Ｏ为位似中心，将△ＡＢＣ放大为△Ａ′Ｂ′Ｃ′， 使得△Ａ′Ｂ′Ｃ′与△ＡＢＣ的位似比为 ２∶１，请在网 格图中画出△Ａ′Ｂ′Ｃ′； （Ⅱ）直接写出（Ⅰ）中点 Ａ′、Ｂ′、Ｃ′的坐标． 第 １９题图 ２０．（８分）如图，一架遥控无人机在点 Ａ处测得某高 楼顶点 Ｂ的仰角为 ６０°，同时测得其底部点 Ｃ的 俯角为 ３０°，点 Ａ与点 Ｂ的距离为 ６０米，求这栋 楼高 ＢＣ的长． 第 ２０题图                                                                       ９ ２１．（８分）某钢铁厂第一个月生产钢铁 １００万吨，从 第二个月起改进技术增大产量，第三个月生产钢 铁 １３２万吨，若钢铁产量第三个月增长率是第二 个月增长率的 ２倍，求第二个月钢铁产量的增 长率． ２２．（１０分）求证：相似三角形对应高的比等于相似比． （请根据题意补全图形，写出已知、求证并证明） 第 ２２题图 ２３．（１０分）已知 ｘ１、ｘ２ 是关于 ｘ的一元二次方程 ｘ２ ＋ ３ｘ＋ｋ－３＝０的两个实数根． （Ⅰ）求 ｋ的取值范围； （Ⅱ）若 ｘ２ １ ＋２ｘ１ ＋ｘ２ ＋ｋ＝３，试求 ｋ的值． ２４．（１３分）如图，已知直线 ｙ＝３ ４ｘ＋ｂ与 ｘ轴、ｙ轴分 别交于点 Ｂ、Ａ．点 Ｐ是 ｙ轴上一动点，ＰＱ⊥ＡＢ于 点 Ｑ，点 Ａ的坐标为（０，３）． （Ⅰ）求直线 ＡＢ的解析式； （Ⅱ）若ＡＱ ＡＢ＝４ ５，求点 Ｐ的坐标； （Ⅲ）当点 Ｐ在 ｙ轴负半轴时，连接 ＢＰ、ＯＱ，分别 取 ＢＰ、ＯＱ的中点 Ｅ、Ｆ，连接 ＥＦ交 ＰＱ于点 Ｇ，当 ＯＱ∥ＢＰ时，求证：ＰＢ２ ＝２ＰＧ·ＰＱ． 第 ２４题图 ２５．（１３分）如图，在正方形 ＡＢＣＤ中，ＡＢ＝４，点 Ｐ、Ｑ 分别是 ＡＤ、ＡＣ边上的动点． （Ⅰ）填空：ＡＣ＝　　　　； （Ⅱ）若 ＡＰ＝３ＰＤ，且点 Ａ关于 ＰＱ的对称点 Ａ′落 在 ＣＤ边上，求 ｔａｎ∠Ａ′ＱＣ的值； （Ⅲ）设 ＡＰ＝ａ，直线 ＰＱ交 直 线 ＢＣ于 点 Ｔ，求 △ＡＰＱ与△ＣＴＱ面积之和 Ｓ的最小值（用含 ａ的 代数式表示）．                                                                       ０１ ２０１８－２０１９学年漳州上学期教学质量抽测 数学试卷 （考试时间：１２０分钟　满分：１５０分） 一、选择题（共 １０小题 ，每小题 ４分，满分 ４０分．每小 题只有一个正确的选项） １．方程 ｘ（ｘ－１）＝０的解是 Ａ．ｘ＝１　　　　　　　　　Ｂ．ｘ＝０ Ｃ．ｘ１ ＝１，ｘ２ ＝０ Ｄ．ｘ１ ＝－１，ｘ２ ＝０ ２．用配方法解一元二次方程 ｘ２ ＋４ｘ＋１＝０，下列变形 正确的是 Ａ．（ｘ－２）２ －３＝０ Ｂ．（ｘ＋４）２ ＝１５ Ｃ．（ｘ＋２）２ ＝５ Ｄ．（ｘ＋２）２ ＝３ ３．下列选项中，矩形具有的性质是 Ａ．四边相等 Ｂ．对角线互相垂直 Ｃ．对角线相等 Ｄ．每条对角线平分一组对角 ４．如图，直线 ｌ１∥ｌ２∥ｌ３，ＡＢ＝３，ＢＣ＝６，ＤＥ＝２，则 ＥＦ 的长是 Ａ．４　　　　Ｂ．５　　　　Ｃ．６　　　　Ｄ．７ 第 ４题图 　　　　 第 ６题图 ５．抛物线 ｙ＝（ｘ－１）２ ＋２的对称轴是 Ａ．直线 ｘ＝－１ Ｂ．直线 ｘ＝１ Ｃ．直线 ｘ＝２ Ｄ．直线 ｘ＝－２ ６．如图，过反比例函数 ｙ＝ｋ ｘ（ｘ＜０）图象上的一点 Ａ 作 ＡＢ⊥ｘ轴于点 Ｂ，连接 ＡＯ，若 Ｓ△ＡＯＢ ＝２，则 ｋ的 值是 Ａ．２ Ｂ．－２ Ｃ．４ Ｄ．－４ ７．将抛物线 ｙ＝３ｘ２ 先向左平移 １个单位长度，再向 上平移 ２个单位长度，所得抛物线的解析式是 Ａ．ｙ＝３（ｘ＋１）２ ＋２ Ｂ．ｙ＝３（ｘ－１）２ ＋２ Ｃ．ｙ＝３（ｘ－２）２ ＋１ Ｄ．ｙ＝３（ｘ－２）２ －１ ８．如图，ＢＤ⊥ＡＣ于点 Ｄ，ＣＥ⊥ＡＢ于点 Ｅ，ＢＤ与 ＣＥ 交于点 Ｏ，ＡＢ＝４，ＡＣ＝３，下列结论正确的是 第 ８题图 Ａ．ＡＤ ＡＥ＝３ ４ Ｂ．ＤＯ ＣＯ＝ＥＯ ＢＯ Ｃ．△ＡＢＤ的面积 △ＡＣＥ的面积 ＝４ ３ Ｄ．△ＡＢＤ的周长 △ＡＣＥ的周长 ＝１６ ９ ９．若点 Ａ（ｍ２，ｙ１），Ｂ（ｍ２ ＋２，ｙ２）在反比例函数 ｙ＝４ ｘ 的图象上，则 ｙ１，ｙ２ 的大小关系是 Ａ．ｙ１ ＞ｙ２ Ｂ．ｙ１ ＝ｙ２ Ｃ．ｙ１ ＜ｙ２ Ｄ．不能确定 第 １０题图 １０．如图，△ＡＢＣ∽ △ＡＤＥ， ∠ＢＡＣ＝∠ＤＡＥ＝９０°， ＡＢ与 ＤＥ交于点 Ｏ，ＡＢ ＝４，ＡＣ＝３，Ｆ是 ＤＥ的 中点，连 接 ＢＤ，ＢＦ，若 点 Ｅ是射线 ＣＢ上的动 点，下列 结 论：① △ＡＯＤ∽ △ＦＯＢ，② △ＢＯＤ∽ △ＥＯＡ，③∠ＦＤＢ＋∠ＦＢＥ＝９０°，④ＢＦ＝５ ６ＡＥ，其 中正确的是 Ａ．①② Ｂ．③ ④ Ｃ．②③ Ｄ．② ③④ 二、填空题（共 ６小题，每小题 ４分，满分 ２４分．请将 答案填入答题卡的相应横线上） １１．若 ｘ＝１是方程 ｘ２ ＋ｋｘ－４＝０的一个根，则 ｋ的值 是　　　　 １２．在菱形 ＡＢＣＤ中，对角线 ＡＣ＝２，ＢＤ＝４，菱形的周 长是　　　　 １３．若 ａ ２＝ｂ ３，则ａ＋２ｂ ａ ＝　　　　 第 １４题图 １４．如图，由边长为 １个单位长 度的小正方形组成的网格 中，先以点 Ｏ为位似中心， 将线段 ＡＢ放大为原来的 ２ 倍，得到线段 Ａ１Ｂ１（点 Ａ，Ｂ 的对应点分别为 Ａ１，Ｂ１）， 再将线段 Ａ１Ｂ１ 绕点 Ｂ１ 逆 时 针 旋 转 ９０°得 到 线 段 Ａ２Ｂ１，则四边形 ＡＡ１Ｂ１Ａ２ 的面积是　　　　个平 方单位． １５．函数 ｙ＝－ｘ２ ＋１，当 －１≤ｘ≤２时，函数 ｙ的最小 值是　　　　． 第 １６题图 １６．如 图，Ｒｔ△ＡＢＣ的 直 角 边 ＢＣ在 ｘ轴负半轴上，斜边 ＡＣ上的中线 ＢＤ的反向延 长线交 ｙ轴负半轴于点 Ｅ， 反比例函数 ｙ＝－２ ｘ（ｘ＜ ０）的图象过点 Ａ，则△ＢＥＣ 的面积是　　　　                                                                 ． １１ 三、解答题（共 ９题，满分 ８６分．请在答题卡的相应位 置作答） １７．（满分 ８分）解一元二次方程：２ｘ２ ＋４ｘ－１＝０． １８．（满分 ８分）如图，四边形 ＡＢＣＤ是正方形，Ｅ是 ＢＣ延长线上一点，且 ＡＣ＝ＥＣ．求∠ＤＡＦ的度数． 第 １８题图 １９．（满分 ８分）如图，已知 Ａ（ｍ，２），Ｂ（２，ｎ）是一次 函数 ｙ＝－ｘ＋１与反比例函数 ｙ＝ｋ ｘ（ｋ≠０）图象 的两个交点． （１）求反比例函数的解析式； （２）根据图象，请直接写出关于 ｘ的不等式 －ｘ＋ １＜ｋ ｘ的解集． 第 １９题图 ２０．（满分 ８分）求证：相似三角形对应角的角平分线 之比等于相似比． 要求：① 分 别 在 给 出 的 相 似 三 角 形 △ＡＢＣ与 △ＤＥＦ中用尺规作出一组对应角的平分线，不写 作法，保留作图痕迹； ②在完成作图的基础上，写出已知、求证，并加以 证明． 第 ２０题图 ２１．（满分 ８分）我国古代数学著作《九章算术》中记 载了一个问题：“今有邑方不知大小，各开中门， 出北门三十步有木，出西门七百五十步见木，问： 邑方几何？”．其大意是：如图，一座正方形城池，Ａ 为北门中点，从点 Ａ往正北方向走 ３０步到 Ｂ处 有一树木．Ｃ为西门中点，从点 Ｃ往正西方向走 ７５０步到 Ｄ处正好看到 Ｂ处的树木，求正方形城 池的边长． 第 ２１题图                                                                       ２１ ２２．（满分 １０分）已知：二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ（ａ≠ ０）中的 ｘ和 ｙ满足下表： ｘ … －１ ０ １ ２ ３ … ｙ … ３ ０ －１ ０ ｍ … （１）观察上表可求得 ｍ的值为　　　　； （２）试求出这个二次函数的解析式； （３）若点 Ａ（ｎ＋２，ｙ１），Ｂ（ｎ，ｙ２）在该抛物线上，且 ｙ１ ＞ｙ２，请直接写出 ｎ的取值范围． ２３．（满分 １０分）阳光市场某个体商户购进某种电子 产品，每个进价 ５０元，调查发现，当售价为 ８０元 时，平均一周可卖出 １６０个，而当售价每降低 ２元 时，平均一周可多卖出 ２０个，若设每个电子产品 降价 ｘ元． （１）根据题意，填表： 进价 （元） 售价 （元） 每件利 润（元） 销量 （个） 一周总 利润（元） 降价前 ５０ ８０ ３０ １６０ ３０×１６０ 降价后 ５０ （２）若商户计划每周盈利 ５２００元，且尽量减少库 存，则每个电子产品应降价多少元？ ２４．（满分 １２分）如图，把矩形 ＡＢＣＤ沿 ＡＣ折叠，使 点 Ｄ与点 Ｅ重合，ＡＥ交 ＢＣ于点 Ｆ，过点 Ｅ作 ＥＧ ∥ＣＤ交 ＡＣ于点 Ｇ，交 ＣＦ于点 Ｈ，连接 ＤＧ． （１）求证：四边形 ＥＣＤＧ是菱形； （２）若 ＤＧ＝６，ＡＧ＝１４ ５，求 ＥＨ的值． 第 ２４题图 ２５．（满分 １４分）已知：抛物线 ｙ＝ｍｘ２ ＋（ｍ－２）ｘ－ ２ｍ＋２（ｍ≠０）． （１）求证：抛物线与 ｘ轴有交点； （２）若抛物线与 ｘ轴交于点 Ａ（ｘ１，０），Ｂ（ｘ２，０），且 点 Ａ在点 Ｂ的右侧，ｘ１ ＋２ｘ２ ＝１． ①求 ｍ的值； ②点 Ｐ在抛物线上，点 Ｇ（ｎ，－４ ３ｎ－３５ ９），求 ＰＧ 的最小值                                                                       ． ３１ ２０１８－２０１９学年福建省莆田市九年级（上）期末数学试卷 一、选择题（每小题 ４分，共 ４０分） １．若一元二次方程 ｘ２ －ｘ－６＝０的两根为 ｘ１，ｘ２，则 ｘ１ ＋ｘ２ 的值为 （　　） Ａ．１　　　Ｂ．－１　　　Ｃ．０　　　Ｄ．－６ ２．用配方法解一元二次方程 ｘ２ ＋４ｘ－５＝０，此方程可 变形为 （　　） Ａ．（ｘ＋２）２ ＝９ Ｂ．（ｘ－２）２ ＝９ Ｃ．（ｘ＋２）２ ＝１ Ｄ．（ｘ－２）２ ＝１ ３．对于函数 ｙ＝４ ｘ，下列说法错误的是 （　　） Ａ．这个函数的图象位于第一、第三象限 Ｂ．这个函数的图象既是轴对称图形又是中心对 称图形 Ｃ．当 ｘ＞０时，ｙ随 ｘ的增大而增大 Ｄ．当 ｘ＜０时，ｙ随 ｘ的增大而减小 ４．一个不透明的袋中装有除颜色外其余均相同的 ５ 个红球和 ３个黄球，从中随机摸出一个，则摸到黄 球的概率是 （　　） Ａ．１ ８ Ｂ．１ ３ Ｃ．３ ８ Ｄ．３ ５ ５．如图，Ｄ、Ｅ、Ｆ分别是△ＡＢＣ的边 ＡＢ、ＢＣ、ＡＣ的中 点．若四边形 ＡＤＥＦ是菱形，则△ＡＢＣ必须满足的 条件是 （　　） 第 ５题图 Ａ．ＡＢ⊥ＡＣ Ｂ．ＡＢ＝ＡＣ Ｃ．ＡＢ＝ＢＣ Ｄ．ＡＣ＝ＢＣ ６．如果平行四边形的四个内角的平分线能够围成一 个四边形，那么这个四边形一定是 （　　） Ａ．平行四边形 Ｂ．矩形 Ｃ．菱形 Ｄ．正方形 ７．如图，直线 ＡＢ与⊙Ｏ相切于点 Ａ，⊙Ｏ的半径为 １， 若∠ＯＢＡ＝３０°，则 ＯＢ长为 （　　） 第 ７题图 槡Ａ．１ Ｂ．２ Ｃ． ３ Ｄ．２ ８．已知反比例函数 ｙ＝－６ ｘ，下列结论中不正确的是 （　　） Ａ．图象必经过点（－３，２） Ｂ．图象位于第二、四象限 Ｃ．若 ｘ＜－２，则 ０＜ｙ＜３ Ｄ．在每一个象限内，ｙ随 ｘ值的增大而减小 ９．抛物线图象如图所示，根据图象，抛物线的解析式 可能是 （　　） 第 ９题图 Ａ．ｙ＝ｘ２ －２ｘ＋３ Ｂ．ｙ＝－ｘ２ －２ｘ＋３ Ｃ．ｙ＝－ｘ２ ＋２ｘ＋３ Ｄ．ｙ＝－ｘ２ ＋２ｘ－３ １０．如图，晚上小亮在路灯下散步，在小亮由 Ａ处径 直走到 Ｂ处这一过程中，他在地上的影子（　　） 第 １０题图 Ａ．逐渐变短 Ｂ．先变短后变长 Ｃ．先变长后变短 Ｄ．逐渐变长 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．如图，已知直线 ａ∥ｂ∥ｃ，直线 ｍ，ｎ与直线 ａ，ｂ，ｃ 分别交于点 Ａ，Ｃ，Ｅ，Ｂ，Ｄ，Ｆ，若 ＡＣ＝４，ＣＥ＝６，ＢＤ ＝３，则 ＤＦ的值是　　　　． 第 １１题图 １２．一个不透明的袋中装有若干个红球，为了估计袋 中红球的个数，小文在袋中放入 １０个白球（每个 球除颜色外其余都与红球相同）．摇匀后每次随 机从袋中摸出一个球，记下颜色后放回袋中，通 过大量重复摸球试验后发现，摸到白球的频率是 ２ ７，则袋中红球约为　　　　个． １３．已知反比例函数 ｙ＝３ ｘ，ｘ＞０时，ｙ　　　　０，这 部分图象在第　　　　象限，ｙ随着 ｘ值的增大 而　　　　                                                                  ． ４１ １４．若式子 ５－槡 ｘ有意义，则 ｘ的取值范围是　　　． １５．如图，已知直线 ａ∥ｂ，∠１＝７０°，则∠２＝　　　． 第 １５题图 　　 第 １６题图 １６．如图，矩形 ＡＢＣＤ的对角线 ＡＣ和 ＢＤ相交于点 Ｏ， ∠ＡＤＢ＝３０°，ＡＢ＝４，则 ＯＣ＝　　　　． 三、解答题（共 ９小题，共 ８６分） １７．如图，在△ＡＢＣ中，ＣＤ是 ＡＢ边上的中线，Ｅ是 ＣＤ 的中点，过点 Ｃ作 ＡＢ的平行线交 ＡＥ的延长线于 点 Ｆ，连接 ＢＦ． （１）求证：ＣＦ＝ＡＤ； （２）若 ＣＡ＝ＣＢ，∠ＡＣＢ＝９０°，试判断四边形 ＣＤ ＢＦ的形状，并说明理由． 第 １７题图 １８．满洲里市某楼盘准备以每平方米 ５０００元的均价 对外销售，由于国务院有关房地产的新政策出台 后，购房者持币观望．为了加快资金周转，房地产 开发商对价格经过两次下调后，决定以每平方米 ４０５０元的均价开盘销售． （１）求平均每次下调的百分率； （２）某人准备以开盘均价购买一套 １００平方米的 房子．开发商还给予以下两种优惠方案以供选 择：①打 ９．８折销售；②不打折，送两年物业管理 费，物业管理费是每平方米每月 １．５元，请问哪种 方案更优惠？ １９．如图，已知△ＡＢＣ，∠ＢＡＣ＝９０°． （１）尺规作图：作 ＢＣ边的高 ＡＤ（保留作图痕迹， 第 １９题图 不写作法）； （２）求证：∠Ｃ＝∠ＢＡＤ． ２０．（１）在图①中画出△ＡＢＣ绕点 Ｏ顺时针旋转 ９０° 后的图形； （２）在图②中画出四边形 ＡＢＣＤ关于点 Ｏ对称的 图形． 第 ２０题图 ２１．某校举办篮球比赛，进入决赛的队伍有 Ａ、Ｂ、Ｃ、Ｄ 四队，要从中选出两队打一场比赛． （１）若已确定 Ａ打第一场，再从其余三队中随机 选取一队，求恰好选中 Ｄ队的概率； （２）请用画树状图或列表法，求恰好选中 Ｂ、Ｃ两 队进行比赛的概率                                                                       ． ５１ ２２．为进一步发展基础教育，自 ２０１４年以来，某县加 大了教育经费的投入，２０１４年该县投入教育经费 ６０００万元．２０１６年投入教育经费 ８６４０万元．假设 该县这两年投入教育经费的年平均增长率相同． （１）求 这 两 年 该 县 投 入 教 育 经 费 的 年 平 均 增 长率； （２）若该县教育经费的投入还将保持相同的年平 均增长率，请你预算 ２０１７年该县投入教育经费多 少万元． ２３．如图，ＡＢ表示路灯，ＣＤ、Ｃ′Ｄ′表示小明所在两个 不同位置： （１）分别画出这两个不同位置小明的影子； （２）小明发现在这两个不同的位置上，他的影子 长分别是自己身高的 １倍和 ２倍，他又量得自己 的身高为 １．５米，ＤＤ′长为 ３米，你能帮他算出路 灯的高度吗？（Ｂ、Ｄ、Ｄ′在一条直线上） 第 ２３题图 ２４．如图，在平面直角坐标系中，函数 ｙ＝ｋ ｘ的图象经 过点 Ｐ（４，３）和点 Ｂ（ｍ，ｎ）（其中 ０＜ｍ＜４），作 ＢＡ⊥ ｘ轴 于 点 Ａ，连 接 ＰＡ，ＰＢ，ＯＢ，已 知 Ｓ△ＡＯＢ ＝Ｓ△ＰＡＢ． （１）求 ｋ的值和点 Ｂ的坐标； （２）求直线 ＢＰ的解析式； （３）直接写出在第一象限内，使反比例函数大于 一次函数的 ｘ的取值范围是　　　　　　． 第 ２４题图 ２５．如图，在直角坐标系中，Ｒｔ△ＯＡＢ的直角顶点 Ａ 在 ｘ轴上，ＯＡ＝４，ＡＢ＝３．动点 Ｍ从点 Ａ出发，以 每秒 １个单位长度的速度，沿 ＡＯ向终点 Ｏ移动； 同时点 Ｎ从点 Ｏ出发，以每秒 １．２５个单位长度 的速度，沿 ＯＢ向终点 Ｂ移动．当两个动点运动了 ｘ秒（０＜ｘ＜４）时，解答下列问题： （１）求点 Ｎ的坐标（用含 ｘ的代数式表示）； （２）设△ＯＭＮ的面积是 Ｓ，求 Ｓ与 ｘ之间的函数 表达式；当 ｘ为何值时，Ｓ有最大值？最大值是 多少？ 第 ２５题图 （３）在两个动 点 运 动过 程 中，是否存在某一时刻，使 △ＯＭＮ是直角三角形？若 存在，求出 ｘ的值；若不存 在，请说明理由                                                                       ． ６１ 宁德市 ２０１８－２０１９学年度第一学期期末九年级质量检测 数学试题 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部 分，满分 １５０分． 注意事项： １．答题前，考生务必在试题卷、答题卡规定位置 填写本人准考证号、姓名等信息．考生要认真 核对答题卡上粘贴的条形码的“准考证号、姓 名”与考生本人准考证号、姓名是否一致． ２．选择题每小题选出答案后，用 ２Ｂ铅笔把答题 卡上对应题目的答案标号涂黑，如需改动，用 橡皮擦干净后，再选涂其他答案标号．非选择 题答案用 ０．５毫米黑色墨水签字笔在答题卡 上相应位置书写作答，在试题卷上答题无效． ３．作图可先使用 ２Ｂ铅笔画出，确定后必须用 ０．５ 毫米黑色墨水签字笔描黑． ４．考试结束，考生必须将试题卷和答题卡一并 交回． 第Ⅰ卷 一、选择题：本题共 １０小题，每小题 ４分，共 ４０分．在 每个小题给出的四个选项中，只有一项是符合题目要 求的． １．已知 ａ ｂ＝２ ５，则ａ＋ｂ ｂ 的值为 Ａ．２ ５　　　Ｂ．３ ５　　　Ｃ．２ ３　　　Ｄ．７ ５ ２．已知∠Ａ为锐角，若 ｓｉｎＡ＝１ ２，则∠Ａ的度数为 Ａ．３０° Ｂ．４５° Ｃ．６０° Ｄ．７５° ３．已知一个几何体如图所示，则该几何体的左视 图是 ４．一元二次方程 ｘ２ ＋２ｘ＝０的根的情况是 Ａ．有两个相等的实数根 Ｂ．有两个不相等的实数根 Ｃ．只有一个实数根 Ｄ．没有实数根 ５．为了估计抛掷同一枚啤酒瓶盖落地后凸面向上的 概率，小明做了大量重复试验．经过统计得到凸面 向上的次数为 ４２０次，凸面向下的次数为 ５８０次， 由此可估计抛掷这枚啤酒瓶盖落地后凸面向上的 概率约为 Ａ．０．４２ Ｂ．０．５０ Ｃ．０．５８ Ｄ．０．７２ ６．如图，网格中的两个三角形是位似图形，它们的位 似中心是 第 ６题图 Ａ．点 Ａ Ｂ．点 Ｂ Ｃ．点 Ｃ Ｄ．点 Ｄ ７．已知 Ｒｔ△ＡＢＣ，∠Ｃ＝９０°，若∠Ａ＞∠Ｂ，则下列选 项正确的是 Ａ．ｓｉｎＡ＜ｓｉｎＢ Ｂ．ｃｏｓＡ＜ｃｏｓＢ Ｃ．ｔａｎＡ＜ｔａｎＢ Ｄ．ｓｉｎＡ＜ｃｏｓＡ ８．如图，在△ＡＢＣ中，点 Ｄ，Ｅ，Ｆ分别是 ＡＢ，ＢＣ，ＡＣ的 中点，则下列四个判断中不一定正确的是 第 ８题图 Ａ．四边形 ＡＤＥＦ一定是平行四边形 Ｂ．若∠Ｂ＋∠Ｃ＝９０°，则四边形 ＡＤＥＦ是矩形 Ｃ．若四边形 ＡＤＥＦ是菱 形，则 △ＡＢＣ是等 边三 角形 Ｄ．若四边形 ＡＤＥＦ是正方形，则△ＡＢＣ是等腰直 角三角形 ９．已知 ｙ＝ａｘ２ ＋ｂｘ＋ｃ（ａ≠０）的部分图象如图所示， 若 ｘ１，ｘ２ 是一元二次方程 ａｘ２ ＋ｂｘ＋ｃ＝０的两个 根，且 ｘ１ ＜ｘ２，则下列说法正确的是 第 ９题图                                                                ７１ Ａ．４＜ｘ２ ＜５ Ｂ．１＜ｘ１ ＜２ Ｃ．ｂ２ －４ａｃ＜０ Ｄ．ｘ１ ＋ｘ２ ＝２ １０．下列每个“田”字中的数据都按相同的规律排列， 其最后一个“田”字中 ａ的值为 Ａ．７ Ｂ．８ Ｃ．９ Ｄ．１０ 第Ⅱ卷 注意事项： １．用 ０．５毫米黑色签字笔在答题卡相应位置书 写作答，在试题卷上答题无效． ２．作图可先用 ２Ｂ铅笔画出，确定后必须用 ０．５ 毫米黑色签字笔描黑． 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分． 第 １１题图 １１．广场上一个大型艺术字板块在 地上投影如图所示，则该投影 属于　　　　．（填写“平行投 影”或“中心投影”） １２．若 ｘ＝３是方程 ｘ２ －ｋｘ－６＝０的一个解，则方程 的另一个解是　　　　． １３．已知四边形 ＡＢＣＤ与四边形 ＥＦＧＨ相似，相似比 为 ２ ３，若四边形 ＡＢＣＤ的面积为 ３６ｃｍ２，则四边形 ＥＦＧＨ的面积为　　　　ｃｍ２． １４．在 Ｒｔ△ＡＢＣ中，∠Ｃ＝９０°，若 ｔａｎＡ＝２ ５，则 ｔａｎＢ＝ 　　　　． １５．已知二次函数的图象与抛物线 ｙ＝－２ｘ２ ＋３的开 口大小、方向完全相同，且顶点坐标为（２，－１）， 则该二次函数的表达式为　　　　． 第 １６题图 １６．如图，已知直线 ｌ：ｙ＝－１ ３ｘ ＋ｂ（ｂ＜０）与 ｘ，ｙ轴分别交 于 Ａ，Ｂ两点，以 ＡＢ为边在 直线 ｌ的上方作正方形 ＡＢ ＣＤ，反比例函数 ｙ１ ＝ｋ１ ｘ和 ｙ２ ＝ｋ２ ｘ的图象分别过点 Ｃ和点 Ｄ．若 ｋ１ ＝３，则 ｋ２ 的 值为　　　　． 三、解答题：本题有 ９小题，共 ８６分． １７．（本题满分 ７分） 解方程：ｘ２ －４ｘ＋１＝０． １８．（本题满分 ７分） 如图，已知△ＡＤＥ∽△ＡＢＣ，且 ＡＤ＝６，ＡＥ＝４，ＡＢ ＝１２，求 ＣＤ的长． 第 １８题图 １９．（本题满分 ８分） 某商场在促销活动中规定，顾客每消费 １００元就 能获得一次抽奖机会．为了活跃气氛，设计了两 个抽奖方案： 方案一：转动转盘 Ａ一次，转出红色可领取一份 奖品； 方案二：转动转盘 Ｂ两次，两次都转出红色可领 取一份奖品．（两个转盘都被平均分成 ３份） 如果你获得一次抽奖机会，你会选择哪个方案？ 请用相关的数学知识说明理由． 转盘 Ａ 　　 转盘 Ｂ 第 １９题图 ２０．（本题满分 ８分） 利用所给的图形证明：一个顶点到它所对的两边 距离相等的平行四边形是菱形．（写出已知、求证 并加以证明） 第 ２０题图 已知： 求证： 证明                                                                       ： ８１ ２１．（本题满分 １０分） 已知二次函数 ｙ＝ｘ２ ＋２ｘ＋２与反比例函数 ｙ＝ｋ ｘ （ｋ≠０）的图象都经过点 Ａ（１，ｍ）． （１）求反比例函数的表达式； （２）当二次函数与反比例函数的值都随 ｘ的增大 而减小时，求 ｘ的取值范围． ２２．（本题满分 １０分） 小颖根据网络图片，制作了一个如图①所示的手 机支架，图②是该支架的侧面示意图．已知靠板 ＡＢ的倾角∠ＡＢＣ＝６８°，支撑板 ＣＤ与靠板 ＡＢ的 夹角∠ＡＥＣ＝８７°，插孔 Ｅ与端点 Ｂ之间的线段 ＢＥ＝３ｃｍ，若支撑板上 ＤＥ部分的长为 ２ｃｍ，求支 撑板 ＣＤ的长．（结果精确到 ０．１ｃｍ） 温馨提示：ｓｉｎ６８°≈０．９２７，ｃｏｓ６８°≈０．３７５，ｔａｎ６８° ≈２．４７５，ｓｉｎ７１°≈０．９４６，ｃｏｓ７１°≈０．３２６，ｔａｎ７１°≈ ２．９０４． 图① 　　 图② 第 ２２题图 ２３．（本题满分 １０分） 某地特产槟榔芋深受欢迎，某商场以 ７元／千克 收购了 ３０００千克优质槟榔芋，若现在马上出售， 每千克可获得利润 ３元．根据市场调查发现，近 段时间内槟榔芋的售价每天上涨 ０．２元 ／千克，为 了获得更大利润，商家决定先贮藏一段时间后再 出售，根据以往经验，这批槟榔芋的贮藏时间不 宜超过 １００天，在贮藏过程中平均每天损耗约 １０ 千克． （１）若商家将这批槟榔芋贮藏 ｘ天后一次性出 售，请完成下列表格： 每千克槟 榔芋售价 （单位：元） 可供出售的 槟榔芋重量 （单位：千克） 现在出售 ３０００ ｘ天后出售 （２）将这批槟榔芋贮藏多少天后一次性出售最终 可获得总利润 ２９０００元？ ２４．（本题满分 １３分） 如图，矩形 ＡＢＣＤ中，ＢＣ＝１０，ＡＢ＝７，点 Ｐ在 ＣＤ 边上运动，将矩形 ＡＢＣＤ沿 ＢＰ折叠，使点 Ｃ落在 直线 ＡＤ上方的点 Ｇ处，ＢＧ，ＰＧ分别交边 ＡＤ于 点 Ｍ，Ｎ． （１）求证：△ＡＢＭ∽△ＤＮＰ； （２）当点 Ｇ与边 ＣＤ的距离为 ５时，求 ＣＰ的长； （３）连接 ＭＣ，在点 Ｐ的运动过程中，是否存在某 一点 Ｐ，使得△ＢＣＭ是等腰三角形？若存在，请 用尺规在作 图 区 内的 矩 形 中作 出所 有可 能的 △ＢＧＰ，并标出相应的字母；若不存在，请说明 理由． 第 ２４题图                                                                       ９１ ２５．（本题满分 １３分） 如图，已知抛物线 ｙ＝ａｘ２ ＋ｂｘ＋３（ａ≠０）与 ｘ轴交 于 Ａ（－４，０），Ｂ（６，０）两点，与 ｙ轴交于点 Ｃ．若 Ｇ 是该抛物线上 Ａ，Ｃ之间的一个动点，过点 Ｇ作直 线 ＧＤ∥ｘ轴，交抛物线于点 Ｄ，过点 Ｄ，Ｇ分别作 ｘ 轴的垂线，垂足分别为 Ｅ，Ｆ，得到矩形 ＤＥＦＧ． （１）求该抛物线的表达式； （２）当点 Ｇ与点 Ｃ重合时，求矩形 ＤＥＦＧ的面积； （３）若 直 线 ＢＣ分 别 交 ＤＧ，ＤＥ于 点 Ｍ，Ｎ，求 △ＤＭＮ面积的最大值． 第 ２５题图 ０２ ２０１８－２０１９年龙岩第一学期期末质量检查 九年级　数学试题 （考试时间：１２０分钟；满分 １５０分） 　　　　 　 　　 　　　　　　　 　　一、选择题（本大题共 １０题，每小题 ４分，共 ４０分） １．下列图形中，既是中心对称图形，又是轴对称图形 的是 （　　） ２．下列关于事件发生可能性的表述，正确的是 （　　） Ａ．事件：“在地面，向上抛石子后落在地上”，该事 件是随机事件 Ｂ．体育彩票的中奖率为 １０％，则买 １００张彩票必 有 １０张中奖 Ｃ．掷两枚硬币，朝上的一面是一正面一反面的概 率为 １ ３ Ｄ．在同批次 １００００件产品中抽取 １００件发现有 ５ 件次品，则这批产品中大约有 ５００件左右的 次品 ３．抛物线 ｙ＝３（ｘ－２）２ ＋５的顶点坐标是 （　　） Ａ．（－２，５） Ｂ．（－２，－５） Ｃ．（２，５） Ｄ．（２，－５） ４．关于 ｘ的一元二次方程 ｘ２ ＋４ｘ＋ｋ＝０有两个实数 根，则 ｋ的取值范围是 （　　） Ａ．ｋ≤４ Ｂ．ｋ＜－４ Ｃ．ｋ≤ －４ Ｄ．ｋ＜４ ５．以 ２和 ４为根的一元二次方程是 （　　） Ａ．ｘ２ ＋６ｘ＋８＝０ Ｂ．ｘ２ －６ｘ＋８＝０ Ｃ．ｘ２ ＋６ｘ－８＝０ Ｄ．ｘ２ －６ｘ－８＝０ ６．如 图，ＡＢ是 ⊙Ｏ的 直 径，点 Ｃ，Ｄ在 ⊙Ｏ上．若 第 ６题图 ∠ＡＣＤ＝２５°，则 ∠ＢＯＤ 的 度 数为 （　　） Ａ．１００° Ｂ．１２０° Ｃ．１３０° Ｄ．１５０° ７．有 ｎ支球队参加篮球比赛，共比赛了 １５场，每两个 队之间只比赛一场，则下列方程中符合题意的是 （　　） Ａ．ｎ（ｎ－１）＝１５ Ｂ．ｎ（ｎ＋１）＝１５ Ｃ．ｎ（ｎ－１）＝３０ Ｄ．ｎ（ｎ＋１）＝３０ ８．如图，ＰＡ，ＰＢ，ＣＤ分别切于 Ａ，Ｂ，Ｅ，ＣＤ交 ＰＡ，ＰＢ 于 Ｃ，Ｄ两点，若∠Ｐ＝４０°，则∠ＰＡＥ＋∠ＰＢＥ的度 数为 （　　） Ａ．５０° Ｂ．６２° Ｃ．６６° Ｄ．７０° 第 ８题图 　　 第 ９题图 ９．如图，在面积为 １２的平行四边形 ＡＢＣＤ中，对角线 ＢＤ绕着它的中点 Ｏ按顺时针方向旋转一定角度 后，其所在直线分别交 ＡＢ，ＣＤ于点 Ｅ，Ｆ，若 ＡＥ＝ ２ＥＢ，则图中阴影部分的面积等于 （　　） Ａ．２ Ｂ．１ Ｃ．４ ３ Ｄ．２ ３ １０．如图，边长为 ２的正△ＡＢＣ的边 ＢＣ在直线 ｌ上， 两条距离为 １的平行直线 ａ和 ｂ垂直于直线 ｌ，ａ 和 ｂ同时向右移动（ａ的起始位置在 Ｂ点），速度 均为每秒 １个单位，运动时间为 ｔ（秒），直到 ｂ到 达 Ｃ点 停止，在 ａ和 ｂ向右 移动 的过 程 中，记 △ＡＢＣ夹在 ａ和 ｂ之间的部分的面积为 Ｓ，则 Ｓ关 于 ｔ的函数图象大致为 （　　） 二、填空题（本大题共 ６题，每小题 ４分，共 ２４分） １１．九（５）班有男生 ２７人，女生 ２３人，班主任发放准 考证时，任意抽取一张准考证，恰好是女生的准考 证的概率是　　　　． １２．已知扇形所在圆半径为 ４，弧长为 ６π，则扇形面积 为　　　　． １３．已知点 Ａ（１，３），Ｏ是坐标原点，将线段 ＯＡ绕点 Ｏ 逆时针旋转 ９０°，点 Ａ旋转后的对应点是 Ａ１，则点 Ａ１ 的坐标是　　　　                                                               ． １２ １４．把抛物线 ｙ＝２ｘ２ 先向下平移 １个单位，再向左平 移 ２个单位，得到的抛物线的解析式是　　　　． １５．《九章算术》“勾股”章有一题：“今有户高多于广 六尺，两隅相去适一丈，问户高、广各几何？”大意 是说：已知矩形门的高比宽多 ６尺，门的对角线长 １丈，那么门的高和宽各是多少？（１丈 ＝１０尺）， 如果设门的宽为 ｘ尺，那么这个门的高为（ｘ＋６） 尺，根据题意得方程：　　　　　　　　． １６．已知函数 ｙ１ ＝（ａ２ ＋１）ｘ２ ＋ｂｘ＋ｃ，ｙ２ ＝－ｘ＋２，若 方程（ａ２ ＋１）ｘ２ ＋（ｂ＋１）ｘ＋ｃ－２＝０的两根分别 为 ｘ１ ＝－２，ｘ２ ＝８，则使 ｙ１ ＞ｙ２ 成立的 ｘ的取值范 围是　　　　　　． 三、解答题（本大题共 ９小题，共 ８６分） １７．（８分）解方程：ｘ２ ＋２ｘ＝１ １８．（８分）在如图所示的直角坐标系中，解答下列 问题： （１）将△ＡＢＣ绕点 Ａ顺时针旋转 ９０°，画出旋转后 的△ＡＢ１Ｃ１； （２）将△ＡＢＣ绕点 Ａ顺时针旋转 ９０°后，求出点 Ｂ 旋转到 Ｂ１ 所经过的路径长． 第 １８题图 １９．（８分）先化简，再求值：（２ｘ＋１ ｘ －１）÷ｘ２ －１ ｘ ， 其中 ｘ 槡＝ ２＋１． ２０．（８分）一个不透明的口袋里装有分别标有汉字 “美”、“丽”、“龙”、“岩”的四个小球，除汉字不同 之外，小球没有任何区别，每次摸球前先搅拌均匀 再摸球． （１）若从中任取一个球，求摸出球上的汉字刚好 是“美”的概率； （２）若从中任取一个球，不放回，再从中任取一个 球，请用树状图或列表法，求取出的两个球上的汉 字恰能组成“美丽”或“龙岩”的概率． ２１．（８分）如图，⊙Ｏ为锐角△ＡＢＣ的外接圆，半径 为 ５． （１）用尺规作图作出∠ＢＡＣ的平分线，并标出它 与劣弧 ) ＢＣ的交点 Ｅ（保留作图痕迹，不写作法）； （２）若（１）中的点 Ｅ到弦 ＢＣ的距离为 ３，求弦 ＣＥ 的长． 第 ２１题图                                                                       ２２ ２２．（１０分）某种蔬菜的销售单价 ｙ１ 与销售月份 ｘ之 间的关系如图①所示，成本 ｙ２ 与销售月份 ｘ之间 的关系如图②所示． （１）已知 ６月份这种蔬菜的成本最低，此时出售 每千克的收益是多少元？（收益 ＝售价 －成本） （２）分别求出 ｙ１，ｙ２ 与 ｘ之间的函数关系式； （３）哪个月出售这种蔬菜，每千克的收益最大？ 说明理由． 第 ２２题图 ２３．（１０分）如图，在△ＡＢＣ中，∠Ｃ＝９０°，点 Ｏ在 ＡＣ 上，以 ＡＯ为半径的⊙Ｏ交 ＡＢ于 Ｄ，ＢＤ的垂直平 分线交 ＢＤ于 Ｆ，交 ＢＣ于 Ｅ，连接 ＤＥ． （１）求证：ＤＥ是⊙Ｏ的切线； （２）若∠Ｂ＝３０°，ＢＣ 槡＝４ ３，且 ＡＤ∶ＤＦ＝１∶３，求 ⊙Ｏ的直径． 第 ２３题图                                                                       ３２ ２４．（１２分）数学兴趣小组活动中，小明进行数学探究 活动．将边长为槡２的正方形 ＡＢＣＤ与边长为槡５的 正方形 ＡＥＦＧ按图①位置放置，ＡＤ与 ＡＥ在同一 条直线上，ＡＢ与 ＡＧ在同一条直线上． （１）小明发现 ＤＧ⊥ＢＥ，请你帮他说明理由． （２）如图②，小明将正方形 ＡＢＣＤ绕点 Ａ逆时针旋 转，当点 Ｂ恰好落在线段 ＤＧ上时，请你帮他求出 此时 ＢＥ的长． 图① 　　 图② 　第 ２４题图 ２５．（１４分）在平面直角坐标系 ｘＯｙ中，已知抛物线 ｙ＝ ａｘ２ ＋ｂｘ＋３（ａ≠０）经过点 Ａ（－２，３）． （１）若点 Ｂ（１，０）也在此抛物线上， ①求该抛物线的解析式； ②若点 Ｐ是一个该抛物线位于线段 ＡＢ上方部分 的动点，当△ＰＡＢ的面积最大时，求点 Ｐ的坐标． （２）若抛物线 ｙ＝ａｘ２ ＋ｂｘ＋３与线段 ＡＢ有两个不 同的交点，求 ａ的取值范围                                                                       ． ４２ 三明市 ２０１８－２０１９学年上学期期末初中毕业班质量检测 数 学 试 题 一、选择题（共 １０题，每题 ４分，满分 ４０分．每题只有 一个正确选项） １．方程 ｘ２ ＝３ｘ的解是 （　　） Ａ．ｘ＝０　　　　　　　　　　Ｂ．ｘ＝３ Ｃ．ｘ＝０，ｘ＝３ Ｄ．ｘ＝０，ｘ＝－３ ２．如图，这个几何体的左视图是 （　　） 第 ２题图 ３．菱形的两条对角线长分别为 ６，８，则它的周长是 （　　） Ａ．５　 　 　Ｂ．１０　 　 　Ｃ．２０　 　 　Ｄ．２４ ４．九（１）班的教室里正在召开 ５０人的座谈会，其中有 ３名教师，１２名家长，３５名学生，当林校长走到教 室门口时，听到里面有人在发言，那么发言人是家 长的概率为 （　　） Ａ．７ １０ Ｂ．６ ２５ Ｃ．３ ５０ Ｄ．１ ３ ５．要制作两个形状相同的三角形框架，其中一个三角 形的边长分别为 ５ｃｍ，６ｃｍ和 ９ｃｍ，另一个三角形 的最短边长为 ２．５ｃｍ，则它的最长边为 （　　） Ａ．３ｃｍ Ｂ．４ｃｍ Ｃ．４．５ｃｍ Ｄ．５ｃｍ ６．将二次函数 ｙ＝ｘ２ －４ｘ＋３通过配方可化为 ｙ＝ａ（ｘ －ｈ）２ ＋ｋ的形式，结果为 （　　） Ａ．ｙ＝（ｘ－２）２ －１ Ｂ．ｙ＝（ｘ－２）２ ＋３ Ｃ．ｙ＝（ｘ＋２）２ ＋３ Ｄ．ｙ＝（ｘ＋２）２ －１ ７．对于反比例函数 ｙ＝－２ ｘ，下列说法中不正确的是 （　　） Ａ．图象分布在第二，四象限 Ｂ．当 ｘ＞０时，ｙ随 ｘ的增大而增大 Ｃ．图象经过点（１，－２） Ｄ．若点 Ａ（ｘ１，ｙ１），Ｂ（ｘ２，ｙ２）都在图象上，且 ｘ１ ＜ ｘ２，则 ｙ１ ＜ｙ２ ８．一件商品的原价是 １００元，经过两次提价后的价格 是 １２１元，如果每次提价的百分率都是 ｘ，根据题 意，下面列出的方程正确的是 （　　） Ａ．１００（１－ｘ）＝１２１ Ｂ．１００（１＋ｘ）＝１２１ Ｃ．１００（１－ｘ）２ ＝１２１ Ｄ．１００（１＋ｘ）２ ＝１２１ ９．二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ与 一次函数 ｙ＝ａｘ＋ｃ在 同一直角坐标系中的图象大致是 （　　） １０．表中所列 ｘ，ｙ的 ７对值是二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ 图象上的点所对应的坐标，其中 ｘ１ ＜ｘ２ ＜ｘ３ ＜ｘ４ ＜ ｘ５ ＜ｘ６ ＜ｘ７． ｘ … ｘ１ ｘ２ ｘ３ ｘ４ ｘ５ ｘ６ ｘ７ … ｙ … ７ ｍ １４ ｋ １４ ｍ ７ … 根据表中提供的信息，有以下 ４个判断： ①ａ＜０；②７＜ｍ＜１４；③当 ｘ＝ｘ２ ＋ｘ６ ２ 时，ｙ的值是 ｋ；④ ｂ２≥４ａ（ｃ－ｋ）． 其中判断正确的是 （　　） Ａ．①②③ Ｂ．①②④ Ｃ．①③④ Ｄ．②③④ 二、填空题（共 ６题，每题 ４分，满分 ２４分） １１．方程 ｘ２ －９＝０的解是　　　　． １２．若 ｙ ｘ＝２ ３ ，则 ｘ＋ｙ ｘ 的值为　　　　． １３．如图，在小孔成像问题中，小孔 Ｏ到物体 ＡＢ的距 离是 ６０ｃｍ，小孔 Ｏ到像 ＣＤ的距离是 ３０ｃｍ，若物 体 ＡＢ的长为 １６ｃｍ，则像 ＣＤ的长是　 　 　ｃｍ． 第 １３题图 第 １４题图 １４．如图，在平面直角坐标系中， 点 Ａ是函数 ｙ＝ｋ ｘ（ｘ＜０）图 象上的点，ＡＢ⊥ｘ轴，垂足为 Ｂ，若 △ＡＢＯ的面积为 ３，则 ｋ 的值为　　　　                                                                 ． ５２ １５．如图，正方形 ＯＡＢＣ与正方形 ＯＤＥＦ是位似图，点 Ｏ为位似中心，位似比为 ２∶３，点 Ａ的坐标为（０， ２），则点 Ｅ的坐标是　　　　． １６．如图，Ｏ为 矩 形 ＡＢＣＤ对 角 线 ＡＣ，ＢＤ的 交 点， ＡＢ＝６，Ｍ，Ｎ是直线 ＢＣ上的动点，且 ＭＮ＝２，则 ＯＭ＋ＯＮ的最小值是　　　　． 第 １５题图 　　　 第 １６题图 三、解答题（共 ９题，满分 ８６分） １７．（本题满分 ８分） 已知关于 ｘ的一元二次方程 ｘ２ －２ｘ＋ｍ２ －ｍ＝０ 有两个相等的实数根，求 ｍ的值． １８．（本题满分 ８分） 第 １８题图 如图，是由 ６个棱长相同的小正 方体组合成的几何体． （１）请在下面方格纸中分别画出 它的主视图和俯视图； （２）如果在这个几何体上再添加 一些相同的小正方体，并保持这个几何体的主视 图和俯视图不变，那么请在下面方格纸中画出添 加小正方体后所得几何体可能的左视图（画出一 种即可） １９．（本题满分 ８分） 一个不透明的袋子中装有红、白两种颜色的小球， 这些球除颜色外完全相同，其中红球 １个，若从中 随机摸出一个球，这个球是白球的概率为 ２ ３． （１）求袋子中白球的个数； （２）随机摸出一个球后，放回并搅匀，再随机摸出 一个球，请用画树状图或列表的方法，求两次都摸 到白球的概率． ２０．（本题满分 ８分） 如图，在 Ｒｔ△ＡＢＣ中，∠ＡＣＢ＝９０°，ＣＤ⊥ＡＢ，垂足 为 Ｄ，ＢＥ⊥ＡＢ，垂足为 Ｂ，ＢＥ＝ＣＤ，连接 ＣＥ，ＤＥ． （１）求证：四边形 ＣＤＢＥ是矩形； （２）若 ＡＣ＝２，∠ＡＢＣ＝３０°，求 ＤＥ的长． 第 ２０题图                                                                       ６２ ２１．（本题满分 ８分） 如图，△ＡＢＣ中，ＡＢ＝８，ＡＣ＝６． （１）请用尺规作图的方法在 ＡＢ上找点 Ｄ，使得 △ＡＣＤ∽△ＡＢＣ；（保留作图痕迹，不写作法） （２）在（１）的条件下，求 ＡＤ的长． 第 ２１题图 ２２．（本题满分 １０分） 某百货商店服装柜在销售中发现，某品牌童装平 均每天可售出 ２０件，每件利润 ４０元，经市场调查 发现，在进货价不变的情况下，若每件童装每降价 １元，日销售量将增加 ２件． （１）若想要这种童装销售利润每天达到 １２００元， 同时又能让顾客得到更多的实惠，每件童装应降 价多少元？ （２）当每件童装降价多少元时，这种童装一天的 销售利润最多？最多利润是多少？ ２３．（本题满分 １０分） 如图，正方形 ＡＢＣＤ的顶点 Ａ在 ｘ轴的正半轴上， 顶点 Ｃ在 ｙ轴的正半轴上，点 Ｂ在双曲线 ｙ＝ －４ ｘ（ｘ＜０）上，点 Ｄ在双曲线 ｙ＝ｋ ｘ（ｘ＞０）上， 点 Ｄ的坐标是 （３，３）． 第 ２３题图 （１）求 ｋ的值； （２）求点 Ａ和点 Ｃ的坐标                                                                       ． ７２ ２４．（本题满分 １２分） 如图①，四边形 ＡＢＣＤ与四边形 ＣＥＦＧ都是矩形， 点 Ｅ，Ｇ分别在边 ＣＤ，ＣＢ上，点 Ｆ在 ＡＣ上，ＡＢ＝ ３，ＢＣ＝４． （１）求ＡＦ ＢＧ的值； （２）把矩形 ＣＥＦＧ绕点 Ｃ顺时针旋转到图②的位 置，Ｐ为 ＡＦ，ＢＧ的交点，连接 ＣＰ． （Ⅰ）求 ＡＦ ＢＧ的值． （Ⅱ）判断 ＣＰ与 ＡＦ的位置关系，并说明理由． 第 ２４题图 ２５．（本题满分 １４分） 已知抛物线 Ｃ：ｙ１ ＝ａ（ｘ－ｈ）２ ＋２，直线 ｌ：ｙ２ ＝ｋｘ －ｋｈ＋２（ｋ≠０）． （１）求证：直线 ｌ恒过抛物线 Ｃ的顶点； （２）若 ａ＞０，ｈ＝１，当 ｔ≤ｘ≤ｔ＋３时，二次函数 ｙ１ ＝ａ（ｘ－ｈ）２ ＋２的最小值为 ２，求 ｔ的取值范围； （３）点 Ｐ为抛物线的顶点，Ｑ为抛物线与直线 ｌ的 另一个交点，当 １≤ｋ≤３时，若线段 ＰＱ（不含端点 Ｐ，Ｑ）上至少存在一个横坐标为整数的点，求 ａ的 取值范围                                                                       ． ８２ 南平市 ２０１８－２０１９学年第一学期九年级 期末质量检测数学试题 （满分：１５０分；考试时间：１２０分钟） ★友情提示：①所有答案都必须填在答题卡相应的位 置上，答在本试卷上一律无效； ②试题未要求对结果取近似值的，不得 采取近似计算． 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分． 每小题只有一个正确的选项，请在答题卡 獉獉獉 的相应位置 填涂） １．下列图形中，既是轴对称图形又是中心对称图形 的是 （　　） ２．用配方法解方程 ｘ２ －２ｘ－１＝０，配方结果正确的 是 （　　） Ａ．（ｘ－２）２ ＝２　　　　　　　Ｂ．（ｘ－１）２ ＝２ Ｃ．（ｘ＋１）２ ＝２ Ｄ．（ｘ－１）２ ＝０ ３．同时抛掷两枚质地均匀的正方体骰子，每个骰子 的六个面分别标有 １，２，３，４，５，６这六个点数，下列 事件为必然事件的是 （　　） Ａ．朝上一面点数之和为 １２ Ｂ．朝上一面点数之和等于 ６ Ｃ．朝上一面点数之和小于 １３ Ｄ．朝上一面点数之和小于等于 ６ ４．如图，点 Ａ，Ｂ，Ｃ在⊙Ｏ上，过点 Ｃ作⊙Ｏ的切线与 ＯＡ的延长线交于点 Ｄ，若∠Ｄ＝３２°，则∠Ｂ的大小 为 （　　） Ａ．５８°　　　Ｂ．３４°　　　Ｃ．３２°　　　Ｄ．２９° 第 ４题图 ５．关于二次函数 ｙ＝（ｘ＋１）２ －２的图象，下列说法正 确的是 （　　） Ａ．对称轴是 ｘ＝１ Ｂ．开口向下 Ｃ．顶点坐标是（１，－２） Ｄ．与 ｘ轴有两个交点 ６．１２７５年我国南宋数学家杨辉提出一个问题：直田 积（矩形面积）八百六十四步（平方步），只云阔 （宽）不及长一十二步（宽比长少一十二步），问阔 及长各几步，设阔（宽）为 ｘ步，则所列方程正确的 是 （　　） Ａ．ｘ（ｘ＋１２）＝８６４ Ｂ．ｘ（ｘ－１２）＝８６４ Ｃ．（ｘ－１２）（ｘ＋１２）＝８６４ Ｄ．１２ｘ＝８６４ ７．已知⊙Ｏ的半径为 ５，直线 ｌ与⊙Ｏ相交，点 Ｏ到直 线 ｌ的距离为 ３，则⊙Ｏ上到直线 ｌ距离为 ２的点 共有 （　　） Ａ．１个 Ｂ．２个 Ｃ．３个 Ｄ．４个 ８．如果点 Ａ（－３，ｙ１），Ｂ（－２，ｙ２），Ｃ（２，ｙ３）都在反比 例函数 ｙ＝ｋ ｘ（ｋ＞０）的图象上，那么 ｙ１，ｙ２，ｙ３ 的大 小关系正确的是 （　　） Ａ．ｙ３ ＜ｙ２ ＜ｙ１ Ｂ．ｙ２ ＜ｙ１ ＜ｙ３ Ｃ．ｙ１ ＜ｙ２ ＜ｙ３ Ｄ．ｙ１ ＜ｙ３ ＜ｙ２ ９．若正方形的边长为 ４，则其外接圆半径与内切圆半 径的大小分别为 （　　） 槡Ａ．２ ２，２ Ｂ．４，２ Ｃ．４， 槡 槡２ ２ Ｄ．４ ２， 槡２ ２ １０．已知 ｋ为非零的实数，则抛物线 ｙ＝ｘ２ －２ｋｘ＋ｋ２ ＋１ ｋ的顶点 （　　） Ａ．在一条直线上 Ｂ．在某双曲线上 Ｃ．在一条抛物线上 Ｄ．无法确定 二、填空题（本大题共 ６小题，每空 ４分，共 ２４分．将 答案填入答题卡獉獉獉 的相应位置） １１．一元二次方程 ｘ２ ＝２的根是　　　　． １２．在一个不透明的口袋内只装有一些除颜色外完 全相同的红球、白球和黑球，从中任意摸出一个 球，摸到红球的概率是 ０．３，摸到白球的概率是 ０．４，那么摸到黑球的概率是　　　　． １３．若点 Ｐ（ｍ，－３）与点 Ｑ（２，ｎ）关于原点对称，则 ｍ ＋ｎ＝　　　　． １４．一个扇形的圆心角为 ８０°，面积是 ２πｃｍ２，则此扇 形的半径是　　　　 ｃｍ． １５．已知反比例函数 ｙ＝ｋ ｘ（ｋ≠０），当 １≤ｘ≤２时，函数 的最大值与最小值之差是 １，则 ｋ的值为　　　　． １６．如图，四边形 ＡＢＣＤ中，ＡＢ＝ＡＣ＝ＡＤ，若∠ＢＡＣ＝ ３９°，则∠ＢＤＣ＝　　　　°． 第 １６题图                                                                ９２ 三、解答题（本大题共 ９小题，共 ８６分．在答题卡 獉獉獉 的相 应位置作答） １７．解方程（每小题 ４分，共 ８分） （１）ｘ２ ＝２ｘ；　　　　（２）ｘ２ －５ｘ－５＝０． １８．（８分）已知关于 ｘ的一元二次方程 ｘ２ ＋３ｘ＋ｍ＝ ０有两个不相等的实数根，且 ｍ为正整数，求 ｍ 的值． １９．（８分）某中学食堂开设了两个窗口，窗口一提供 四种食品：肉包、馒头、鸡蛋、油饼；窗口二提供两 种食品：牛奶、豆浆．约定：学生在一个窗口领一 种食品后，再到另一个窗口领一种食品． （１）问：学生早餐领到的食品一共有几种不同的 可能？ （２）如果某天食堂师傅在两个窗口随机发放食 品，请用列表或画树状图的方法，求出小王同学 该天早餐刚好得到牛奶和馒头的概率． ２０．（８分）如图，△ＡＰＢ内接于⊙Ｏ． （１）作∠ＡＰＢ的平分线 ＰＣ，交⊙Ｏ于点 Ｃ（尺规 作图，保留作图痕迹，不写作法）； （２）在（１）的条件下，若∠ＡＰＢ＝１２０°，连接 ＡＣ， ＢＣ，求证：△ＡＢＣ是等边三角形． 第 ２０题图 ２１．（８分）如图，用 ４８米篱笆围成一个外形为矩形的 花园，花园一面利用院墙，中间用一道篱笆间隔 成两个小矩形，院墙的长度为 ２０米，平行于院墙 的一边长为 ｘ米，花园的面积为 Ｓ平方米． （１）求 Ｓ与 ｘ之间的函数关系式； （２）问花园面积可以达到 １８０平方米吗？如果 能，花园的长和宽各是多少？如果不能，请说明 理由． 第 ２１题图 ２２．（１０分）如图，ＡＢ是半圆 Ｏ的直径，点 Ｄ是半圆 上一点，连接 ＯＤ，ＡＥ⊥ＯＤ于点 Ｅ，设∠ＡＯＥ＝α， 将△ＡＥＯ绕点 Ｏ顺时针旋转 α角，得到△ＤＨＯ， 若点 Ｄ，Ｈ，Ｂ在一条直线上，求 α的值． 第 ２２题图 ２３．（１０分）如图，直线 ｙ＝ｋｘ（ｋ＜０）与反比例函数 ｙ ＝ｍ ｘ（ｍ＜０，ｘ＜０）的图象交于点 Ａ，直线与 ｙ轴 正半轴的夹角为 ６０°，ＯＡ＝２． （１）求反比例函数的解析式； （２）根据图象直接写出 ｍ ｘ＞ｋｘ的自变量的取值 范围． 第 ２３题图                                                                       ０３ ２４．（１２分）如图，在边长为 ８的等边△ＡＢＣ中，点 Ｄ 是 ＡＢ的中点，点 Ｅ是平面上一点，且线段 ＤＥ＝ ２，将线段 ＥＢ绕点 Ｅ顺时针旋转 ６０°得到线段 ＥＦ，连接 ＡＦ． （１）如图①，当 ＢＥ＝２时，求线段 ＡＦ的长； （２）如图②，①求证：ＡＦ＝ＣＥ； ②求线段 ＡＦ的取值范围． ２５．（１４分）我们把（ａ，ｂ，ｃ）称为抛物线 ｙ＝ａｘ２ ＋ｂｘ＋ ｃ的三维特征值．已知抛物线 ｙ１ 所对应的三维特 征值为（－１ ３，ｂ，０），且顶点在直线 ｘ＝２上． （１）求抛物线 ｙ１ 的解析式； （２）若直线 ｙ＝ｔ与抛物线 ｙ１ 交于点 Ｐ、Ｑ两点，当 １＜ＰＱ≤２时，求 ｔ的取值范围； （３）已知直线 ｘ＝２与 ｘ轴交于点 Ａ，将抛物线 ｙ１ 向右平移（槡３＋１）个单位得到抛物线 ｙ２，且抛物 线 ｙ２ 与直线 ｙ＝１分别相交于 Ｍ、Ｎ两点（Ｍ点在 Ｎ点的左侧），与 ｘ轴交于 Ｃ、Ｄ两点（Ｃ点在 Ｄ点 的左侧），求证：射线 ＡＮ平分∠                                          ＭＡＤ． １３ 书书书 ２０１８～２０１９学年度福州市九年级第一学期质量调研 数学试卷答案及评分标准 一、选择题（共 １０小题，每小题 ４分，满分 ４０分；在每小题给 出的四个选项中，只有一项是符合题目要求的，请在答题 卡的相应位置填涂） １．Ｄ　２．Ｄ　３．Ａ　４．Ｄ　５．Ｂ　６．Ｃ　７．Ａ　８．Ｂ　９．Ｃ １０．Ｂ 二、填空题（共 ６小题，每小题 ４分，满分 ２４分，请在答题卡的 相应位置作答） １１．１ ４　１２．－３　１３．８π ３　１４．３５ １５．π（ｘ ２ ＋３）２ －ｘ２ ＝７２　１６．槡３－１ 三、解答题（共 ９小题，满分 ８６分，请在答题卡的相应位置作 答） １７．解法一： ｘ２ ＋４ｘ＝－２， （１分）!!!!!!!!!!!!!!! ｘ２ ＋４ｘ＋２２ ＝－２＋２２， （３分）!!!!!!!!!!! （ｘ＋２）２ ＝２． （４分）!!!!!!!!!!!!!!! ｘ 槡＋２＝± ２， ｘ 槡＝－２± ２， （６分）!!!!!!!!!!!!!!! 即 ｘ１ 槡＝－２＋ ２，ｘ２ 槡＝－２－ ２． （８分）!!!!!!!! 解法二： ａ＝１，ｂ＝４，ｃ＝２． （１分）!!!!!!!!!!!!! ∵Δ＝ｂ２ －４ａｃ＝４２ －４×１×２＝８＞０． （３分）!!!!! ∴方程有两个不等的实数根， ｘ＝－ｂ± ｂ２ －４槡 ａｃ ２ａ （４分）!!!!!!!!!!!! ＝ 槡－４± ８ ２×１ 槡＝－２± ２， （６分）!!!!!!!!!!!!!!! 即 ｘ１ 槡＝－２＋ ２，ｘ２ 槡＝－２－ ２． （８分）!!!!!!!! １８．解：①当 ｍ＝０时，函数 ｙ＝ｘ是一次函数，与 ｘ轴只有一个 公共点． （１分）!!!!!!!!!!!!!!!!! ②当 ｍ≠０时，函数 ｙ＝ｍｘ２ ＋（２ｍ＋１）ｘ＋ｍ是二次函数． ∵函数图象与 ｘ轴只有一个公共点， ∴关于 ｘ的方程 ｍｘ２ ＋（２ｍ＋１）ｘ＋ｍ＝０有两个相等的实 数根． ∴Δ＝０． （３分）!!!!!!!!!!!!!!!!! 又∵Δ＝（２ｍ＋１）２ －４ｍ·ｍ （４分）!!!!!!!! ＝４ｍ２ ＋４ｍ＋１－４ｍ２ ＝４ｍ＋１． （６分）!!!!!!!!!!!!! ∴４ｍ＋１＝０， （７分）!!!!!!!!!!!!!!! 解得 ｍ＝－１ ４． （８分）!!!!!!!!!!!!!! 综上所述，当 ｍ＝０或 －１ ４时，函数图象与 ｘ轴只有一个 公共点． １９．解：（１）方法一（列表法）：根据题意，可以列出如下表格： 　　　小武（ｘ） 小明（ｙ）　　　 １ ２ ３ ４ １ （１，１） （２，１） （３，１） （４，１） ２ （１，２） （２，２） （３，２） （４，２） ３ （１，３） （２，３） （３，３） （４，３） ４ （１，４） （２，４） （３，４） （４，４） （４分）!!!!!!!!!!!!!!!!!!!!! 方法二（画 树 状 图 法）：根 据 题 意，可 以 画 出 如 下 的 树 状图： 第 １９题解图 由列表（树状图）可得，可能出现的情况共有 １６种． （４分） !! !!!!!!!!!!!!!!!!!!! （２）由（１）知，所有可能出现的结果共有 １６种，且这些结 果出现的可能性相等． （５分）!!!!!!!!!!! 其中他们“心灵相通”的结果有 ４种． （６分）!!!!! ∴Ｐ（心灵相通）＝４ １６＝１ ４． （７分）!!!!!!!!! ∴他们“心灵相通”的概率是 １ ４． （８分）!!!!!!! ２０．证明：如解图，连接 ＯＣ， （１分）!!!!!!!!!!! 　第 ２０题解图 ∵ＯＡ＝ＯＢ，ＣＡ＝ＣＢ， （３分）!!!!!!!!!!!! ∴ＯＣ⊥ＡＢ． （６分）!!!!!!!!!!!!!!!! 又∵ＡＢ经过⊙Ｏ半径的外端点 Ｃ， （７分）!!!!!! ∴直线 ＡＢ是⊙Ｏ的切线． （８分）!!!!!!!!! ２１．解：（１）作图如解图①， 第 ２１题解图① （２分）!!!!!!!!!!!!!!!!!!!!! 则△ＡＤＥ为所画的三角形． （３分）!!!!!!!!! （２）如解图②，延长 ＥＤ，ＢＣ交于点 Ｆ． 第 ２１题解图②                                                                    １ ∵△ＡＢＣ绕点 Ａ旋转得到△ＡＤＥ， ∴△ＡＢＣ≌△ＡＤＥ． （４分）!!!!!!!!!!!! ∴∠ＡＣＢ＝∠ＡＥＤ，∠ＣＡＥ＝１２０°． （５分）!!!!!! ∵∠ＡＣＢ＋∠ＡＣＦ＝１８０°， ∴∠ＡＥＦ＋∠ＡＣＦ＝１８０°． （６分）!!!!!!!!!! 在四边形 ＡＣＦＥ中， ∠ＡＥＦ＋∠ＣＦＥ＋∠ＡＣＦ＋∠ＣＡＥ＝３６０°， ∴∠ＣＡＥ＋∠ＣＦＥ＝１８０°． （７分）!!!!!!!!!! ∴∠ＣＦＥ＝６０°． ∴直线 ＢＣ与直线 ＤＥ相交所成的锐角是 ６０°．（８分） ２２．解：（１）答案不唯一：△ＣＥＦ∽△ＤＨＦ，△ＡＨＧ∽△ＣＥＧ， △ＡＢＣ∽△ＡＤＣ； （４分）!!!!!!!!!!!!! （２）如解图，连接 ＡＥ． 第 ２２题解图 ∵四边形 ＡＢＣＤ是正方形， ∴ＡＢ＝ＡＤ，∠ＡＢＥ＝∠ＡＤＣ＝∠ＢＣＤ ＝∠ＢＡＤ＝９０°． ∴∠ＡＤＦ＝９０°＝∠ＡＢＥ． （５分）! ∵ＤＦ＝ＢＥ， ∴△ＡＢＥ≌△ＡＤＦ， ∴ＡＥ＝ＡＦ，∠ＢＡＥ＝∠ＤＡＦ， （７分） !!! !!!!!!!!!! ∴∠ＥＡＦ＝∠ＥＡＤ＋∠ＤＡＦ＝∠ＥＡＤ＋∠ＢＡＥ＝∠ＢＡＤ ＝９０°． ∴∠ＡＦＥ＝４５°． （８分）!!!!!!!!!!!!!! ∵ＡＣ是对角线， ∴∠ＡＣＤ＝４５°＝∠ＡＦＥ． ∴△ＡＦＧ∽△ＡＣＦ． （９分）!!!!!!!!!!!!! ∴ＡＦ ＡＣ＝ＡＧ ＡＦ． ∴ＡＦ２ ＝ＡＧ·ＡＣ． （１０分）!!!!!!!!!!!!! ２３．解：（１）将点 Ａ（６，ｍ）代入 ｙ＝１ ３ｘ， 得 ｍ＝１ ３ ×６＝２， （１分）!!!!!!!!!!!!! ∴Ａ（６，２）． （２分）!!!!!!!!!!!!!!!! 将点 Ａ（６，２）代入 ｙ＝ｋ ｘ，得 ２＝ｋ ６， 解得 ｋ＝１２． （４分）!!!!!!!!!!!!!!! （２）解法一：如解图①，过点 Ａ作关于直线 ｙ＝ｘ的对称点 Ｂ，过点 Ａ作 ＡＣ⊥ｘ轴于点 Ｃ，交直线 ｙ＝ｘ于点 Ｄ，连接 ＯＢ，ＡＢ，过点 Ｂ作 ＢＥ⊥ｙ轴于点 Ｅ， 第 ２３题解图① ∴∠ＡＣＯ＝∠ＢＥＯ＝９０°． ∵Ａ（６，２）， ∴Ｃ（６，０），ＡＣ＝２，ＯＣ＝６． 将 ｘ＝６代入 ｙ＝ｘ，得 ｙ＝６， ∴Ｄ（６，６）． ∴ＯＣ＝ＤＣ＝６． ∴∠ＣＯＤ＝４５°． （５分）!!!!!!!!!!!!!! ∵∠ＣＯＥ＝９０°， ∴∠ＥＯＤ＝∠ＣＯＤ＝４５°． ∵点 Ａ，Ｂ关于直线 ｙ＝ｘ对称， ∴ＯＤ垂直平分 ＡＢ． ∴∠ＢＯＤ＝∠ＡＯＤ． ∴∠ＥＯＢ＝∠ＣＯＡ，∠ＢＥＯ＝∠ＡＣＯ＝９０°． （６分）!!! ∴ＯＢ＝ＯＡ． ∴△ＯＡＣ≌△ＯＢＥ（ＡＡＳ）． （７分）!!!!!!!!! ∴ＢＥ＝ＡＣ＝２，ＯＥ＝ＯＣ＝６． ∴Ｂ（２，６）． （８分）!!!!!!!!!!!!!!!! ∵２×６＝１２＝ｋ， （９分）!!!!!!!!!!!!!! ∴点 Ｂ在双曲线 ｙ＝１２ ｘ上． （１０分）!!!!!!!!! 解法二：如解图②，过点 Ａ作关于直线 ｙ＝ｘ的对称点 Ｂ， 过点 Ａ作 ＡＣ⊥ｘ轴于点 Ｃ，交直线 ｙ＝ｘ于点 Ｄ， 连接 ＤＢ并延长交 ｙ轴于点 Ｅ，连接 ＡＢ， 第 ２３题解图② ∴∠ＡＣＯ＝９０°． ∵Ａ（６，２）， ∴Ｃ（６，０），ＡＣ＝２． 将 ｘ＝６代入 ｙ＝ｘ，得 ｙ＝６， ∴Ｄ（６，６）． ∴ＯＣ＝ＤＣ＝６． ∴ＤＡ＝ＤＣ－ＡＣ＝４，∠ＣＤＯ＝４５°． （５分）!!!!!! ∵点 Ａ，Ｂ关于直线 ｙ＝ｘ对称， ∴ＯＤ垂直平分 ＡＢ． ∴ＤＢ＝ＤＡ＝４． ∴∠ＢＤＯ＝∠ＡＤＯ＝４５°． （６分）!!!!!!!!!! ∴∠ＡＤＢ＝９０°． ∵∠ＯＣＤ＝∠ＣＯＥ＝９０°， ∴四边形 ＣＯＥＤ是矩形． （７分）!!!!!!!!!! ∴∠ＢＥＯ＝９０°，ＯＥ＝ＣＤ＝６，ＥＤ＝ＯＣ＝６． ∴ＢＥ⊥ｘ轴，ＢＥ＝ＥＤ－ＤＢ＝２． ∴Ｂ（２，６）． （８分）!!!!!!!!!!!!!!!! 由（１）得双曲线的解析式是 ｙ＝１２ ｘ， 把 ｘ＝２代入，得 ｙ＝１２ ２ ＝６， （９分）!!!!!!!!! ∴点 Ｂ在双曲线 ｙ＝１２ ｘ上． （１０分）!!!!!!!!! ２４．（１）证明：∵ＢＣ＝ＢＣ， ∴∠ＢＡＣ＝∠ＢＥＣ． （１分）!!!!!!!!!!!! ∵ＢＦ⊥ＡＣ于点 Ｆ，ＣＥ⊥ＡＢ于点 Ｄ， ∴∠ＢＦＡ＝∠ＢＤＧ＝∠ＢＤＥ＝９０°． （２分）!!!!!! ∴∠ＡＢＦ＝∠ＡＢＥ． （３分）!!!!!!!!!!!!! ∴∠ＢＧＤ＝∠ＢＥＣ．（等角的余角相等） （４分）!!!! ∴ＢＥ＝ＢＧ． （５分）!!!!!!!!!!!!!!!! （２）解：如解图，连接 ＯＢ，ＯＥ，ＡＥ，ＣＨ． 第 ２４题解图 ∵ＢＨ⊥ＡＢ， ∴∠ＡＢＨ＝∠ＢＤＥ＝９０°． ∴ＢＨ∥ＣＤ． （６分）!!!!!!! ∵四边形 ＡＢＨＣ内接于⊙Ｏ， ∴∠ＡＣＨ＋∠ＡＢＨ＝１８０°． ∴∠ＡＣＨ＝９０°＝∠ＡＦＢ． ∴ＢＦ∥ＣＨ． ∴四边形 ＢＧＣＨ是平行四边形． （７分） ! !!!!!!!!!! ∴ＣＧ＝ＢＨ＝４． ∵ＢＥ＝ＯＢ＝ＯＥ， ∴△ＯＢＥ是等边三角形． ∴∠ＢＯＥ＝６０°． （８分）!!!!!!!!!!!!!! ∵ＢＥ＝ＢＥ， ∴∠ＢＡＥ＝１ ２∠ＢＯＥ＝３０°． ∵∠ＡＤＥ＝９０°                                                                        ， ２ ∴ＤＥ＝１ ２ＡＥ． （９分）!!!!!!!!!!!!!! 设 ＤＥ＝ｘ，则 ＡＥ＝２ｘ， ∵由（１）得，ＢＥ＝ＢＧ，ＡＢ⊥ＣＤ， ∴ＤＧ＝ＤＥ＝ｘ． ∴ＣＤ＝ｘ＋４． 在 Ｒｔ△ＡＤＥ中，ＡＤ＝ ＡＥ２ －ＤＥ槡 ２ 槡＝ ３ｘ． （１０分）!!! 在 Ｒｔ△ＡＤＣ中，ＡＤ２ ＋ＣＤ２ ＝ＡＣ２， 即（槡３ｘ）２ ＋（ｘ＋４）２ ＝（ 槡２ ７）２， 解得 ｘ１ ＝１，ｘ２ ＝－３＜０（舍去）， ∴ＤＧ＝ＤＥ＝１． （１１分）!!!!!!!!!!!!!! ∴ＣＥ＝ＣＧ＋ＧＤ＋ＤＥ＝６． （１２分）!!!!!!!!! ２５．解：（１）依题意，得 －ｂ ２ａ＝０， ａ＋ｂ＋ｃ＝２， ４ａ＋２ｂ＋ｃ＝５{ ， 解得 ａ＝１， ｂ＝０， ｃ＝１{ ． （３分）!!!!!!!!!!!!!!! ∴二次函数的解析式为 ｙ＝ｘ２ ＋１． （４分）!!!!!! （２）设过点 Ｅ（０，２）的一次函数的解析式为 ｙ＝ｋｘ＋ｍ（ｋ ≠０）， 则 ２＝ｋ·０＋ｍ， ∴ｍ＝２． 即该一次函数的解析式为 ｙ＝ｋｘ＋２（ｋ≠０）． （５分）!! 设 Ａ（ｘ１，ｙ１），Ｂ（ｘ２，ｙ２）（ｘ１ ＜ｘ２），则 Ｃ（ｘ１，０），Ｄ（ｘ２，０）． 将 ｙ＝ｋｘ＋２代入 ｙ＝ｘ２ ＋１，得 ｋｘ＋２＝ｘ２ ＋１， 则 ｘ２ －ｋｘ－１＝０， 解得 ｘ＝ｋ± ｋ２槡 ＋４ ２ ， ∴ｘ１ ＝ｋ－ ｋ２槡 ＋４ ２ ，ｘ２ ＝ｋ＋ ｋ２槡 ＋４ ２ ． ①依题意， 得 ＣＤ＝ｘ２ －ｘ１ ＝ｋ＋ ｋ２槡 ＋４ ２ －ｋ－ ｋ２槡 ＋４ ２ ＝ ｋ２槡 ＋４， （６分）!!!!!!!!!!!!!!!!!!! ∵ＣＤ＝３， ∴ｋ２ ＋４＝９， 解得 ｋ 槡＝± ５， （７分）!!!!!!!!!!!!!! ∴该一次函数的解析式是 ｙ 槡＝ ５ｘ＋２或 ｙ 槡＝－ ５ｘ＋２． （９分）!!!!!!!!!!!!!!!!!!! ②依题意，得 Ｓ１ ＝１ ２ＡＣ·ＯＣ＝１ ２ｙ１·｜ｘ１｜＝－１ ２ｘ１ｙ１， （１０分）!!!!!!!!!!!!!!!!!!! Ｓ２ ＝１ ２ＣＤ·ＯＥ＝１ ２（ｘ２ －ｘ１）·２＝ｘ２ －ｘ１， Ｓ３ ＝１ ２ＢＤ·ＯＤ＝１ ２ｘ２ｙ２， （１１分）!!!!!!!!! ∴Ｓ２ ２ ＝（ｘ２ －ｘ１）２ ＝ｋ２ ＋４． Ｓ１Ｓ３ ＝－１ ２ｘ１ｙ１· １ ２ｘ２ｙ２ ＝－１ ４ｘ１ｘ２（ｋｘ１ ＋２）（ｋｘ２ ＋２） ＝－１ ４ｘ１ｘ２［ｋ２ｘ１ｘ２ ＋２ｋ（ｘ１ ＋ｘ２）＋４］． （１２分）!! ∵ｘ１ ＝ｋ－ ｋ２槡 ＋４ ２ ，ｘ２ ＝ｋ＋ ｋ２槡 ＋４ ２ ， ∴ｘ１ ＋ｘ２ ＝ｋ，ｘ１ｘ２ ＝－１． ∴Ｓ１Ｓ３ ＝－１ ４ ×（－１）×［ｋ２ ×（－１）＋２ｋ·ｋ＋４］ ＝１ ４（ｋ２ ＋４）． （１３分）!!!!!!!!!!! ∴Ｓ２ ２ ＝４Ｓ１Ｓ３． 故存在实数 ｔ＝４，使得 Ｓ２ ２ ＝ｔＳ１Ｓ３ 成立． （１４分）                                          !!!! ３ ２０１８－２０１９学年（上）厦门市九年级质量检测 数学参考答案 说明：解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照评分量表的要求相应评分． 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分） １．Ａ　２．Ｃ　３．Ｄ　４．Ｂ　５．Ｃ　６．Ｄ　７．Ａ　８．Ｂ　９．Ｄ　 １０．Ｃ 二、填空题（本大题共 ６小题，每题 ４分，共 ２４分） １１．１ ２　１２．－１　１３．１ １４．直角三角形是完全三角形；如：等腰直角三角形，或三边分 别为 ５，１２，１３的三角形，或三边比为 ５：１２：１３的三角形等． １５．槡１０ ２ 　１６．ｂ＞３ 三、解答题（本大题有 ９小题，共 ８６分） １７．解：ａ＝１，ｂ＝－３，ｃ＝１． Δ＝ｂ２ －４ａｃ ＝５＞０． ４分!!!!!!!!!!!!!!!!! ∴方程有两个不相等的实数根． ｘ＝－ｂ± ｂ２ －４槡 ａｃ ２ａ ＝ 槡３± ５ ２ ． ６分!!!!!!!!!!!!!!!!! ｘ１ ＝ 槡３＋ ５ ２ ，ｘ２ ＝ 槡３－ ５ ２ ． ８分!!!!!!!!!!!! １８．解：（１－ ２ ｘ＋１）÷ｘ２ －１ ２ｘ＋２ ＝（ｘ＋１－２ ｘ＋１ ）·２ｘ＋２ ｘ２ －１ ２分!!!!!!!!!!! ＝ｘ－１ ｘ＋１· ２（ｘ＋１） （ｘ＋１）（ｘ－１） ５分!!!!!!!!!! ＝ ２ ｘ＋１． ６分!!!!!!!!!!!!!!!!! 当 ｘ 槡＝ ２－１时，原式 ＝２ 槡２ 槡＝ ２． ８分!!!!!!!! １９．解：∵当 ｘ＝２时，ｙ＝２． ∴（２－１）２ ＋ｎ＝２． 解得 ｎ＝１． ∴二次函数的解析式为：ｙ＝（ｘ－１）２ ＋１． ４分!!!! 列表得： ｘ … －１ ０ １ ２ ３ … ｙ … ５ ２ １ ２ ５ … 函数图象如解图： 第 １９题解图 ８分!!!!!!!!!!!! ２０．解：（１）如解图①，点 Ｅ即为所求． ３分!!!!!!!! （２）解法一：连接 ＥＢ，ＥＣ， 由（１）得，ＥＢ＝ＥＣ． 第 ２０题解图① ∵四边形 ＡＢＣＤ是矩形， ∴∠Ａ＝∠Ｄ＝９０°，ＡＢ＝ＤＣ． ∴△ＡＢＥ≌△ＤＣＥ． ６分!!!!!!! ∴ＡＥ＝ＥＤ＝１ ２ＡＤ＝３． ７分!!!!! 在 Ｒｔ△ＡＢＥ中，ＥＢ＝ ＡＢ２ ＋ＡＥ槡 ２． ∴ＥＢ＝５． ８分!!!!!!!!!!! 解法二： 如解图②，设线段 ＢＣ的中垂线 ｌ交 ＢＣ 于点 Ｆ， ∴∠ＢＦＥ＝９０°，ＢＦ＝１ ２ＢＣ． ∵四边形 ＡＢＣＤ是矩形， ∴∠Ａ＝∠ＡＢＦ＝９０°，ＡＤ＝ＢＣ． 第 ２０题解图② 在四边形 ＡＢＦＥ中，∠Ａ＝∠ＡＢＦ＝∠ＢＦＥ ＝９０°， ∴四边形 ＡＢＦＥ是矩形． ６分!!!! ∴ＥＦ＝ＡＢ＝４． ７分!!!!!!!! 在 Ｒｔ△ＢＦＥ中，ＥＢ＝ ＥＦ２ ＋ＢＦ槡 ２． ∴ＥＢ＝５． ８分!!!!!!!!!!! ２１．证明：如解图，连接 ＯＤ， ∵ＡＢ是⊙Ｏ直径且 ＡＢ＝４， ∴ｒ＝２． 设∠ＡＯＤ＝ｎ°， 第 ２０题解图 ∵ ) ＡＤ的长为４π ３， ∴ｎπｒ １８０＝４π ３． 解得 ｎ＝１２０． 即∠ＡＯＤ＝１２０°． ３分!!!!!!! 在⊙Ｏ中，ＤＯ＝ＡＯ， ∴∠Ａ＝∠ＡＤＯ． ∴∠Ａ＝１ ２（１８０°－∠ＡＯＤ）＝３０°． ５分!!!!!!! ∵∠Ｃ＝６０°， ∴∠ＡＢＣ＝１８０°－∠Ａ－∠Ｃ＝９０°． ６分!!!!!!! 即 ＡＢ⊥ＢＣ． ７分!!!!!!!!!!!!!!!!! 又∵ＡＢ为直径， ∴ＢＣ是⊙Ｏ的切线． ８分!!!!!!!!!!!!! 第 ２２题解图① ２２．解：（１）解法一： 如解图 ①，过点 Ｐ作 ＰＦ⊥ ｙ轴 于 Ｆ， ∵点 Ｐ到边 ＡＤ的距离为 ｍ． ∴ＰＦ＝ｍ＝１ ４． 的横坐标为 １ ４． 由题得，Ｃ（１，１），可得直线 ＡＣ的解析式为：ｙ＝ｘ． ３分 !!! !!!!!!!!!!!!!!!!!!!! 当 ｘ＝１ ４时，ｙ＝１ ４． ４分                                                                  !!!!!!!!!!!!! ４ 所以 Ｐ（１ ４，１ ４）． ５分!!!!!!!!!!!!!! 解法二： 如解图①，过点 Ｐ作 ＰＥ⊥ｘ轴于 Ｅ，作 ＰＦ⊥ｙ轴于 Ｆ， ∵ＰＥ＝ｎ，ＰＦ＝ｍ． ∴Ｐ（ｍ，ｎ）． １分!!!!!!!!!!!!!!!!! ∵四边形 ＡＢＣＤ是正方形， ∴ＡＣ平分∠ＤＡＢ． ２分!!!!!!!!!!!!!! ∵点 Ｐ在对角线 ＡＣ上， ∴ｍ＝ｎ＝１ ４． ∴Ｐ（１ ４，１ ４）． ５分!!!!!!!!!!!!!!!! 第 ２２题解图② （２）解法一：如解图②，以 Ａ为原 点，以边 ＡＢ所在直线为 ｘ轴，建 立平面直角坐标系． 则由（１）得 Ｐ（ｍ，ｎ）． 若点 Ｐ在△ＤＡＢ的内部， 点 Ｐ需满足的条件是： ①在 ｘ轴上方，且在直线 ＢＤ的 下方； ②在 ｙ轴右侧，且在直线 ＢＤ的左侧． 由①，设直线 ＢＤ的解析式为：ｙ＝ｋｘ＋ｂ， 把点 Ｂ（１，０），Ｄ（０，１）分别代入， 可得直线 ＢＤ的解析式为：ｙ＝－ｘ＋１． ６分!!!!!! 当 ｘ＝ｍ时，ｙ＝－ｍ＋１． 由点 Ｐ在直线 ＢＤ的下方，可得 ｎ＜－ｍ＋１． ７分!!! 由点 Ｐ在 ｘ轴上方，可得 ｎ＞０ ８分!!!!!!!!! 即 ０＜ｎ＜－ｍ＋１． 同理，由②可得 ０＜ｍ＜－ｎ＋１． ９分!!!!!!!! 所以 ｍ，ｎ需满足的条件是：０＜ｎ＜－ｍ＋１且 ０＜ｍ＜－ｎ ＋１． １０分!!!!!!!!!!!!!!!!!!! 第 ２２题解图③ 解法二：如解图③，过点 Ｐ作 ＰＥ⊥ＡＢ 于 Ｅ，作 ＰＦ⊥ＡＤ于 Ｆ， ∵点 Ｐ到 边 ＡＤ，ＡＢ的 距 离 分 别 为 ｍ，ｎ， ∴ＰＥ＝ｎ，ＰＦ＝ｍ． 在正 方 形 ＡＢＣＤ 中，∠Ａ＝∠ＰＥＡ＝ ∠ＰＦＡ＝９０°． ∴四边形 ＰＥＡＦ为矩形． ∴ＰＥ＝ＦＡ＝ｎ． 若点 Ｐ在△ＤＡＢ的内部， 则延长 ＦＰ交对角线 ＢＤ于点 Ｍ． 在 Ｒｔ△ＤＦＭ中，∠ＤＭＦ＝９０°－∠ＦＤＭ＝４５°． ∴∠ＤＭＦ＝∠ＦＤＭ． ∴ＤＦ＝ＦＭ． ∵ＰＦ＜ＦＭ， ∴ＰＦ＜ＤＦ ７分!!!!!!!!!!!!!!!!! ∴ＰＥ＋ＰＦ＝ＦＡ＋ＰＦ＜ＦＡ＋ＤＦ． 即 ｍ＋ｎ＜１． 又∵ｍ＞０，ｎ＞０， ∴ｍ，ｎ需满足的条件是 ｍ＋ｎ＜１且 ｍ＞０且 ｎ＞０． １０分 !! !!!!!!!!!!!!!!!!!!!! ２３．解：（１）估计运到的 ２０００公斤鱼中活鱼的总重量为 １７６０ 公斤． ２分!!!!!!!!!!!!!!!!!!! （２）①根据表二的销售记录可知，活鱼的售价每增加 １ 元，其日销售量就减少 ４０公斤，所以按此变化规律可以估 计当活鱼的售价定为 ５２．５元／公斤时，日销售量为 ３００公 斤． ５分!!!!!!!!!!!!!!!!!!!! ②解法一：由（２）①，若活鱼售价在 ５０元／公斤的基础上，售 价增加 ｘ元／公斤，则可估计日销售量在 ４００公斤的基础上 减少 ４０ｘ公斤， 设批发店每日卖鱼的最大利润为 ｗ，由题得 ｗ＝（５０＋ｘ－２０００×４４ １７６０ ）（４００－４０ｘ） ＝－４０ｘ２ ＋４００ｘ ＝－４０（ｘ－５）２ ＋１０００． ７分!!!!!!!!!!! 由“在 ８天内卖完这批活鱼”，可得 ８（４００－４０ｘ）≤１７６０，解 ｘ≤４．５． 根据实际意义，有 ４００－４０ｘ≥０，解得 ｘ≤１０． 所以 ｘ≤４．５． ９分!!!!!!!!!!!!!!!! 因为 －４０＜０， 所以当 ｘ＜５时，ｗ随 ｘ的增大而增大， 所以售价定为 ５４．５元／公斤，每日卖鱼可能达到的最大利 润为 ９９０元． １０分!!!!!!!!!!!!!!!! 解法二：设这 ８天活鱼的售价为 ｘ元／公斤，日销售量为 ｙ 公斤，根据活鱼的售价与日销售量之间的变化规律，不妨 设 ｙ＝ｋｘ＋ｂ． 由表二可知，当 ｘ＝５０时，ｙ＝４００；当 ｘ＝５１时，ｙ＝３６０， 所以 ５０ｋ＋ｂ＝４００ ５１ｋ＋ｂ{ ＝３６０， 解得 ｋ＝－４０ ｂ{ ＝２４００， 可得 ｙ＝－４０ｘ＋２４００． 设批发店每日卖鱼的最大利润为 ｗ，由题得 ｗ＝（ｘ－２０００×４４ １７６０ ）（２４００－４０ｘ） ７分!!!!!!!! ＝－４０ｘ２ ＋４４００ｘ－１２００００ ＝－４０（ｘ－５５）２ ＋１０００． 由“在 ８天内卖完这批活鱼”，可得 ８（－４０ｘ＋２４００）≤ １７６０，解得 ｘ≤５４．５． 根据实际意义，有 －４０ｘ＋２４００≥０，解得 ｘ≤６０． 所以 ｘ≤５４．５． ９分!!!!!!!!!!!!!!!! 因为 －４０＜０， 所以当 ｘ＜５５时，ｗ随 ｘ的增大而增大， 所以售价定为 ５４．５元／公斤，每日卖鱼可能达到的最大利 第 ２４题解图① 润为 ９９０元． １０分!!!!!! ２４．（１）解：如解图①，连接 ＡＢ． 在⊙Ｏ中， ∵∠ＡＰＱ＝∠ＢＰＱ＝４５°， ∴∠ＡＰＢ＝∠ＡＰＱ＋∠ＢＰＱ＝９０°． １分!!!!!!!!!!! ∴ＡＢ是⊙Ｏ的直径． ３分!!! ∴在 Ｒｔ△ＡＰＢ中，ＡＢ＝ ＡＰ２ ＋ＢＰ槡 ２． ∴ＡＢ＝３． ５分!!!!!!!!!!!!!!!!!! 第 ２４题解图② ∴⊙Ｏ的半径是 ３ ２． ６分!!!! （２）解：ＡＢ∥ＯＮ． 证明：如解图②，连接 ＯＡ，ＯＢ，ＯＱ， Ｃ为 ＡＢ，Ｃ为交点， 在⊙Ｏ中                                                                        ， ５ ∵ ) ＡＱ＝ ) ＡＱ， ) ＢＱ＝ ) ＢＱ， ∴∠ＡＯＱ＝２∠ＡＰＱ，∠ＢＯＱ＝２∠ＢＰＱ． 又∵∠ＡＰＱ＝∠ＢＰＱ，∴∠ＡＯＱ＝∠ＢＯＱ． ７分!!!! 在△ＡＯＢ中，ＯＡ＝ＯＢ，∠ＡＯＱ＝∠ＢＯＱ， ∴ＯＣ⊥ＡＢ，即∠ＯＣＡ＝９０°． ８分!!!!!!!!!! 在⊙Ｏ中，ＯＰ＝ＯＱ． ∴∠ＯＰＮ＝∠ＯＱＰ． 延长 ＰＯ交⊙Ｏ于点 Ｒ，则有 ２∠ＯＰＮ＝∠ＱＯＲ． ∵∠ＮＯＰ＋２∠ＯＰＮ＝９０°． １１分!!!!!!!!!! ∴∠ＮＯＱ＋∠ＯＣＡ＝１８０°． ∴ＡＢ∥ＯＮ． １２分!!!!!!!!!!!!!!!! ２５．解：（１）①如解图①即为所求； ３分!!!!!!!!! 第 ２５题解图① ②由①可求得，直线 ｌ：ｙ＝ １ ２ｘ＋２，抛物线 ｍ：ｙ＝－１ ４ ｘ２ ＋２， ５分!!!!!! 因为点 Ｑ在抛物线 ｍ上，过 点 Ｑ且与 ｘ轴垂直的直线 与 ｌ交于点 Ｈ， 所以可设点 Ｑ的坐标为（ｅ， －１ ４ｅ２ ＋２），点 Ｈ的坐标为 （ｅ，１ ２ｅ＋２），其中（－２≤ｅ≤０）． 当 －２≤ｅ≤０时，点 Ｑ总在点 Ｈ的正上方，可得 ｄ＝－１ ４ｅ２ ＋２－（１ ２ｅ＋２） ６分!!!!!!!!!! 第 ２５题解图② ＝－１ ４ｅ２ －１ ２ｅ ＝－１ ４（ｅ＋１）２ ＋１ ４． 因为 －１ ４ ＜０， 所以当 ｄ随 ｅ的增大而增大 时，ｅ的取值范围是 －２≤ｅ ≤ －１． ７分!!!!!! （２）解法一： 因为 Ｂ（ｐ，ｑ），Ｃ（ｐ＋４，ｑ）在抛物线 ｍ上， 所以抛物线 ｍ的对称轴为 ｘ＝ｐ＋２． 又因为抛物线 ｍ与 ｘ轴只有一个交点， 可设抛物线的解析式为 ｙ＝ａ（ｘ－ｐ－２）２． 当 ｘ＝０时，ｙＦ ＝ａ（ｐ＋２）２． 可得 Ｆ（０，ａ（ｐ＋２）２）． ９分!!!!!!!!!!!! 把 Ｂ（ｐ，ｑ）代入 ｙ＝ａ（ｘ－ｐ－２）２，可得 ｑ＝ａ（ｐ－ｐ－２）２． 化简可得 ｑ＝４ａ①． 设直线 ｌ的解析式为 ｙ＝ｋｘ＋２， 分别把 Ｂ（ｐ，ｑ），Ｎ（ｐ＋２，０）代入 ｙ＝ｋｘ＋２，可得 ｑ＝ｋｐ＋２ ②，及 ０＝ｋ（ｐ＋２）＋２③． 由①，②，③可得 ａ＝ １ ２＋ｐ， 所以 Ｆ（０，ｐ＋２）． 又因为 Ｎ（ｐ＋２，０）， １３分!!!!!!!!!!!!! 所以 ＯＮ＝ＯＦ，且∠ＮＯＦ＝９０°． 所以△ＮＯＦ为等腰直角三角形． １４分!!!!!!!! 解法二： 因为直线过点 Ａ（０，２）， 不妨设直线 ｌ：ｙ＝ｋｘ＋２， 因为 Ｂ（ｐ，ｑ），Ｃ（ｐ＋４，ｑ）在抛物线 ｍ上， 所以抛物线 ｍ的对称轴为 ｘ＝ｐ＋２． 又因为抛物线的顶点 Ｎ在直线 ｌ：ｙ＝ｋｘ＋２上， 可得 Ｎ（ｐ＋２，ｋ（ｐ＋２）＋２）． 所以抛物线 ｍ：ｙ＝ａ（ｘ－ｐ－２）２ ＋ｋ（ｐ＋２）＋２． 当 ｘ＝０时，ｙ＝ａ（ｐ＋２）２ ＋ｋ（ｐ＋２）＋２． 即点 Ｆ的坐标是（０，ａ（ｐ＋２）２ ＋ｋ（ｐ＋２）＋２）． ９分!! 因为直线 ｌ，抛物线 ｍ经过点 Ｂ（ｐ，ｑ），可得 ｋｐ＋２＝ｑ ４ａ＋ｋ（ｐ＋２）＋２＝{ ｑ， 可得 ｋ＝－２ａ． 因为抛物线 ｍ与 ｘ轴有唯一交点， 可知关于 ｘ的方程 ｋｘ＋２＝ａ（ｘ－ｐ－２）２ ＋ｋ（ｐ＋２）＋２ 中，Δ＝０． 结合 ｋ＝－２ａ，可得 ｋ（ｐ＋２）＝－２． 可得 Ｎ（ｐ＋２，０），Ｆ（０，ｐ＋２）． １３分!!!!!!!!! 所以 ＯＮ＝ＯＦ，且∠ＮＯＦ＝９０°． 所以△ＮＯＦ是等腰直角三角形． １４分                                                                        !!!!!!!! ６ 泉州市 ２０１８－２０１９学年度上学期初三教学质量检测 数学参考答案及评分标准 一、选择题（每小题 ４分，共 ４０分） １．Ｄ　２．Ａ　３．Ｂ　４．Ｂ　５．Ｄ　６．Ｄ　７．Ｄ　８．Ｂ　 ９．Ｃ　１０．Ａ 二、填空题（每小题 ４分，共 ２４分） １１．１８　１２．ｘ１ ＝０，ｘ２ ＝３　１３．３ ５　１４．１０ ３　１５．６０ １７　 １６．ｂ或 ａ２ ｂ 三、解答题（共 ８６分） １７．解：原式 槡 槡 槡＝２ ３－ ３＋ ３ ６分!!!!!!!!!!!! 槡＝２ ３． ８分!!!!!!!!!!!!!!! １８．解：设转盘 １中的两种红色扇形分别为红 １，红 ２． 方法一：画树状图如下： 第 １８题解图 ４分!!!!!!!!!!!!!!!!!!!!!! 由树状图可知，共有 ６种等可能结果，其中“配橙色”即 “一红一黄”的结果有 ３种． ∴Ｐ（“配橙色”）＝３ ６ ＝１ ２． ７分!!!!!!!!!! ∴游戏者获胜的概率为 １ ２． ８分!!!!!!!!!! 方法二：列表如下： 　转盘 ２ 转盘 １　 红 黄 红 １ （红 １，红） （红 １，黄） 红 ２ （红 ２，红） （红 ２，黄） 黄 （黄，红） （黄，黄） ４分!!!!!!!!!!!!!!!!!!!!!! 由列表可知，共有 ６种等可能结果，其中“配橙色”即“一 红一黄”的结果有 ３种． ∴Ｐ（“配橙色”）＝３ ６ ＝１ ２． ∴游戏者获胜的概率为 １ ２． ８分!!!!!!!!!! １９．解：（Ⅰ）如解图，△Ａ′Ｂ′Ｃ′为所画三角形； ５分!!!! 第 １９题解图 （Ⅱ）Ａ′（０，４），Ｂ′（－２，０），Ｃ′（４，－２） ８分!!!!!! ２０．解：由已知条件得：∠ＡＢＣ＝３０°， ∠ＢＡＣ＝６０°＋３０°＝９０° ２分!!!!!!!!!!!! 在 Ｒｔ△ＡＢＣ中， ｃｏｓ∠ＡＢＣ＝ＡＢ ＢＣ， ∴ＢＣ＝ ＡＢ ｃｏｓ∠ＡＢＣ＝ ＡＢ ｃｏｓ３０°＝６０ 槡３ ２ 槡＝４０ ３（米）． ７分!!! 答：这栋楼高 ＢＣ的长为 槡４０ ３米． ８分!!!!!!!! ２１．解：设第二个月钢铁产量的增长率为 ｘ，则第三个月的增 长率为 ２ｘ，依题意得： １分!!!!!!!!!!!!! １００（１＋ｘ）（１＋２ｘ）＝１３２， ４分!!!!!!!!!!! 整理得：ｘ２ ＋１．５ｘ－０．１６＝０， 解得：ｘ１ ＝０．１，ｘ２ ＝－１．６（不合题意，舍去） ７分!!! ∴ｘ＝０．１＝１０％， 答：第二个月的增长率为 １０％． ８分!!!!!!!!! ２２．作图如解图； １分!!!!!!!!!!!!!!!! 第 ２２题解图 已知：如解图，△ＡＢＣ∽△Ａ′Ｂ′Ｃ′，△ＡＢＣ和△Ａ′Ｂ′Ｃ′的相 似比为 ｋ，ＡＤ、Ａ′Ｄ′分别是△ＡＢＣ△Ａ′Ｂ′Ｃ′的高． ３分!! 求证：ＡＤ Ａ′Ｄ′＝ｋ ４分!!!!!!!!!!!!!!!! 证明：∵△ＡＢＣ∽△Ａ′Ｂ′Ｃ′， ∴∠Ｂ ＝∠Ｂ′， ６分!!!!!!!!!!!!!!! ∵ＡＤ、Ａ′Ｄ′分别是△ＡＢＣ和△Ａ′Ｂ′Ｃ′的高， ∴∠ＢＤＡ＝∠Ｂ′Ｄ′Ａ′＝９０°， ∴△ＡＢＤ∽△Ａ′Ｂ′Ｄ′， ９分!!!!!!!!!!!!! ∴ ＡＤ Ａ′Ｄ′＝ＡＢ Ａ′Ｂ′＝ｋ． １０分!!!!!!!!!!!!!! ２３．解：（Ⅰ）∵一元二次方程 ｘ２ ＋３ｘ＋ｋ－３＝０有两个实 数根， ∴Δ＝３２ －４×１×（ｋ－３）≥０，解得：ｋ≤２１ ４． ３分!!!! ∴当 ｋ≤２１ ４时，关于 ｘ的一元二次方程 ｘ２ ＋３ｘ＋ｋ－３＝０ 有两个实数根． ４分!!!!!!!!!!!!!!! （Ⅱ）∵ｘ１ 是关于 ｘ的一元二次方程 ｘ２ ＋３ｘ＋ｋ－３＝０ 的根， ∴ｘ２ １ ＋３ｘ１ ＋ｋ－３＝０，即 ｘ２ １ ＝－３ｘ１ －ｋ＋３， ５分!!!! ∵ｘ２ １ ＋２ｘ１ ＋ｘ２ ＋ｋ＝３， ∴ －３ｘ１ －ｋ＋３＋２ｘ１ ＋ｘ２ ＋ｋ＝３． ７分!!!!!!!! ∴ｘ１ ＝ｘ２． ８分!!!!!!!!!!!!!!!!!! ∴Δ＝３２ －４×１×（ｋ－３）＝０． ９分!!!!!!!!! 解得：ｋ＝２１ ４． １０分!!!!!!!!!!!!!!!! ２４．解：（Ⅰ）∵直线 ｙ＝３ ４ｘ＋ｂ经过点 Ａ（０，３）， ∴ｂ＝３． ∴直线 ＡＢ的解析式为 ｙ＝３ ４ｘ＋３． ３分                                                                    !!!!!!! ７ （Ⅱ）在 ｙ＝３ ４ｘ＋３中，令 ｙ＝０，则 ｘ＝－４， ∴Ｂ（－４，０） 由（Ⅰ）得：Ａ（０，３），ＯＡ＝３，在 Ｒｔ△ＯＡＢ中，由勾股定理 得：ＡＢ＝５． ∵ＡＱ ＡＢ＝４ ５，∴ＡＱ＝４ ５ＡＢ＝４ ５ ×５＝４． ４分!!!!! 第 ２４题解图① ①当点 Ｑ在 ｙ轴的左侧时，如 解图①， ∵ＰＱ⊥ＡＢ，ＯＢ⊥ＯＡ， ∴∠ＰＱＡ＝∠ＡＯＢ＝９０°， 又∠ＢＡＯ＝∠ＰＡＱ， ∴△ＰＡＱ∽△ＢＡＯ， ∴ＡＱ ＡＯ＝ＡＰ ＡＢ， ∴ ４ ３ ＝ＡＰ ５，解得：ＡＰ＝２０ ３， ∴ＯＰ＝２０ ３ －３＝１１ ３， ∴点 Ｐ的坐标为（０，－１１ ３）． ６分!!!!!!!!!! ②当点 Ｑ在 ｙ轴的右侧时， 同①可得：ＡＰ＝２０ ３， ∴ＯＰ＝２０ ３ ＋３＝２９ ３， 综上，点 Ｐ的坐标为（０，－１１ ３）或（０，２９ ３）． ８分!!!! 第 ２４题解图② （Ⅲ）解法一：如解图②，连接 ＱＥ、ＯＥ． 在 Ｒｔ△ＢＰＱ 中，ＥＱ 是 Ｒｔ△ ＢＰＱ斜边 ＢＰ边上的中线， ∴ＥＱ＝１ ２ＢＰ， 同理，ＥＯ＝１ ２ＢＰ， ∴ＥＱ＝ＥＯ，即△ＥＱＯ是等腰三角形． 又 ＥＦ是△ＥＱＯ的中线， ∴ＥＦ⊥ＯＱ． ９分!!!!!!!!!!!!!!!! ∴∠ＱＦＥ＝９０°， ∵ＯＱ∥ＢＰ， ∴∠ＧＥＰ＝∠ＱＦＥ＝９０°， 又∠ＢＰＱ＝∠ＧＰＥ， ∴∠ＢＰＱ∽△ＧＰＥ， １１分!!!!!!!!!!!!! ∴ＰＧ ＰＢ＝ＰＥ ＰＱ， ∴ＰＥ·ＰＢ＝ＰＧ·ＰＱ， ∵ＰＥ＝１ ２ＰＢ， 第 ２４题解图③ ∴ １ ２ＰＢ·ＰＢ＝ＰＧ·ＰＱ ∴ＰＢ２ ＝２ＰＧ·ＰＱ． １３分! 解 法 二：如 解 图 ③，连 接 ＱＥ、ＯＥ． 在 Ｒｔ△ＢＰＱ 中，ＥＱ 是 Ｒｔ△ ＢＰＱ斜边 ＢＰ边上的中线， ∴ＥＱ＝１ ２ＢＰ， 同理，ＥＯ＝１ ２ＢＰ． ∴ＥＱ＝ＥＯ，即△ＥＱＯ是等腰三角形． 又 ＥＦ是△ＥＱＯ的中线， ∴ＥＦ⊥ＯＱ． ９分!!!!!!!!!!!!!!!! ∴∠ＱＦＥ＝９０°， ∵ＯＱ∥ＢＰ， ∴∠ＧＥＰ＝∠ＱＦＥ＝９０°， ∴ＥＦ⊥ＢＰ． 延长 ＰＱ至点 Ｐ′，使得：Ｐ′Ｑ＝ＰＱ，连接 Ｐ′Ｂ、ＢＧ， ∵ＢＱ为 ＰＰ′的垂直平分线， ∴ＢＰ′＝ＢＰ， ∴∠ＢＰＰ′＝∠ＢＰ′Ｐ①， ∵Ｅ是 ＢＰ的中点，ＥＦ⊥ＢＰ， ∴ＧＥ为 ＢＰ的垂直平分线． ∴ＢＧ＝ＰＧ， ∴∠ＢＰＧ＝∠ＰＢＧ②， 由①②可得：∠ＢＰ′Ｐ ＝∠ＰＢＧ，又∠ＢＰＧ ＝∠Ｐ′ＰＢ， ∴△ＢＰＰ′∽△ＧＰＢ， １１分!!!!!!!!!!!!! ∴ＰＢ ＰＧ＝ＰＰ′ ＰＢ． 即 ＰＢ２ ＝ＰＧ·ＰＰ′， 又 ＰＰ′＝２ＰＱ， ∴ＰＢ２ ＝２ＰＧ·ＰＱ． １３分!!!!!!!!!!!!! ２５．解：（Ⅰ） 槡４ ２； ２分!!!!!!!!!!!!!!!! （Ⅱ）∵点 Ａ与点 Ａ′关于 ＰＱ对称， ∴△ＡＰＱ与△Ａ′ＰＱ关于 ＰＱ对称， ∴∠ＤＡＣ＝∠ＱＡ′Ｐ＝∠ＱＣＤ＝４５°，ＡＰ＝ＰＡ′， ∵∠ＱＡ′Ｄ ＝∠ＱＡ′Ｐ＋∠ＰＡ′Ｄ， ∠ＱＡ′Ｄ ＝∠ＱＣＤ＋∠Ａ′ＱＣ， ∴∠ＰＡ′Ｄ ＝∠Ａ′ＱＣ． ４分!!!!!!!!!!!!! ∵ＡＢ＝４，ＡＰ＝３ＰＤ，∴ＰＤ＝１，ＡＰ＝ＰＡ′＝３， 在 Ｒｔ△ＰＤＡ′中，由勾股定理得：Ａ′Ｄ 槡＝２ ２， ｔａｎ∠Ａ′ＱＣ＝ｔａｎ∠ＰＡ′Ｄ＝ １ 槡２ ２ ＝槡２ ４． ７分!!!!!!! （Ⅲ）如解图，过点 Ｑ作直线 ＭＮ⊥ＡＤ于点 Ｍ，交 ＢＣ于点 Ｎ，则 ＭＮ⊥ＢＣ． 第 ２５题解图∵ＡＰ∥ＣＴ， ∴△ＡＰＱ∽△ＣＴＱ， ∴ＡＰ ＣＴ＝ＱＭ ＱＮ， 设 ＱＭ＝ｈ，则 ＱＮ＝４－ｈ， ∴ ａ ＣＴ＝ ｈ ４－ｈ，∴ＣＴ＝ａ（４－ｈ） ｈ ， ∴Ｓ＝１ ２ａｈ＋１ ２·ａ（４－ｈ） ｈ ·（４－ｈ）， ９分!!!!!! ∴Ｓ＝１ ２ａｈ＋ａ（４－ｈ）２ ２ｈ ， 整理得：ａｈ２ －（４ａ＋Ｓ）ｈ＋８ａ＝０（）， ∵关于 ｈ的一元二次方程（）有实根，∴Δ≥０， １０分 !!!                                                                        !!!!!!!!!!!!!!!!!!!! ８ ∴Δ＝（４ａ＋Ｓ）２ －４·ａ·８ａ≥０， （４ａ＋Ｓ）２≥３２ａ２，又 ４ａ＋Ｓ＞０， ∴４ａ＋Ｓ≥ 槡４ ２ａ， ∴Ｓ≥（ 槡４ ２－４）ａ， 当 Ｓ＝（ 槡４ ２－４）ａ时，由方程（）可得 ｈ 槡＝２ ２满足题意， １２分!!!!!!!!!!!!!!!!!!!!! 故当 ｈ 槡＝２ ２时，△ＡＰＱ与△ＣＴＱ面积之和 Ｓ的最小值为 （ 槡４ ２－４）ａ． １３分       !!!!!!!!!!!!!!!! ９ ２０１８－２０１９学年漳州上学期教学质量抽测数学参考答案 一、选择题（共 １０小题，每小题 ４分，满分 ４０分） １．Ｃ　２．Ｄ　３．Ｃ　４．Ａ　５．Ｂ　６．Ｄ　７．Ａ　８．Ｂ　９．Ａ　 １０．Ｄ 二、填空题（共 ６小题，每小题 ４分，满分 ２４分） １１．３　１２． 槡４ ５　１３．４　１４．２０　１５．－３　１６．１ 三、解答题（共 ９小题，满分 ８６分） １７．解法一：∵ａ＝２，ｂ＝４，ｃ＝－１， ∴Δ＝ｂ２ －４ａｃ＝４２ －４×２×（－１）＝２４＞０． ∴ｘ＝ 槡－４± ２４ ４ ＝－１±槡６ ２． ∴ｘ１ ＝－１＋槡６ ２，ｘ２ ＝－１－槡６ ２． 解法二：ｘ２ ＋２ｘ＝１ ２， ∴ｘ２ ＋２ｘ＋１＝１ ２ ＋１． ∴（ｘ＋１）２ ＝３ ２． ∴ｘ＋１＝±槡６ ２． ∴ｘ１ ＝－１＋槡６ ２，ｘ２ ＝－１－槡６ ２． １８．解法一：∵四边形 ＡＢＣＤ是正方形， ∴ＡＤ∥ＢＥ，∠ＡＣＢ＝４５°． ∵ＡＣ＝ＥＣ， ∴∠ＣＡＥ＝∠Ｅ＝２２．５°． ∵ＡＤ∥ＢＥ， ∴∠ＤＡＦ＝∠Ｅ＝２２．５°． 解法二：∵四边形 ＡＢＣＤ是正方形， ∴∠ＡＣＤ＝∠ＤＡＣ＝４５°，∠ＤＣＥ＝９０° ∴∠ＡＣＥ＝４５°＋９０°＝１３５°． ∵ＡＣ＝ＥＣ， ∴∠ＣＡＥ＝２２．５°． ∴∠ＤＡＦ＝４５°－２２．５°＝２２．５°． １９．解：（１）∵Ａ（ｍ，２）在一次函数 ｙ＝－ｘ＋１的图象上， ∴ｍ＝－１． ∴Ａ（－１，２）． ∵Ａ（－１，２）在反比例函数 ｙ＝ｋ ｘ的图象上， ∴ｋ＝－２． ∴反比例函数的解析式为 ｙ＝－２ ｘ． （２）－１＜ｘ＜０或 ｘ＞２． ２０．解：如解图所示，ＡＧ，ＤＨ分别是∠ＢＡＣ与∠ＥＤＦ的角平 分线． 第 ２０题解图 已知：如解图，△ＡＢＣ∽△ＤＥＦ，ＡＢ ＤＥ＝ＢＣ ＥＦ＝ＡＣ ＤＦ＝ｋ，ＡＧ，ＤＨ 分别是∠ＢＡＣ与∠ＥＤＦ的角平分线． 求证：ＡＧ ＤＨ＝ｋ． 证明：∵ＡＧ，ＤＨ分别是∠ＢＡＣ与∠ＥＤＦ的角平分线， ∴∠ＢＡＧ＝１ ２∠ＢＡＣ，∠ＥＤＨ＝１ ２∠ＥＤＦ． ∵△ＡＢＣ∽△ＤＥＦ， ∴∠ＢＡＣ＝∠ＥＤＦ，∠Ｂ＝∠Ｅ． ∴∠ＢＡＧ＝∠ＥＤＨ． ∴△ＡＢＧ∽△ＤＥＨ． ∴ＡＧ ＤＨ＝ＡＢ ＤＥ＝ｋ． ２１．解：依题意得 ＡＢ＝３０步，ＣＤ＝７５０步． 解法一：设 ＡＥ为 ｘ步，则正方形边长为 ２ｘ步，根据题意， Ｒｔ△ＡＢＥ∽Ｒｔ△ＣＥＤ． ∴ＡＢ ＣＥ＝ＡＥ ＣＤ． 即３０ ｘ＝ ｘ ７５０． 解得 ｘ１ ＝１５０，ｘ２ ＝－１５０（不合题意，舍去）． ∴２ｘ＝３００ ∴正方形城池的边长为 ３００步． 解法二：设正方形城池的边长为 ｘ步，根据题意， Ｒｔ△ＡＢＥ∽Ｒｔ△ＣＥＤ． ∴ＡＢ ＣＥ＝ＡＥ ＣＤ． 即 ３０ １ ２ｘ ＝ １ ２ｘ ７５０． 解得 ｘ１ ＝３００，ｘ２ ＝－３００（不合题意，舍去）． ∴正方形城池的边长为 ３００步． ２２．解：（１）３； （２）解法一：由表格可得，二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ顶点坐 标是（１，－１）， ∴ｙ＝ａ（ｘ－１）２ －１． ∵当 ｘ＝０时，ｙ＝０， ∴ａ＝１． ∴这个二次函数的解析式为 ｙ＝（ｘ－１）２ －１＝ ｘ２ －２ｘ． 解法二：由题意得 ｃ＝０ ａ＋ｂ＋ｃ＝－１ ４ａ＋２ｂ＋ｃ{ ＝０ ， ∴ ａ＝１ ｂ＝－２ ｃ{ ＝０ ． ∴这个二次函数的解析式为 ｙ＝ｘ２ －２ｘ． 解法三：由表格可得 ｙ＝ａｘ（ｘ－２）， ∵当 ｘ＝１时，ｙ＝－１， ∴ａ＝１． ∴这个二次函数的解析式为 ｙ＝ｘ２ －２ｘ． （３）ｎ＞０． ２３．解：（１） 进价 （元） 售价 （元） 每件利润 （元） 销量 （个） 总利润 （元                                                                    ） ０１ 降价前 降价后 ８０－ｘ ３０－ｘ １６０＋２０· ｘ ２ 或 １６０＋１０ｘ （８０－５０－ｘ） （１６０＋２０· ｘ ２）或 （３０－ｘ）（１６０＋ １０ｘ） （２）（８０－５０－ｘ）（１６０＋２０· ｘ ２）＝５２００， 解得 ｘ１ ＝１０，ｘ２ ＝４（不合题意，舍去）． 答：每个电子产品应降价 １０元． ２４．解：（１）由折叠的性质可知 ＤＣ＝ＥＣ，∠ＤＣＧ＝∠ＥＣＧ． ∵ＥＧ∥ＣＤ， ∴∠ＤＣＧ＝∠ＥＧＣ． ∴∠ＥＧＣ＝∠ＥＣＧ． ∴ＥＧ＝ＥＣ． ∴ＥＧ＝ＤＣ． ∴四边形 ＥＣＤＧ是平行四边形． ∵ＥＧ＝ＥＣ， 第 ２４题解图 ∴ＥＣＤＧ是菱形； （２）如解图，连接 ＥＤ交 ＡＣ于点 Ｏ， ∵四边形 ＥＣＤＧ是菱形， ∴ＥＤ⊥ＡＣ，ＯＣ＝１ ２ＣＧ． ∵四边形 ＡＢＣＤ是矩形， ∴∠ＡＤＣ＝９０°． ∴△ＤＣＯ∽△ＡＣＤ． ∴ＤＣ ＡＣ＝ＯＣ ＤＣ． ∴ＤＣ２ ＝ＯＣ·ＡＣ． 设 ＯＣ＝ｘ，则 ＣＧ＝２ｘ，ＡＣ＝２ｘ＋１４ ５， ∴３６＝ｘ（２ｘ＋１４ ５）． 解得 ｘ１ ＝１８ ５，ｘ２ ＝－５（不合题意，舍去）． 解法一：∵ＥＧ∥ＣＤ， ∴ＥＨ∥ＡＢ． ∴△ＣＧＨ∽△ＣＡＢ． ∴ＧＨ ＡＢ＝ＣＧ ＣＡ，即ＧＨ ６ ＝ ３６ ５ １０． ∴ＧＨ＝１０８ ２５． ∴ＥＨ＝ＥＧ－ＧＨ＝６－１０８ ２５＝４２ ２５． 解法二：∵ＣＤ＝６，ＡＣ＝１０，∠ＡＤＣ＝９０°， ∴ＡＤ＝ ＡＤ２ ＋ＣＤ槡 ２ ＝８． 由折叠可知，∠ＤＡＣ＝∠ＣＡＦ． ∵ＡＤ∥ＢＣ， ∴∠ＤＡＣ＝∠ＡＣＢ． ∴ＡＦ＝ＣＦ． ∴△ＡＦＢ≌△ＣＦＥ． 设 ＥＦ＝ｘ，则 ＢＦ＝ｘ，ＣＦ＝８－ｘ． ∴（８－ｘ）２ －ｘ２ ＝６２． 解得 ｘ＝７ ４． ∴ＣＦ＝２５ ４． ∵Ｓ△ＣＥＦ ＝ＥＦ·ＣＦ ２ ，Ｓ△ＣＥＦ ＝ＣＦ·ＥＨ ２ ， ∴ＥＨ＝ＥＦ·ＣＦ ＣＦ ＝ ７ ４ ×６ ２５ ４ ＝４２ ２５． ２５．解：（１）当 ｙ＝０，ｍｘ２ ＋（ｍ－２）ｘ－２ｍ＋２＝０， Δ＝（ｍ－２）２ －４ｍ（－２ｍ＋２）＝９ｍ２ －１２ｍ＋４＝（３ｍ－ ２）２≥０， ∴抛物线 ｙ＝ｍｘ２ ＋（ｍ－２）ｘ－２ｍ＋２与 ｘ轴有交点； （２）①当 ｙ＝０时，ｍｘ２ ＋（ｍ－２）ｘ－２ｍ＋２＝０， 十字相乘法解得：ｘ＝１或 ｘ＝２－２ｍ ｍ ， ∵点 Ａ在点 Ｂ的右侧， ∴ｘ１ ＞ｘ２， ∵ｘ１ ＋２ｘ２ ＝１， 当 ｘ１ ＝１，ｘ２ ＝２－２ｍ ｍ 时，１＋２×２－２ｍ ｍ ＝１，解得 ｍ＝１． 此时 ｘ１ ＝１，ｘ２ ＝０，满足 ｘ１ ＞ｘ２，故 ｍ＝１符合题意． 当 ｘ１ ＝２－２ｍ ｍ ，ｘ２ ＝１时，２－２ｍ ｍ ＋１×２＝１，解得 ｍ＝２． 此时 ｘ１ ＝－２，ｘ２ ＝１，与 ｘ１ ＞ｘ２ 矛盾，故 ｍ＝２不符合 题意． ∴ｍ＝１． ②ｍ＝１时，抛物线解析式为 ｙ＝ｘ２ －ｘ， ∵点 Ｇ（ｎ，－４ ３ｎ－３５ ９）， ∴点 Ｇ在直线 ｙ＝－４ ３ｘ－３５ ９上， 设与直线 ｙ＝－４ ３ｘ－３５ ９平行的直线 ｌ：ｙ＝－４ ３ｘ＋ｂ． 当直线 ｌ：ｙ＝－４ ３ｘ＋ｂ与抛物线只有一个交点时，ＰＧ有 最小值， 第 ２５题解图 此时 ｙ＝－４ ３ｘ＋ｂ ｙ＝ｘ２ －{ ｘ ，方程 ｘ２ － ｘ＝－４ ３ｘ＋ｂ的 Δ＝０， 解得 ｂ＝－１ ３６， 如解图，直线 ｌ与 ｘ、ｙ轴交于 Ｄ、Ｍ点，直线 ｙ＝－ ４ ３ｘ－３５ ９ 与 ｙ轴交于点 Ｎ， ∴Ｄ（－１ ４８，０），Ｍ（０，－１ ３６）， ∴ＯＤ＝１ ４８，ＯＭ＝１ ３６， ∴ＭＮ＝－１ ３６－（－３５ ９）＝１３９ ３６， ∴ＤＭ＝ ＯＤ２ ＋ＯＭ槡 ２ ＝ ５ １４４                                                                        ， １１ 过点 Ｍ做 ＭＨ垂直直线 ｙ＝－４ ３ｘ－３５ ９， 过 Ｐ做 ＰＧ垂直直线 ｙ＝－４ ３ｘ－３５ ９，此时 ＰＧ最小，且 ＰＧ ＝ＭＨ， 此时△ＤＯＭ∽△ＭＨＮ， ∴ＤＭ ＭＮ＝ＤＯ ＭＨ，即 ５ １４４ １３９ ３６ ＝ １ ４８ ＭＨ， ∴ＰＧ＝ＭＨ＝１３９ ６０        ． ２１ ２０１８－２０１９学年福建省莆田市九年级（上）期末数学试卷 参考答案与试题解析 一、选择题（每小题 ４分，共 ４０分） １．Ａ　２．Ａ　３．Ｃ　４．Ｃ　５．Ｂ　６．Ｂ　７．Ｂ　８．Ｄ ９．Ｃ　１０．Ｂ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．４．５　１２．２５　１３．＞；一；减小 １４．ｘ≤５　１５．１１０°　１６．４ 三、解答题（共 ９小题，共 ８６分） １７．（１）证明：∵ＣＦ∥ＡＢ， ∴∠ＣＦＥ＝∠ＤＡＥ，∠ＦＣＥ＝∠ＡＤＥ， ∵Ｅ为 ＣＤ的中点， ∴ＣＥ＝ＤＥ， 在△ＥＣＦ和△ＥＤＡ中， ∠ＣＦＥ＝∠ＤＡＥ ∠ＦＣＥ＝∠ＡＤＥ ＣＥ＝{ ＤＥ ， ∴△ＥＣＦ≌△ＥＤＡ（ＡＡＳ）， ∴ＣＦ＝ＡＤ； （２）解：四边形 ＣＤＢＦ为正方形，理由如下： ∵ＣＤ是 ＡＢ边上的中线， ∴ＡＤ＝ＢＤ， ∵ＣＦ＝ＡＤ， ∴ＣＦ＝ＢＤ． ∵ＣＦ＝ＢＤ，ＣＦ∥ＢＤ， ∴四边形 ＣＤＢＦ为平行四边形， ∵ＣＡ＝ＣＢ，ＣＤ为 ＡＢ边上的中线， ∴ＣＤ⊥ＡＢ，即∠ＢＤＣ＝９０°， ∴四边形 ＣＤＢＦ为矩形， ∵等腰直角△ＡＢＣ中，ＣＤ为斜边上的中线， ∴ＣＤ＝１ ２ＡＢ＝ＢＤ， ∴四边形 ＣＤＢＦ为正方形． １８．解：（１）设平均每次下调的百分率是 ｘ，根据题意列方 程得， ５０００（１－ｘ）２ ＝４０５０， 解得：ｘ１ ＝１０％，ｘ２ ＝１．９（不合题意，舍去）； 答：平均每次下调的百分率为 １０％； （２）方案一的房款是：４０５０×１００×０．９８＝３９６９００（元）； 方案二的房款是：４０５０×１００－１．５×１００×１２×２＝４０１４００ （元） ∵３９６９００元 ＜４０１４００元， ∴方案①更优惠． １９．（１）解：如解图所示：ＡＤ即为所求； 第 １９题解图 （２）证明：∵∠ＢＡＣ＝９０°， ∴∠ＢＡＤ＋∠ＣＡＤ＝９０°， ∵ＡＤ是△ＡＢＣ的高，ＡＤ⊥ＢＣ， ∴∠ＣＤＡ＝９０°， 在 Ｒｔ△ＣＡＤ中， ∠Ｃ＋∠ＣＡＤ＝９０°， ∴∠Ｃ＝∠ＢＡＤ． ２０．解：（１）画出的图形如解图①所示，△ＤＥＦ即为所求： 第 ２０题解图 （２）画出的图形如解图 ② 所示，四边形 Ａ′Ｂ′Ｃ′Ｄ′即为 所求． ２１．解：（１）所有等可能的结果共有 ３种，恰好选中 Ｄ队的结 果有 １种， ∴恰好选中 Ｄ队的概率 Ｐ＝１ ３； （２）画树状图得： 所有等可能的结果共有 １２种，恰好选中 Ｂ、Ｃ两队进行比 赛的结果有 ２种， ∴Ｐ（恰好选中 Ｂ、Ｃ两队进行比赛）＝２ １２＝１ ６． ２２．解：（１）设这两年该县投入教育经费的年平均增长率为 ｘ， 根据题意得： ６０００（１＋ｘ）２ ＝８６４０ 解得：ｘ１ ＝０．２＝２０％，ｘ２ ＝－２．２（不合题意，舍去）， 答：这两年该县投入教育经费的年平均增长率为 ２０％； （２）∵２０１６年该县投入教育经费为 ８６４０万元，且增长率 为 ２０％， ∴２０１７年该县投入教育经费为：８６４０×（１＋０．２）＝１０３６８ （万元）， 答：预计 ２０１７年该县投入教育经费约 １０３６８万元． ２３．解：（１）作图如解图： 第 ２３题解图 （２）∵ＣＤ∥ＡＢ、Ｃ′Ｄ′∥ＡＢ                                                                    ， ３１ ∴ＣＤ ＡＢ＝ＥＤ ＥＢ、Ｃ′Ｄ′ ＡＢ ＝Ｄ′Ｅ′ ＢＥ′， ∴ＥＤ ＥＢ＝Ｄ′Ｅ′ ＢＥ′， ∵ＤＥ＝ＣＤ＝１．５米，Ｄ′Ｅ′＝２ＣＤ＝３米， ∴ １．５ ＢＤ＋１．５＝ ３ ＢＤ＋６， 解得：ＢＤ＝３， ∴ＡＢ＝ＢＥ＝ＢＤ＋ＤＥ＝３＋１．５＝４．５米． ２４．解：（１）将 Ｐ（４，３）代入函数 ｙ＝ｋ ｘ，得：ｋ＝４×３＝１２． ∴反比例函数为 ｙ＝１２ ｘ， ∵△ＡＯＢ和△ＰＡＢ都可以看作以 ＡＢ为底，它们的面积 相等， ∴它们的底 ＡＢ边上的高也相等，即点 Ｏ和点 Ｐ到直线 ＡＢ的距离相等， ∴ｘＰ ＝２ｘＢ， ∵Ｐ（４，３），即 ｘＰ ＝４， ∴ｘＢ ＝２， 代入 ｙ＝１２ ｘ，得：ｙ＝６， ∴Ｂ（２，６）； （２）设直线 ＢＰ的解析式为 ｙ＝ａｘ＋ｂ， 分别代入 Ｂ（２，６）、Ｐ（４，３）， 得： ２ａ＋ｂ＝６ ４ａ＋ｂ{ ＝３， 解得 ａ＝－３ ２ ｂ{ ＝９ ， ∴直线 ＢＰ的解析式为 ｙ＝－３ ２ ｘ＋９； （３）由图知，在第一象限内，反比例函数大于一次函数的 ｘ 的取值范围是 ０＜ｘ＜２或 ｘ＞４． ２５．解：（１）根据题意得：ＭＡ＝ｘ，ＯＮ＝１．２５ｘ， 在 Ｒｔ△ＯＡＢ中，由 勾 股 定 理 得：ＯＢ＝ ＯＡ２ ＋ＡＢ槡 ２ ＝ ４２ ＋３槡 ２ ＝５， 作 ＮＰ⊥ＯＡ于 Ｐ，如解图①所示：则 ＮＰ∥ＡＢ， ∴△ＯＰＮ∽△ＯＡＢ， ∴ＰＮ ＡＢ＝ＯＰ ＯＡ＝ＯＮ ＯＢ， 即ＰＮ ３ ＝ＯＰ ４ ＝１．２５ｘ ５ ， 解得：ＯＰ＝ｘ，ＰＮ＝３ ４ｘ， ∴点 Ｎ的坐标是（ｘ，３ ４ｘ）； （２）在△ＯＭＮ中，ＯＭ＝４－ｘ，ＯＭ边上的高 ＰＮ＝３ ４ｘ， ∴Ｓ＝１ ２ＯＭ·ＰＮ＝１ ２（４－ｘ）· ３ ４ｘ＝－３ ８ｘ２ ＋３ ２ｘ， ∴Ｓ与 ｘ之间的函数表达式为 Ｓ＝－３ ８ｘ２ ＋３ ２ｘ（０＜ｘ＜ ４）， 配方得：Ｓ＝－３ ８（ｘ－２）２ ＋３ ２， ∵ －３ ８ ＜０， ∴Ｓ有最大值， 当 ｘ＝２时，Ｓ有最大值，最大值是 ３ ２； （３）存在某一时刻，使△ＯＭＮ是直角三角形，理由如下： 分两种情况：①若∠ＯＭＮ＝９０°，如解图②所示： 则 ＭＮ∥ＡＢ， 此时 ＯＭ＝４－ｘ，ＯＮ＝１．２５ｘ， ∵ＭＮ∥ＡＢ， ∴△ＯＭＮ∽△ＯＡＢ， ∴ＯＭ ＯＡ＝ＯＮ ＯＢ， 即４－ｘ ４ ＝１．２５ｘ ５ ， 解得：ｘ＝２； ②若∠ＯＮＭ＝９０°，如解图③所示： 则∠ＯＮＭ＝∠ＯＡＢ， 此时 ＯＭ＝４－ｘ，ＯＮ＝１．２５ｘ， ∵∠ＯＮＭ＝∠ＯＡＢ，∠ＭＯＮ＝∠ＢＯＡ， ∴△ＯＭＮ∽△ＯＢＡ， ∴ＯＭ ＯＢ＝ＯＮ ＯＡ， 即４－ｘ ５ ＝１．２５ｘ ４ ， 解得：ｘ＝６４ ４１； 综上所述：ｘ的值是 ２秒或 ６４ ４１秒时，△ＯＭＮ是直角三 角形． 图① 　　 图② 图③ 第 ２５                                                                 题解图 ４１ 宁德市 ２０１８－２０１９学年度第一学期期末九年级质量检测 数学试题参考答案及评分标准 一、选择题：本题共 １０小题，每小题 ４分，共 ４０分） １．Ｄ　２．Ａ　３．Ｄ　４．Ｂ　５．Ａ　６．Ｄ　７．Ｂ　８．Ｃ　９．Ａ １０．Ｂ 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分． １１．中心投影　１２．ｘ＝－２　１３．８１　１４．５ ２ １５．ｙ＝－２（ｘ－２）２ －１或 ｙ＝－２ｘ２ ＋８ｘ－９ １６．－９ 三、解答题：本题共 ９小题，共 ８６分． １７．解：ｘ２ －４ｘ＝－１． （１分）!!!!!!!!!!!!! ｘ２ －４ｘ＋４＝－１＋４． （３分）!!!!!!!!!! （ｘ－２）２ ＝３． （４分）!!!!!!!!!!!!!! ｘ 槡－２＝± ３． （５分）!!!!!!!!!!!!!! ∴ｘ１ 槡＝２＋ ３，ｘ２ 槡＝２－ ３． （７分）!!!!!!!!!! １８．解：∵△ＡＤＥ∽△ＡＢＣ， ∴ＡＤ ＡＢ＝ＡＥ ＡＣ． （３分）!!!!!!!!!!!!!!!! ∵ＡＤ＝６，ＡＥ＝４，ＡＢ＝１２， ∴ ６ １２＝４ ＡＣ． （４分）!!!!!!!!!!!!!!!! ∴ＡＣ＝８． （６分）!!!!!!!!!!!!!!!! ∴ＣＤ＝ＡＣ－ＡＤ＝８－６＝２． （７分）!!!!!!!!! １９．解：方案一：∵转盘 Ａ被平均分成 ３份，其中红色区域占 １份， ∴Ｐ（获得奖品）＝１ ３． （２分）!!!!!!!!!!! 方案二：∵转盘 Ｂ被平均分成 ３份，分别记为红１，红２，蓝， ∴可列表为： 　　第 ２次 第 １次　　 红１ 红２ 蓝 红１ （红１，红１） （红１，红２） （红１，蓝） 红２ （红２，红１） （红２，红２） （红２，蓝） 蓝 （蓝，红１） （蓝，红２） （蓝，蓝） 由表格可知，一共有 ９种等可能结果，其中两次都转出红 色的结果有 ４种，分别是（红１，红１），（红１，红２），（红２， 红１），（红２，红２）． ∴Ｐ（获得奖品）＝４ ９． （７分）!!!!!!!!!!! ∵ １ ３ ＜４ ９， ∴选择方案二． （８分）!!!!!!!!!!!!!! ２０．解：已知：在ＡＢＣＤ中，ＤＥ⊥ＡＢ，ＤＦ⊥ＢＣ，ＤＥ＝ＤＦ． 求证：ＡＢＣＤ是菱形． （２分）!!!!!!!!!!! 证法一： ∵四边形 ＡＢＣＤ是平行四边形， ∴∠Ａ＝∠Ｃ． ∵ＤＥ⊥ＡＢ，ＤＦ⊥ＢＣ， ∴∠ＤＥＡ＝∠ＤＦＣ＝９０°． 又∵ ＤＥ＝ＤＦ， （５分）!!!!!!!!!!!!!! ∴△ＤＡＥ≌△ＤＣＦ． （６分）!!!!!!!!!!!! ∴ ＤＡ＝ＤＣ． ∴ＡＢＣＤ是菱形． （８分）!!!!!!!!!!!! 证法二： ∵ＤＥ⊥ＡＢ，ＤＦ⊥ＢＣ， ∴ ＳＡＢＣＤ ＝ＡＢ·ＤＥ＝ＢＣ·ＤＦ． （５分）!!!!!!! ∵ ＤＥ＝ＤＦ， ∴ＡＢ＝ＢＣ． （７分）!!!!!!!!!!!!!!!! ∴ＡＢＣＤ是菱形． （８分）!!!!!!!!!!!! ２１．解：（１）将 Ａ（１，ｍ）代入 ｙ＝ｘ２ ＋２ｘ＋２得， ｍ＝５． （２分）!!!!!!!!!!!!!!!!!! 将 Ａ（１，５）代入 ｙ＝ｋ ｘ得， ｋ＝５． （４分）!!!!!!!!!!!!!!!!!! ∴反比例函数的表达式为 ｙ＝５ ｘ． （５分）!!!!!! （２）∵ｙ＝ｘ２ ＋２ｘ＋２＝（ｘ＋１）２ ＋１， ∴抛物线的对称轴为直线 ｘ＝－１，且开口向上． ∴当 ｘ≤ －１时，二次函数的值随 ｘ的增大而减小， （７分） !! !!!!!!!!!!!!!!!!!!! 又∵当 ｘ＜０时，ｙ＝５ ｘ函数值随 ｘ的增大而减小． （９分） !! !!!!!!!!!!!!!!!!!!! ∴当 ｘ≤ －１时，二次函数与反比例函数的值都随 ｘ的增 大而减小． （１０分）!!!!!!!!!!!!!!!! ２２．解 ：如解图，过点 Ｅ作 ＥＦ⊥ＢＣ于点 Ｆ， （１分）!!!! 第 ２２题解图 在 Ｒｔ△ＢＥＦ中，ｓｉｎ∠ＥＢＦ＝ＥＦ ＢＥ， ∴ＥＦ＝ＢＥ·ｓｉｎ∠ＥＢＦ＝３×ｓｉｎ６８° ≈３×０．９２７≈２．７８１． （４分）!!!!!!!!! ∵∠ＢＣＥ＝∠ＡＥＣ－∠ＡＢＣ＝８７°－６８°＝１９°， ∴∠ＣＥＦ＝９０°－∠ＢＣＥ＝７１°． （６分）!!!!!!!! 在 Ｒｔ△ＣＥＦ中，ｃｏｓ∠ＦＥＣ＝ＦＥ ＥＣ， ∴ＥＣ＝ ＥＦ ｃｏｓ∠ＦＥＣ＝２．７８１ ｃｏｓ７１°≈２．７８１ ０．３２６≈８．５． （９分）                                                                    !!! ５１ ∴ＣＤ＝ＤＥ＋ＥＣ≈２＋８．５＝１０．５． 答：支撑板 ＣＤ的长约为 １０．５ｃｍ． （１０分）!!!!!! ２３．解：（１）１０，１０＋０．２ｘ，３０００－１０ｘ； （３分）!!!!!!! （２）依题意，得 （１０＋０．２ｘ）（３０００－１０ｘ）－７×３０００＝２９０００． （７分）! 解得 ｘ１ ＝５０或 ｘ２ ＝２００． （９分）!!!!!!!!!! ∵ｘ２ ＝２００＞１００，不合题意，舍去， ∴ｘ＝５０． 答：将这批槟榔芋贮藏 ５０天后一次性出售最终可获得总 利润 ２９０００元． （１０分）!!!!!!!!!!!!!! （方程也可列为 （１０＋０．２ｘ－７）（３０００－１０ｘ）－７×１０ｘ＝ ２９０００） ２４．解：（１）∵ 四边形 ＡＢＣＤ是矩形， ∴∠ＢＡＤ＝∠Ｃ＝∠ＡＤＣ＝∠ＡＢＣ＝９０°． （１分）!!!! 由折叠的性质可得∠ＢＧＰ＝∠Ｃ＝∠ＡＤＣ＝９０°． ∴∠ＧＭＮ＋∠ＧＮＭ＝∠ＤＮＰ ＋∠ＤＰＮ＝９０°． ∵∠ＧＮＭ＝∠ＤＮＰ， ∴∠ＧＭＮ＝∠ＤＰＮ． （２分）!!!!!!!!!!!! ∴∠ＡＭＢ＝∠ＧＭＮ＝∠ＤＰＮ． ∴ △ＡＢＭ∽△ＤＮＰ； （４分）!!!!!!!!!!!! （２）如解图①，过点 Ｇ作直线 ＥＦ⊥ＣＤ交 ＣＤ的延长线于 点 Ｆ，交 ＢＡ的延长线于点 Ｅ． 第 ２４题解图① ∵∠ＡＢＣ＝∠Ｃ＝９０°， ∴ 四边形 ＢＣＦＥ是矩形． ∴ ＥＦ＝ＢＣ＝１０，ＢＥ＝ＣＦ． ∵ ＧＦ＝５， ∴ ＥＧ＝５． 由折叠的性质可得 ＢＧ＝ＢＣ＝１０，ＧＰ＝ＰＣ． 在 Ｒｔ△ＢＥＧ中，由 勾 股 定 理，得 ＢＥ＝ ＢＧ２ －ＥＧ槡 ２ ＝ １０２ －５槡 ２ 槡＝５ ３． （６分）!!!!!!!!!!!!! 方法一：∴ＦＣ 槡＝５ ３． 设 ＣＰ＝ｘ，则 ＧＰ＝ｘ，ＦＰ 槡＝５ ３ －ｘ． 在 Ｒｔ△ＧＦＰ中，由勾股定理得 ＦＰ２ ＋ＧＦ２ ＝ＧＰ２． ∴（ 槡５ ３－ｘ）２ ＋５２ ＝ｘ２． （８分）!!!!!!!!!!! 解得 ｘ＝ 槡１０ ３ ３ ．即 ＣＰ＝ 槡１０ ３ ３ ． （９分）!!!!!!!! 方法二：∵∠ＥＧＢ＋∠ＦＧＰ＝∠ＥＧＢ＋∠ＥＢＧ＝９０°， ∴ ∠ＥＢＧ＝∠ＦＧＰ． 又∵∠ＧＥＢ＝∠ＰＦＧ＝９０°， ∴△ＧＥＢ∽△ＰＦＧ． ∴ＢＧ ＧＰ＝ＢＥ ＧＦ． ∴１０ ＧＰ＝ 槡５ ３ ５ ． （８分）!!!!!!!!!!!!!!! 解得 ＧＰ＝ 槡１０ ３ ３ ． ∴ＣＰ＝ 槡１０ ３ ３ ． （９分）!!!!!!!!!!!!!!! （３）存在．尺规作图如解图所示： （１３分）!!!!!! 图② 　　 图③ 第 ２４题解图 ∴解图②、解图③中的△ＢＧＰ即为所求． ２５．解：（１）将 Ａ（－４，０），Ｂ（６，０）代入 ｙ＝ａｘ２ ＋ｂｘ＋３得 １６ａ－４ｂ＋３＝０， ３６ａ＋６ｂ＋３＝０{ ， （２分）!!!!!!!!!!!!! 解得 ａ＝－１ ８， ｂ＝１ ４ { ． ∴ 该抛物线的函数表达式为 ｙ＝－１ ８ｘ２ ＋１ ４ｘ＋３； （４分） !! !!!!!!!!!!!!!!!!!!! （２）令 ｘ＝０，则 ｙ＝３，∴Ｃ（０，３）． 当点 Ｇ与点 Ｃ重合时，点 Ｇ的坐标为（０，３）． （５分）!! 将 ｙ＝３代入 ｙ＝－１ ８ｘ２ ＋１ ４ｘ＋３得 －１ ８ｘ２ ＋１ ４ｘ＋３＝３． 解得 ｘ１ ＝０（舍去），ｘ２ ＝２． ∴点 Ｄ的坐标为（２，３）． （７分）!!!!!!!!!! ∴ＧＤ＝２，ＤＥ＝３． ∴Ｓ矩形ＤＥＦＧ ＝ＤＧ·ＤＥ＝２×３＝６； （８分）!!!!!!! （３）设直线 ＢＣ的表达式为 ｙ＝ｋｘ＋ｍ（ｋ≠０）， 将 Ｂ（６，０），Ｃ（０，３）代入上式， 得 ６ｋ＋ｍ＝０， ｍ＝３{ ， 解得 ｋ＝－１ ２ ｍ{ ＝３ ． ∴直线 ＢＣ的表达式为 ｙ＝－１ ２ｘ＋３． （９分）!!!! 设点 Ｄ的横坐标为 ｎ，由对称性得 ２≤ｎ≤６， ∴点 Ｄ，Ｎ的坐标分别分 Ｄ（ｎ，－１ ８ｎ２ ＋１ ４ｎ＋３），Ｎ（ｎ， －１ ２ｎ＋３）． ∴ＤＮ＝－１ ８ｎ２ ＋１ ４ｎ＋３－（－１ ２ｎ＋３）＝－１ ８（ｎ－３）２ ＋９ ８                                                                        ． ６１ ∴当 ｎ＝３，ＤＮ取得最大值为 ９ ８． （１０分）!!!!!! ∵ＤＧ∥ｘ轴， ∴ ∠ＤＭＮ＝∠ＯＢＣ． 又∵∠ＭＤＮ＝∠ＢＯＣ＝９０°， ∴△ＤＭＮ∽△ＯＢＣ． （１１分）!!!!!!!!!!! ∴Ｓ△ＤＭＮ Ｓ△ＯＢＣ ＝（ＤＮ ＯＣ）２． ∴当 ＤＮ最大时，△ＤＭＮ的面积也最大． （１２分）!!! ∵Ｓ△ＯＢＣ ＝１ ２ ×３×６＝９， ∴Ｓ△ＤＭＮ ＝Ｓ△ＯＢＣ ×（ＤＮ ＯＣ）２ ＝９×（９ ８ ÷３）２ ＝８１ ６４． ∴△ＤＭＮ面积的最大值为８１ ６４． （１３分）           !!!!!!! ７１ ２０１８－２０１９学年龙岩第一学期期末九年级数学 参考答案及评分标准 一、选择题（本大题共 １０题，每题 ４分，共 ４０分） １．Ｂ　２．Ｄ　３．Ｃ　４．Ａ　５．Ｂ　６．Ｃ　７．Ｃ　８．Ｄ ９．Ａ　１０．Ａ 二、填空题（本大题共 ６题，每题 ４分，共 ２４分） １１．２３ ５０　１２．１２π　１３．（－３，１）　１４．ｙ＝２（ｘ＋２）２ －１ １５．ｘ２ ＋６ｘ－３２＝０　１６．ｘ＜－２或 ｘ＞８ 三、解答题（本大题共 ９小题，共 ８６分） １７．解：ｘ２ ＋２ｘ＋１＝２， ２分!!!!!!!!!!!!!! （ｘ＋１）２ ＝２， ４分!!!!!!!!!!!!!!!! ｘ１ 槡＝－１＋ ２，ｘ２ 槡＝－１－ ２． ８分!!!!!!!!!! １８．解：（１）如解图，△ＡＢ１Ｃ１ 即为所求； ４分!!!!!!! 第 １８题解图 （２）∵ＡＢ＝ ３２ ＋４槡 ２ ＝５， ６分!!!!!!!!!!! ∴ｌＢＢ１ ＝９０ １８０×π×５＝５ ２π． ８分!!!!!!!!!!! １９．解：原式 ＝（２ｘ＋１ ｘ －ｘ ｘ）÷（ｘ＋１）（ｘ－１） ｘ ＝ｘ＋１ ｘ × ｘ （ｘ＋１）（ｘ－１） ＝ １ ｘ－１． ５分!!!!!!!!!!!!!!! 当 ｘ 槡＝ ２＋１时， 原式 ＝ １ 槡２＋１－１ ＝槡２ ２． ８分!!!!!!!!!!!! ２０．解：（１）∵有汉字“美”、“丽”、“龙”、“岩”的四个小球，任 取一球，共有 ４种不同结果， ∴球上汉字是“美”的概率为 Ｐ＝１ ４； ３分!!!!!! （２）列表如下： 美 丽 龙 岩 美 ／ （丽，美） （龙，美） （岩，美） 丽 （美，丽） ／ （龙，丽） （岩，丽） 龙 （美，龙） （丽，龙） ／ （岩，龙） 岩 （美，岩） （丽，岩） （龙，岩） ／ 画树状图如解图： 第 ２０题解图 ６分!!!!!!!!!!!!!!!!!!!!!! 由列表或画树状图可得，所有等可能的情况有 １２种，其中 取出的两个球上的汉字恰能组成“美丽”或“龙岩”的情况 有 ４种，则 Ｐ１ ＝４ １２＝１ ３． ８分!!!!!!!!!!! ２１．解：（１）如解图所示，射线 ＡＥ就是所求作的角平分线； ３分!!!!!!!!!!!!!!!!!!!!!! 第 ２１题解图 （２）如解图，连接 ＯＥ交 ＢＣ于点 Ｆ，连接 ＯＣ、ＣＥ， ４分! ∵ＡＥ平分∠ＢＡＣ， ∴ ) ＢＥ＝ ) ＣＥ ∴ＯＥ⊥ＢＣ，ＥＦ＝３， ∴ＯＦ＝５－３＝２， ６分!!!!!!!!!!!!!!! 在 Ｒｔ△ＯＦＣ中，由 勾 股 定 理 可 得 ＦＣ＝ ＯＣ２ －ＯＦ槡 ２ 槡＝ ２１， 在 Ｒｔ△ＥＦＣ中，由 勾 股 定 理 可 得 ＣＥ＝ ＥＦ２ ＋ＦＣ槡 ２ ＝ 槡３０． ８分!!!!!!!!!!!!!!!!!!! ２２．解：（１）当 ｘ＝６时，ｙ１ ＝３，ｙ２ ＝１， ∵ｙ１ －ｙ２ ＝３－１＝２， ∴６月份出售这种蔬菜每千克的收益是 ２元； ２分!!! （２）设 ｙ１ ＝ｍｘ＋ｎ，ｙ２ ＝ａ（ｘ－６）２ ＋１． ４分!!!!!! 将（３，５）、（６，３）代入 ｙ１ ＝ｍｘ＋ｎ， 解得： ｍ＝－２ ３ ｎ{ ＝７ ， ∴ｙ１ ＝－２ ３ｘ＋７． ４分!!!!!!!!!!!!!! 将（３，４）代入 ｙ２ ＝ａ（ｘ－６）２ ＋１， ４＝ａ（３－６）２ ＋１，解得：ａ＝１ ３， ∴ｙ２ ＝１ ３（ｘ－６）２ ＋１ ＝１ ３ｘ２ －４ｘ＋１３； ６分!!!!!!!!!!!! （３）５月份出售这种蔬菜，每千克的收益最大，理由： ∵ｙ１ －ｙ２ ＝－２ ３ｘ＋７－（１ ３ｘ２ －４ｘ＋１３） ＝－１ ３ｘ２ ＋１０ ３ｘ－６ ＝－１ ３（ｘ－５）２ ＋７ ３， ８分!!!!!!!! ∴当 ｘ＝５时，ｙ１ －ｙ２ 取最大值，最大值为 ７ ３， 即 ５月份出售这种蔬菜，每千克的收益最大． １０分!!! ２３．（１）证明：如解图，连接                                                                   ＯＤ． ８１ 第 ２３题解图 ∵ＯＤ＝ＯＡ， ∴∠ＯＡＤ＝∠ＯＤＡ， ∵ＥＦ垂直平分 ＤＢ，∴ ＥＤ＝ＥＢ， ∠ＥＤＢ＝∠ＥＢＤ， 又∵∠Ａ＋∠Ｂ＝９０°， ∴∠ＯＤＡ＋∠ＥＤＢ＝９０°， ２分!!!!!!!!!!! ∴∠ＯＤＥ＝９０°，即 ＯＤ⊥ＤＥ， ∵点 Ｄ在⊙Ｏ上， ∴ＤＥ是⊙Ｏ的切线； ４分!!!!!!!!!!!!! （２）解：∵∠Ｂ＝３０°， ∴∠Ａ＝６０°， ∴△ＯＡＤ是等边三角形． ５分!!!!!!!!!!! 在 Ｒｔ△ＡＢＣ中：设 ＡＣ＝ｘ，则 ＡＢ＝２ｘ，由勾股定理， 得 ｘ２ ＋（ 槡４ ３）２ ＝（２ｘ）２， 解得 ｘ＝４，∴ＡＣ＝４，ＡＢ＝８． ８分!!!!!!!!!! 设 ＡＤ＝ｍ，则 ＤＦ＝ＢＦ＝３ｍ， 由 ＡＢ＝ＡＤ＋２ＤＦ＝ｍ＋６ｍ＝８，得 ｍ＝８ ７， ∴⊙Ｏ的直径 ＝２ＡＤ＝１６ ７． １０分!!!!!!!!!! ２４．解：（１）∵四边形 ＡＢＣＤ与四边形 ＡＥＦＧ是正方形， ∴ＡＤ＝ＡＢ，∠ＤＡＧ＝∠ＢＡＥ＝９０°，ＡＧ＝ＡＥ， ∴△ＡＤＧ≌△ＡＢＥ， ∴∠ＡＧＤ＝∠ＡＥＢ． ２分!!!!!!!!!!!!!! 第 ２４题解图① 如解图 ①，延长 ＥＢ交 ＤＧ于 点 Ｈ， ∵ 在 △ＡＤＧ 中，∠ＡＧＤ ＋ ∠ＡＤＧ＝９０°， ∴∠ＡＥＢ＋∠ＡＤＧ＝９０°． ∵ 在 △ＤＥＨ 中， ∠ＡＥＢ ＋ ∠ＡＤＧ＋∠ＤＨＥ＝１８０°， ∴∠ＤＨＥ ＝９０°． ∴ＤＧ⊥ＢＥ； ５分!!!!!!!!!!!!!!!!! （２）∵四边形 ＡＢＣＤ与四边形 ＡＥＦＧ是正方形， ∴ＡＤ＝ＡＢ，∠ＤＡＢ＝∠ＧＡＥ＝９０°，ＡＧ＝ＡＥ． ∴∠ＤＡＢ＋∠ＢＡＧ＝∠ＧＡＥ＋∠ＢＡＧ． ∴∠ＤＡＧ＝∠ＢＡＥ． ∵ＡＤ＝ＡＢ，∠ＤＡＧ＝∠ＢＡＥ，ＡＧ＝ＡＥ， ∴△ＡＤＧ≌△ＡＢＥ（ＳＡＳ）． ∴ＤＧ＝ＢＥ． ７分!!!!!!!!!!!!!!!!! 第 ２４题解图② 如解图②，过点 Ａ作 ＡＭ⊥ＤＧ 交 ＤＧ于点 Ｍ， ∠ＡＭＤ＝∠ＡＭＧ＝９０°， ∵ＢＤ是 正 方 形 ＡＢＣＤ的 对 角线， ∴∠ＭＤＡ＝∠ＭＢＡ＝∠ＭＡＢ ＝４５°，ＢＤ＝２． ∴ＡＭ＝１ ２ＢＤ＝１． 在 Ｒｔ△ＡＭＧ中， ∵ＡＭ２ ＋ＧＭ２ ＝ＡＧ２， ∴ＧＭ＝２． ∵ＤＧ＝ＤＭ＋ＧＭ＝１＋２＝３， ∴ＢＥ＝ＤＧ＝３． １２分!!!!!!!!!!!!!!! ２５．解：（１）①由题知： ａ＋ｂ＋３＝０ ４ａ－２ｂ{ ＋３＝３ ， 解得： ａ＝－１ ｂ{ ＝－２ ． ∴该抛物线解析式为：ｙ＝－ｘ２ －２ｘ＋３； ３分!!!!! ②记过点 Ｐ作 ｘ轴的垂线与线段 ＢＣ交于点 Ｄ， 设直线 ＡＢ的解析式为：ｙ＝ｋｘ＋ｎ，则 ｋ＋ｎ＝０ －２ｋ＋ｎ{ ＝３ ， 解得 ｋ＝－１ ｎ{ ＝１ ． ∴直线 ＡＢ的解析式为 ｙ＝－ｘ＋１． ５分!!!!!!! 设 Ｐ（ｍ，－ｍ２ －２ｍ＋３），Ｄ（ｍ，－ｍ＋１）， ∴ＰＤ ＝（－ｍ２ －２ｍ＋３）－（－ｍ＋１） ＝－ｍ２ －ｍ＋２． ∴Ｓ＝１ ２（－ｍ２ －ｍ＋２）（ｘＢ －ｘＡ） ＝－３ ２ｍ２ －３ ２ｍ＋３（－２＜ｍ＜１） ＝－３ ２（ｍ＋１ ２）２ ＋１５ ４， ∴当 ｍ＝－１ ２时，△ＰＡＢ的面积有最大值． ∴Ｐ（－１ ２，１５ ４）； ８分!!!!!!!!!!!!!!! （２）∵抛物线 ｙ＝ａｘ２ ＋ｂｘ＋３（ａ≠０）经过点 Ａ（－２，３）， ∴ｂ＝２ａ． ∴ｙ＝ａｘ２ ＋２ａｘ＋３． ∴对称轴为直线 ｘ＝－１， （Ⅰ）当 ａ＜０时，由 ｙ＝ａｘ２＋２ａｘ＋３ ｙ＝－ｘ{ ＋１ 得 ａｘ２ ＋（２ａ＋１）ｘ＋２ ＝０， （ｘ＋２）（ａｘ＋１）＝０， ∴ｘ１ ＝－２，ｘ２ ＝－１ ａ． ∴当 ０≤ －１ ａ≤１时，满足条件， ∴ａ≤ －１； １１分!!!!!!!!!!!!!!!!! （Ⅱ）当 ａ＞０时，由 ｙ＝ａｘ２＋２ａｘ＋３ ｙ＝－ｘ{ ＋１ 得 ａｘ２ ＋（２ａ＋１）ｘ＋２ ＝０， ∴Δ＝（２ａ－１）２ ＞０， ∴ａ≠ １ ２， １３分!!!!!!!!!!!!!!!!! 综上所述，满足条件的 ａ的值为 ａ≤ －１或 ａ＞０且 ａ≠ １ ２． １４分                                                                    !!!!!!!!!!!!!!!!!!!! ９１ ２０１８－２０１９学年上学期期末三明市初中毕业班质量检测 数学试卷参考答案及评分标准 一、选择题（每题 ４分，共 ４０分） １．Ｃ　２．Ｂ　３．Ｃ　４．Ｂ　５．Ｃ　６．Ａ　７．Ｄ　８．Ｄ　９．Ａ　 １０．Ｂ 二、填空题（每题 ４分，共 ２４分） １１．ｘ＝±３　１２．５ ３　１３．８　１４．－６　１５．（３，３） １６． 槡２ １０（写成 槡４０不扣分） 三、解答题（共 ８６分） １７．解：依题意得 Δ＝０，即： ４－４（ｍ２ －ｍ）＝０ ４分!!!!!!!!!!!!!! ∴ｍ２ －ｍ－１＝０． 解得 ｍ１ ＝ 槡１＋ ５ ２ ，ｍ２ ＝ 槡１－ ５ ２ ． ８分!!!!!!!!!! １８．解：（Ⅰ） （Ⅱ） 正确画出主视图得 ２分，正确画出俯视图得 ３分，正确画出 左视图得 ３分． １９．解：（１）设袋子中白球有 ｘ个，则 ｘ １＋ｘ＝２ ３， ２分!!!! 解得 ｘ＝２， 经检验 ｘ＝２是该分式方程的解， ∴袋子中白球有 ２个； ４分!!!!!!!!!!!!! （２）列表如下： 红 白 １ 白 ２ 红 （红，红） （红，白 １） （红，白 ２） 白 １ （白 １，红） （白 １，白 １） （白 １，白 ２） 白 ２ （白 ２，红） （白 ２，白 １） （白 ２，白 ２） ６分!!!!!!!!!!!!!!!!!!!!!! 由表格可知，共有 ９种等可能结果，其中两次都摸到白球的 结果有 ４种， 所以 Ｐ（两次都摸到白球）＝４ ９ ． ８分!!!!!!!! ２０．解：（１）∵ＣＤ⊥ＡＢ，ＢＥ⊥ＡＢ， ∴∠ＣＤＡ＝∠ＥＢＤ＝９０°， ∴ＣＤ∥ＢＥ． １分!!!!!!!!!!!!!!!!! 又 ∵ＢＥ＝ＣＤ， ∴四边形 ＣＤＢＥ为平行四边形． ３分!!!!!!!!! 又∵∠ＥＢＤ＝９０°， ∴四边形 ＣＤＢＥ为矩形． ４分!!!!!!!!!!!! （２）∵∠ＡＣＢ＝９０°，∠ＡＢＣ＝３０°， ∴ＡＢ＝２ＡＣ＝４． ∴ＢＣ＝ ＡＢ２ －ＡＣ槡 ２ 槡＝２ ３． ６分!!!!!!!!!!! ∵四边形 ＣＤＢＥ为矩形， ∴ＤＥ＝ＢＣ 槡＝２ ３． ８分!!!!!!!!!!!!!! ２１．解：（１）作图如解图； ４分!!!!!!!!!!!!!! 第 ２１题解图 （２）∵△ＡＣＤ∽△ＡＢＣ， ∴ＡＤ ＡＣ＝ＡＣ ＡＢ． ６分!!!!!!!!!!!!!!!!! ∵ＡＢ＝８，ＡＣ＝６， ∴ＡＤ ６ ＝６ ８． ∴ＡＤ＝９ ２． ８分!!!!!!!!!!!!!!!!! ２２．解：（１）设每件童装降价 ｘ元，则： （４０－ｘ）（２ｘ＋２０）＝１２００． ２分!!!!!!!!!!! 解得：ｘ１ ＝２０，ｘ２ ＝１０． ４分!!!!!!!!!!!!! 为使顾客得到更多实惠，∴ｘ＝２０． 答：每件童装应降价 ２０元． ５分!!!!!!!!!!! （２）设每件童装降价 ｘ元时，一天销售利润为 ｙ元，则： ｙ＝（４０－ｘ）（２ｘ＋２０） ＝－２ｘ２ ＋６０ｘ＋８００ ＝－２（ｘ－１５）２ ＋１２５０， ８分!!!!!!!!!!!! ∵ －２＜０， ∴当 ｘ＝１５时，ｙ有最大值，最大值为 １２５０． 答：当每件童装降价 １５元时，这种童装一天的销售利润最 多，最多利润是 １２５０元． １０分!!!!!!!!!!! ２３．（１）∵Ｄ（３，３）在双曲线 ｙ＝ｋ ｘ（ｘ＞０）上， ∴ ｋ＝３×３＝９； ３分!!!!!!!!!!!!!!! （２）如解图，作 ＤＦ⊥ｘ轴，垂足为 Ｆ，作 ＢＥ⊥ｘ轴，垂足为 Ｅ ，连接 ＡＣ， 第 ２３题解图 ∵四边形 ＡＢＣＤ为正方形， ∴ＡＢ＝ＡＤ，∠ＢＡＤ＝９０°． ∴∠ＢＡＥ＋∠ＤＡＦ＝９０°． 又∵ＢＥ⊥ＡＥ， ∴∠ＢＡＥ＋∠ＡＢＥ＝９０°． ∴∠ＤＡＦ＝∠ＡＢＥ． 又∵∠ＤＦＡ＝∠ＡＥＢ＝９０°，ＡＤ＝ＡＢ， ∴△ＡＦＤ≌△ＢＥＡ（ＡＡＳ）． ∴ＡＦ＝ＢＥ，ＤＦ＝ＥＡ． ４分!!!!!!!!!!!!! 设 Ａ（ａ，０），则 ＯＡ＝ａ                                                                    ， ０２ 又∵Ｄ（３，３）， ∴ＤＦ＝３，ＯＦ＝３，ＡＦ＝３－ａ． ∴ＢＥ＝ＡＦ＝３－ａ，ＥＡ＝ＤＦ＝３． ∴ＥＯ＝３－ａ． ∵点 Ｂ在第二象限， ∴Ｂ点坐标为（ａ－３，３－ａ）． ６分!!!!!!!!!! 又∵点 Ｂ在双曲线 ｙ＝－４ ｘ（ｘ＜０）上， ∴（ａ－３）（３－ａ）＝－４． ∴ａ１ ＝１，ａ２ ＝５． ∵点 Ｂ在第二象限， ∴ａ＝１， ∴点 Ａ坐标为（１，０）． ７分!!!!!!!!!!!!! ∴ＯＡ＝１，ＡＦ＝２． ∴ＡＤ＝ ＡＦ２ ＋ＤＦ槡 ２ 槡＝ １３． ∴ＡＣ 槡＝ ２ＡＤ 槡＝ ２６． ９分!!!!!!!!!!!!! ∴ＯＣ＝ ＡＣ２ －ＯＡ槡 ２ ＝５． ∴Ｃ（０，５）． １０分!!!!!!!!!!!!!!!!! ２４．解：（１）∵四边形 ＡＢＣＤ与四边形 ＣＥＦＧ都是矩形， ∴∠ＡＢＣ＝∠ＦＧＣ＝９０°． ∴ＡＢ∥ＦＧ，ＡＣ＝ ＡＢ２ ＋ＢＣ槡 ２ ＝５． ２分!!!!!!!! ∴ＡＦ ＢＧ＝ＣＦ ＣＧ＝ＡＣ ＢＣ＝５ ４； ４分!!!!!!!!!!!!! 第 ２４题解图 （２）（Ⅰ）如解图，连接 ＣＦ，在图① 中有ＣＦ ＣＧ＝ＡＣ ＢＣ＝５ ４， 由旋转可得：∠ＢＣＧ＝∠ＡＣＦ， ６分!!!!!!!!! ∴△ＢＣＧ∽△ＡＣＦ． ∴ＡＦ ＢＧ＝ＡＣ ＢＣ＝５ ４． ８分!!!!!!!!!!!!!!! （Ⅱ）ＣＰ⊥ＡＦ． ９分!!!!!!!!!!!!!!!! 理由：如解图，记 ＡＦ与 ＣＧ相交于点 Ｍ，由（Ⅰ）知：△ＢＣＧ ∽△ＡＣＦ， ∴∠ＡＦＣ＝∠ＢＧＣ． 又∵∠ＣＭＦ＝∠ＰＭＧ， ∴△ＣＭＦ∽△ＰＭＧ． １０分!!!!!!!!!!!!! ∴ＣＭ ＰＭ＝ＭＦ ＭＧ． 又∵∠ＣＭＰ＝∠ＦＭＧ． ∴△ＣＭＰ∽△ＦＭＧ． １１分!!!!!!!!!!!!! ∴∠ＣＰＭ＝∠ＦＧＭ＝９０°． ∴ＣＰ⊥ＡＦ． １２分!!!!!!!!!!!!!!!!! ２５．（１）证明：抛物线 ｙ１ ＝ａ（ｘ－ｈ）２ ＋２的顶点坐标为（ｈ，２）， ２分!!!!!!!!!!!!!!!!!!!!!!! ∵当 ｘ＝ｈ时，ｙ２ ＝ｋｈ－ｋｈ＋２＝２， ∴直线 ｌ恒过抛物线 Ｃ的顶点； ４分!!!!!!!!! （２）解：∵ｈ＝１． ∴顶点坐标为（１，２）． ∵当 ｔ≤ｘ≤ｔ＋３时，二次函数 ｙ１ ＝ａ（ｘ－１）２ ＋２的最小值 为 ２， ∴ｔ≤１≤ｔ＋３． ∴ －２≤ｔ≤１． ９分!!!!!!!!!!!!!!!! （３）解：方法一： ∵线段 ＰＱ（不含端点 Ｐ，Ｑ）上至少存在一个横坐标为整数 的点， ① 若 ａ＞０， 则 ｘ＝ｈ＋１时，有 ｙ２ ＞ｙ１， ∴ｋ（ｈ＋１）－ｋｈ＋２＞ａ（ｈ＋１－ｈ）２ ＋２． ∴ａ＜ｋ． ∵１≤ｋ≤３， ∴０＜ａ＜１． １２分!!!!!!!!!!!!!!!!! ② 若 ａ＜０， 则 ｘ＝ｈ－１时，有 ｙ２ ＜ｙ１， ∴ｋ（ｈ－１）－ｋｈ＋２＜ａ（ｈ－１－ｈ）２ ＋２， ∴ａ＞－ｋ． ∵１≤ｋ≤３， ∴ －３≤ －ｋ≤ －１， ∴ －１＜ａ＜０． 综上所述，ａ的取值范围是 ０＜ａ＜１或 －１＜ａ＜０． １４分 !!! !!!!!!!!!!!!!!!!!!!! 方法二： ∵Ｑ为抛物线与直线 ｌ的另一个交点， 由 ｙ１ ＝ｙ２ 得：ａ（ｘ－ｈ）２ ＋２＝ｋｘ－ｋｈ＋２， 解得 ｘ１ ＝ｈ，ｘ２ ＝ｈ＋ｋ ａ． ∵直线 ｌ恒过抛物线 Ｃ的顶点（ｈ，２）， ∴Ｑ的横坐标为 ｈ＋ｋ ａ． ①当 ａ＞０时，ｈ＋ｋ ａ－ｈ＞１， ∴ａ＜ｋ． ∵１≤ｋ≤３， ∴０＜ａ＜１． １２分!!!!!!!!!!!!!!!!! ②当 ａ＜０时，ｈ－（ｈ＋ｋ ａ）＞１， ∴ａ＞－ｋ． ∵１≤ｋ≤３， ∴ －３≤ －ｋ≤ －１． ∴ －１＜ａ＜０． 综上所述，ａ的取值范围是 ０＜ａ＜１或 －１＜ａ＜０． １４分 !!!                                                                        !!!!!!!!!!!!!!!!!!!! １２ 南平市 ２０１８－２０１９学年第一学期九年级期末 质量检测数学试题参考答案及评分说明 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分） １．Ｃ　２．Ｂ　３．Ｃ　４．Ｄ　５．Ｄ　６．Ａ　７．Ｃ ８．Ｂ　９．Ａ　１０．Ｂ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．ｘ 槡＝± ２　１２．０．３　１３．１　１４．３　１５．±２ １６．１９．５ 三、解答题（本大题共 ９小题，共 ８６分） １７．（１）解：ｘ２ －２ｘ＝０． １分!!!!!!!!!!!!!! ｘ（ｘ－２）＝０． ２分!!!!!!!!!!!!! ｘ１ ＝０，ｘ２ ＝２． ４分!!!!!!!!!!!!! （２）解：∵ａ＝１，ｂ＝－５，ｃ＝－５， １分!!!!!!!!! ｘ＝５± （－５）２槡 ＋４×５ ２ ２分!!!!!!!!! ｘ＝ 槡５±３ ５ ２ ， ｘ１ ＝ 槡５＋３ ５ ２ ，ｘ２ ＝ 槡５－３ ５ ２ ． ４分!!!!!!!! １８．解：∵一元二次方程 ｘ２ ＋３ｘ＋ｍ＝０有两个不相等的实 数根， ∴Δ＝３２ －４ｍ＞０， ４分!!!!!!!!!!!!!! ∴ｍ＜９ ４， ６分!!!!!!!!!!!!!!!!!! ∵ｍ为正整数， ∴ｍ＝１或 ｍ＝２． ８分!!!!!!!!!!!!!!! １９．解：（１）食堂早餐的食品一共有 ８种不同的可能． ２分! （２）方法一：画树状图如解图： 第 １９题解图 ６分!!!!!!!!!!!!!!!!!!!!!! ∴（肉包，牛奶）（肉包，豆浆）（馒头，牛奶）（馒头，豆浆） （鸡蛋，牛奶）（鸡蛋，豆浆）（油饼，牛奶）（油饼，豆浆）， ８分!!!!!!!!!!!!!!!!!!!!! 由树状图可知，共 ８种等可能的情况，其中刚好得到牛奶 和馒头的情况有 １种． ∴Ｐ（得到牛奶和馒头）＝１ ８． ８分!!!!!!!!!! 方法二：列表如下： 窗口一 窗口二 牛奶 豆浆 肉包 （肉包，牛奶） （肉包，豆浆） 馒头 （馒头，牛奶） （馒头，豆浆） 鸡蛋 （鸡蛋，牛奶） （鸡蛋，豆浆） 油饼 （油饼，牛奶） （油饼，豆浆） ７分!!!!!!!!!!!!!!!!!!!!!! 由列表可知，共 ８种等可能的情况，其中刚好得到牛奶和 馒头的情况有 １种． ∴Ｐ（得到牛奶和馒头）＝１ ８． ８分!!!!!!!!!! ２０．（１）解：作图如解图； ３分!!!!!!!!!!!!! 第 ２０题解图 （２）证明：∵ＰＣ平分∠ＡＰＢ，∠ＡＰＢ＝１２０°， ∴∠ＡＰＣ＝∠ＣＰＢ＝６０°， ４分!!!!!!!!!!!! ∵∠ＡＢＣ与∠ＡＰＣ同对弧 ＡＣ， ∴∠ＡＢＣ＝∠ＡＰＣ＝６０° ５分!!!!!!!!!!!! ∵∠ＣＡＢ与∠ＣＰＢ同对弧 ＢＣ ∴∠ＣＡＢ＝∠ＣＰＢ＝６０°， ６分!!!!!!!!!!!! ∴∠ＡＣＢ＝１８０°－∠ＡＢＣ－∠ＣＡＢ＝６０°， ∴∠ＡＣＢ＝∠ＡＢＣ＝∠ＣＡＢ＝６０°， ７分!!!!!!!! ∴△ＡＢＣ是等边三角形． ８分!!!!!!!!!!!! ２１．解：（１）∵Ｓ＝ｘ（４８－ｘ） ３ ， ２分!!!!!!!!!!!! ∴Ｓ＝－１ ３ｘ２ ＋１６ｘ（０＜ｘ≤２０）； ３分!!!!!!!! （２）花园面积可以达到 １８０平方米， ４分!!!!!!! ∵ －１ ３ｘ２ ＋１６ｘ＝１８０， ５分!!!!!!!!!!!!! ∴ｘ１ ＝１８，ｘ２ ＝３０， ６分!!!!!!!!!!!!!! ∵院墙的最大长度为 ２０ｍ， ∴ｘ２ ＝３０（不符合题意舍去）， ∴ｘ＝１８． ７分!!!!!!!!!!!!!!!!!! 答：当花园长为 １８ｍ，宽为 １０ｍ时，花园面积可以达到 １８０ ｍ２． ８分!!!!!!!!!!!!!!!!!!!! 第 ２２题解图 ２２．解：如解图，连接 ＨＢ， ∵ＡＥ⊥ＥＯ， ∴∠ＡＥＯ＝９０°， ∵△ＡＥＯ绕点 Ｏ顺时针 旋转得到△ＤＨＯ， ∴△ＡＥＯ≌△ＤＨＯ， ∴∠Ａ＝∠Ｄ， ∠ＤＨＯ＝∠ＡＥＯ＝９０°， ∠ＤＯＨ＝∠ＡＯＥ， ３分!!!!!!!!!!!!!!! ∵Ｄ，Ｈ，Ｂ在一条直线上， ∴ＯＨ⊥ＤＢ， 解法一：∵ＯＤ＝ＯＢ， ∴∠Ｂ＝∠Ｄ， ４分!!!!!!!!!!!!!!!! ∴∠Ａ＝∠Ｂ， ５分!!!!!!!!!!!!!!!! ∵∠ＡＯＥ与∠Ｂ同对弧 ＡＤ， ∴∠ＡＯＥ＝２∠Ｂ                                                                    ， ２２ ∴∠ＡＯＥ＝２∠Ａ， ７分!!!!!!!!!!!!!!! 在 Ｒｔ△ＡＯＥ中，∠ＡＯＥ＋∠Ａ＝９０°， ∴２∠Ａ＋∠Ａ＝９０°， ８分!!!!!!!!!!!!!! ∴∠Ａ＝３０°， ９分!!!!!!!!!!!!!!!!! ∴∠ＡＯＥ＝６０°即 α＝６０°． １０分!!!!!!!!!!! 解法二：∵ＯＤ＝ＯＢ，ＯＨ⊥ＤＢ， ∴ＯＨ平分∠ＢＯＤ即∠ＢＯＨ＝∠ＤＯＨ， ７分!!!!!! ∵∠ＤＯＨ＝∠ＡＯＥ， ∴∠ＤＯＨ＝∠ＡＯＥ＝∠ＢＯＨ＝６０°， ９分!!!!!!! ∴α＝６０°． １０分!!!!!!!!!!!!!!!!! 第 ２３题解图 ２３．解：（１）如解图，过点 Ａ作 ＡＢ⊥ｘ 轴，垂足为 Ｂ， １分!!!!!! ∵ 直 线 与 ｙ轴 正 半 轴 的 夹 角 为 ６０°， ∴∠ＡＯＢ＝３０°， ２分!!!!! ∴ＡＢ＝１ ２ＯＡ＝１， ３分!!!!! ∴在 Ｒｔ△ＡＯＢ中， ＯＢ＝ ＯＡ２ －ＡＢ槡 ２ ＝ ２２ －１槡 ２ 槡＝ ３， ４分!!!!!!! ∴Ａ（ 槡－ ３，１）， ５分!!!!!!!!!!!!!!!! ∴ｍ 槡＝－ ３， ６分!!!!!!!!!!!!!!!!! ∴反比例函数的解析式为 ｙ＝－槡３ ｘ； ７分!!!!!!! （２） 槡－ ３＜ｘ＜０． １０分!!!!!!!!!!!!!! ２４．解：（１）方法一：如解图①，作 ＡＧ⊥ＢＣ于 Ｇ点，延长 ＦＥ交 ＡＧ于 Ｈ点， ∵ＡＢ＝ＡＣ， ∴∠ＢＡＧ＝３０°， １分!!!!!!!!!!!!!!! ∵ＥＢ绕点 Ｅ顺时针旋转 ６０°得到线段 ＥＦ， ∴∠ＢＥＦ＝６０°， ∴∠ＢＥＦ＝∠Ｂ， ∴ＥＦ∥ＢＣ， ２分!!!!!!!!!!!!!!!!! ∵ＡＧ⊥ＢＣ， ∴ＡＧ⊥ＦＨ， ３分!!!!!!!!!!!!!!!!! 在 Ｒｔ△ＡＥＨ中，∵ＡＥ＝６，∠ＥＡＨ＝３０°， ∴ＥＨ＝１ ２ＡＥ＝３，ＡＨ＝ ＡＥ２ －ＥＨ槡 ２ 槡＝３ ３， 在 Ｒｔ△ＡＦＨ中， ＡＦ＝ ＡＨ２ ＋ＦＨ槡 ２ ＝ （ 槡３ ３）２ ＋５槡 ２ 槡＝２ １３． ４分!!! 方法二：如解图②，连接 ＦＢ，作 ＦＰ⊥ＡＢ于 Ｐ点， ∵ＥＢ绕点 Ｅ顺时针旋转 ６０°得到线段 ＥＦ， ∴△ＥＢＦ是等边三角形， １分!!!!!!!!!!! 又∵ＦＰ⊥ＡＢ，∴∠ＥＦＰ＝３０°， ∴ＥＰ＝１ ２ＥＦ＝１， ２分!!!!!!!!!!!!!! ∴ＡＰ＝７， 在 Ｒｔ△ＥＦＰ中，ＰＦ＝ ＥＦ２ －ＥＰ槡 ２ 槡＝ ３． ３分!!!!! 在 Ｒｔ△ＡＰＦ中，ＡＦ＝ ＦＰ２ ＋ＡＰ槡 ２ ＝ （槡３）２ ＋７槡 ２ 槡＝２１３． ４分!!!!!!!!!!!!!!!!!!!!! （２）①如解图③，连接 ＦＢ， ∵ＥＢ绕点 Ｅ顺时针旋转 ６０°得到线段 ＥＦ， ∴△ＥＢＦ是等边三角形， ∴ＦＢ＝ＥＢ，∴∠ＦＢＥ＝∠ＡＢＣ＝６０°， ６分!!!!!!! ∴∠ＦＢＥ＋∠ＥＢＡ＝∠ＡＢＣ＋∠ＥＢＡ， 即∠ＦＢＡ＝∠ＥＢＣ， ７分!!!!!!!!!!!!!! 又∵ＡＢ＝ＢＣ， ∴△ＦＢＡ≌△ＥＢＣ， ８分!!!!!!!!!!!!!! ∴ＡＦ＝ＣＥ， ９分!!!!!!!!!!!!!!!!! ② 槡４ ３－２≤ＡＦ≤ 槡４ ３＋２． １２分!!!!!!!!!! ∵ＤＥ＝２， ∴Ｅ点在以 Ｄ为圆心，半径为 ２的圆上，且 槡４ ３－２≤ＣＥ≤ 槡４ ３＋２． ∵ＡＦ＝ＣＥ， 槡∴４ ３－２≤ＡＦ≤ 槡４ ３＋２．（回答合理均得分） 第 ２４题解图③ ２５．解：（１）依题意可得 ｙ１ ＝－１ ３ｘ２ ＋ｂｘ， １分!!!!!! ∵ｙ１ 顶点在直线 ｘ＝２上， ∴ － ｂ ２×（－１ ３） ＝２， ∴ｂ＝４ ３， ２分!!!!!!!!!!!!!!!!!!!! ∴ｙ１ ＝－１ ３ｘ２ ＋４ ３ｘ． ３分!!!!!!!!!!!!!!! （２）方法一：如解图①，设直线 ＰＱ与直线 ｘ＝２相交与 Ｅ点， ∴ＰＥ＝ＰＱ ２， ４分!!!!!!!!!!!!!!!!!!! ∵１＜ＰＱ≤２，∴ １ ２ ＜ＰＥ≤１， ５分!!!!!!!!!!!! ∴当 ＰＥ＝１ ２时，ｘρ＝２－１ ２ ＝３ ２，ｙρ＝５ ４， ６分!!!!!! 当 ＰＥ＝１时，ｘρ＝２－１＝１，ｙρ＝１， ７分!!!!!!!!!! ∴１≤ｔ＜５ ４． ９分!!!!!!!!!!!!!!!!!! 方法二：设 －１ ３ｘ２ ＋４ ３ｘ＝ｔ， ∴（ｘ－２）２ ＝－３ｔ＋４                                                                        ， ３２ ∴ｘ１ ＝ ４－３槡 ｔ＋２，ｘ２ ＝－ ４－３槡 ｔ＋２， ５分!!!!!!!! ∴ＰＱ＝ｘ１ －ｘ２ ＝２ ４－３槡 ｔ， ６分!!!!!!!!!!!! ∴ＰＱ＝１时，４－３ｔ＝１ ４，ｔ＝５ ４， ＰＱ＝２时，４－３ｔ＝１，ｔ＝１， ８分!!!!!!!!!!!!! ∴１≤ｔ＜５ ４． ９分!!!!!!!!!!!!!!!!!! 第 ２５题解图① （３）如解图②，设直线 ｙ＝１与 ｙ１ 依次相交 Ｍ１，Ｎ１ 于两点， 由（２）可得 Ｍ１Ｎ１ 槡＝２ ４－３×１＝２， ｘＭ１ 槡＝－ ４－３×１＋２＝１， ∴Ｍ１（１，１）， １０分!!!!!!!!!!!!!!!!!! 由平移的性质可得 ＭＮ＝Ｍ１Ｎ１ ＝２，Ｍ（ 槡２＋ ３，１）， １１分!!! ∴根据勾股定理可得 ＭＡ＝ （ 槡２＋ ３－２）２ ＋１槡 ２ ＝２， １２分! 证法一：∵ＭＡ＝ＭＮ＝２， ∴∠ＭＡＮ＝∠ＭＮＡ． １３分!!!!!!!!!!!!!!! ∵ＭＮ∥ＣＤ， ∴∠ＭＮＡ＝∠ＮＡＤ， ∴射线 ＡＮ平分∠ＭＡＤ． １４分!!!!!!!!!!!!! 证法二：如解图②，过 Ｎ点作 ＮＰ⊥ＡＭ 于点 Ｐ，ＮＱ⊥ＣＤ于 点 Ｑ， ∴ＮＱ＝１， ∵Ｓ△ＡＭＮ ＝１ ２ＡＭ·ＮＰ＝１ ２ＭＮ·１， ∴ＮＰ＝１， １３分!!!!!!!!!!!!!!!!!!! ∴ＮＰ＝ＮＱ， ∵ＮＰ⊥ＡＭ于 Ｐ点，ＮＱ⊥ＣＤ， ∴射线 ＡＮ平分∠ＭＡＤ． １４分!!!!!!!!!!!!! 第 ２５题解图②                            ４２